Equilibrium Relationships
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Mass Transfer Coefficients
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today we're discussing mass transfer coefficients, which are crucial for understanding how substances move across interfaces, like from water to air. Can anyone tell me why these coefficients are important?

They show how easily substances can transfer from one phase to another!

Exactly! They tell us about the resistance to mass transfer. We often denote these coefficients as k₁ for liquid and k₂ for gas. Remembering them can be easier with a mnemonic: 'K Goes Global' - K for coefficient, G for gas, and L for liquid. Can anyone repeat that?

K Goes Global!

Great! Now, who can explain how mass transfer occurs at an interface?
Understanding Flux and Concentration Gradient
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

To quantify mass transfer, we use a concept called flux, which can be defined as the rate of mass transfer per unit area. What causes this flux?

It's caused by differences in concentration across the interface!

Correct! This concentration difference is our driving force. Think of it like a race—those with a higher concentration want to move to where there’s less. The equation for flux could be remembered as 'F Equals C Difference,' where C is the concentration gradient. Who can write that equation?

F = k(C₁ - C₂)!

Fantastic! Now, if we can't measure concentrations directly at the interface, what might we do?
Equilibrium Relationships and Henry's Law
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

When concentrations at the interface are hard to determine, we can invoke equilibrium relationships like Henry's Law. Does anyone know what Henry's Law states?

It relates the concentration of a gas in a liquid to its partial pressure above the liquid.

Right! It helps us find an assumed concentration that is in equilibrium with the bulk liquid. Can you express it mathematically?

C = k_H × P (where k_H is Henry's constant)!

Excellent! Remembering the relationships like 'Henry's Helps' can also be useful. Now, how do we solve for the concentration at the interface?
Mass Transfer Resistances in Series
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

We often model mass transfer resistances in series. Can someone explain what this means?

It means we add individual resistances from the two phases to find the total resistance to mass transfer!

That's right! Like in electrical circuits, these resistances add up, and the overall mass transfer resistance can be expressed as the sum of individual resistances. Just remember, 'Be the RESISTANT!' to help you recall that resistances build up. What analogy could we draw with other types of transfer?
Applications in Environmental Engineering
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

How do you think understanding mass transfer is crucial in environmental engineering?

It helps in assessing pollutants moving between air and water!

Correct! By understanding resistances and flux, we can design better systems for reducing pollutant transfer. Think of it as reducing the race conditions—slowing down chemical movement can protect water quality. Remember, 'Reduce-Race-Relations' in your tasks again!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section emphasizes the concepts surrounding mass transfer coefficients, the resistances experienced at phase boundaries, and how these concepts are pertinent for predicting fluxes across interfaces, particularly in environmental monitoring contexts. It introduces the notion of equilibrium relationships which can be used to relate concentrations in different phases.
Detailed
Detailed Summary
This section discusses the fundamental aspects of mass transfer in environmental contexts, particularly emphasizing the mass transfer coefficients associated with fluid interfaces, such as gas and liquid phases. The essential concept involves understanding the driving force for mass transfer, represented by concentration gradients. When mass transfer occurs from one phase to another—like water to air—there exists a resistance for mass transfer at the interface. This resistance can be expressed through mass transfer coefficients denoted as k₁ for the liquid phase and k₂ for the gas phase.
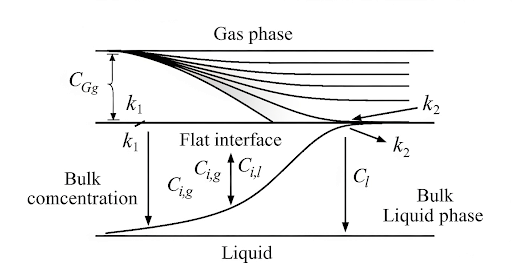
One of the challenges addressed is the estimation of concentrations at the interface, which are often unknown. The section proposes using equilibrium relationships, particularly Henry's law, to relate bulk concentrations to interface concentrations. By establishing a series of equations and resistance relationships, the section demonstrates how mass transfer can be modeled as a combination of resistances in series, thus enabling predictions of fluxes between phases. The implications of these concepts are significant for applications such as environmental quality monitoring, where understanding the limits and capabilities of mass transfer processes is critical.
Youtube Videos










Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Mass Transfer and Equilibrium
Chapter 1 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, we were discussing mass transfer across interfaces. We were discussing the general principles of mass transfer coefficient. So we defined something called as mass transfer coefficient and its dependency on the flow, the properties of the fluid and properties of the solute itself to some extent.
Detailed Explanation
This chunk introduces the concept of mass transfer and its relationship with two phases of matter, such as gas and liquid. The mass transfer coefficient is a crucial parameter that quantifies how effectively mass is transported from one phase to another. It depends on several factors, including the flow rate of fluids and the characteristics of the solute.
Examples & Analogies
Think about how a sugar cube dissolves in water. The mass transfer coefficient helps us understand how quickly the sugar particles move from the cube into the water. Factors like water temperature and how fast you stir (flow) will affect this process.
Gradient and Mass Transfer Resistance
Chapter 2 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If mass transfer is happening from water to air, the transfer of A is going from water to air, which means there is a gradient from water to air. So, we also discussed that close to the fluid interface, it is convenient for us to assume that there is a region of mass transfer resistance.
Detailed Explanation
This section explains that mass transfer occurs due to a concentration gradient between two phases. Near the interface, there exists a zone of resistance to mass transfer, meaning that the transfer is not instantaneous and some delay occurs. This resistance is critical to understanding how substances cross from one medium to another.
Examples & Analogies
Consider cooking pasta in boiling water. As the heat from the water tries to penetrate the pasta, the outer layer of pasta acts as a 'barrier,' slowing down the heat transfer. Similarly, in mass transfer, the area near the interface can slow down the movement of particles from one phase to another.
Introducing the Resistance in Series Model
Chapter 3 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So therefore, we cannot do this. So how do we work around this one? So we invoke what is called as a resistance in series approach to do this.
Detailed Explanation
When it is challenging to directly measure certain concentrations, the resistance in series approach comes into play. This method allows us to relate different concentrations through a series of resistances, effectively making it possible to account for the mass transfer occurring in different phases.
Examples & Analogies
Think about standing in line for a concert. Each person in front of you represents a step in a series of resistances to get to the front. Similarly, in the mass transfer model, each resistance (interface or phase) you encounter affects the overall time it takes for a substance to move from one phase to another.
Defining Mass Transfer Coefficients
Chapter 4 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, notice that this is small k, this is individual mass transfer coefficient. So, here what is k*? We know that A1 and A2 are in equilibrium.
Detailed Explanation
This chunk focuses on the specific mass transfer coefficients denoted by 'k'. These coefficients are essential since they describe the transfer rate of mass between the two phases. The equivalence of concentrations at equilibrium signifies that while they may be at the same state, it does not mean that mass transfer is at a standstill; it simply describes their relationship.
Examples & Analogies
Imagine a sponge soaked in water sitting on a table. The water will slowly transfer to air, and the rate at which this happens is influenced by the sponge's material (the mass transfer coefficient). Even though water is in equilibrium with air above it, the movement of water molecules from the sponge to the air continues at a certain rate, dictated by this coefficient.
Using Equilibrium Relationships
Chapter 5 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So what this means graphically is the following. I am going to draw this here. Henry’s constant is we are assuming its constant for this temperature, this is linear relationship.
Detailed Explanation
This part explains the graphical representation of equilibrium relationships, specifically mentioning Henry’s Law, which relates the concentration of a gas in a liquid to the pressure of that gas in the air above it. This relationship is typically linear, assuming the constant remains unchanged over a specific temperature range.
Examples & Analogies
An example of this can be seen in soft drinks. When a soda is bottled, the carbon dioxide gas is under pressure, and when you open it and the pressure decreases, the gas escapes (bubbles). The concentration of CO2 in the liquid decreases as it equilibrates with the lower pressure of CO2 in the air.
Overall Mass Transfer Resistance
Chapter 6 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So now you cross out all the n’s, now we get... This is a very useful representation.
Detailed Explanation
In this section, the overall mass transfer resistance is summarized in a formula that combines resistances from both phases. This formula allows us to determine which resistance dominates and thus controls the mass transfer process, making it crucial for engineering solutions.
Examples & Analogies
Think of traffic flow as an analogy. If a highway has one lane blocked but another highway has several open lanes, the flow on the blocked highway will determine how fast cars can travel overall, similar to dominating resistances in mass transfer that effects the overall rate of transport.
Key Concepts
-
Mass Transfer Coefficients: Important for assessing transfer rates between phases.
-
Flux: Defined as the mass transfer rate per unit area.
-
Resistances in Series: Total resistance impacts overall mass transfer rates.
-
Equilibrium Relationships: Used to estimate unknown concentrations at interfaces.
Examples & Applications
A lake polluted with a chemical highlights the significance of mass transfer, as contaminants can move between water and surrounding air.
Using Henry's Law, one can deduce the gas concentration in equilibrium with a given liquid concentration, which is essential in pollution studies.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Henry's law helps what we see, gas-to-liquid—concentration key!
Stories
Imagine a lake where fish and air mix, pollutants chase the air like eager fix. To halt their race, we measure with care, using coefficients, we avoid despair.
Memory Tools
‘K Goes Global’ reminds us, K for coeffs, Global for phases, easy to discuss.
Acronyms
R.E.S. - Resistances Exist in Series
Helps recall how total resistance works.
Flash Cards
Glossary
- Mass Transfer Coefficient
A proportionality constant that quantifies the mass transfer between phases.
- Flux
The rate of mass transfer per unit area.
- Equilibrium Relationship
A relationship that describes how concentrations in different phases relate under equilibrium conditions.
- Henry's Law
A law that relates the concentration of a gas in a liquid to its partial pressure.
- Resistances in Series
A concept stating that in mass transfer processes, total resistance is the sum of individual resistances.
Reference links
Supplementary resources to enhance your learning experience.
