Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Mass Transfer Coefficients
Unlock Audio Lesson

Let's discuss mass transfer coefficients, `kA12` and `kA21`. These coefficients help us understand the rate at which mass is transferred between phases. Why do you think these coefficients vary in different scenarios?

Is it because different surfaces have varying properties?

Exactly! Different surfaces like lakes or rivers have unique environmental conditions—velocity, temperature, and more. This brings us to choosing the correct correlation from our data sources.

So, we would need to look up the specific correlation that applies to our situation?

Right! It’s like consulting a reference book to find the right recipe for a dish based on available ingredients.
Calculating Flux
Unlock Audio Lesson

Now that we've discussed mass transfer coefficients, let's compute flux. Can anyone tell me what flux represents in environmental studies?

Flux is the rate at which a substance moves through a certain area, right?

Yes! And we can express this mathematically. What do you think happens to the flux if the concentration gradient increases?

It would increase too, I suppose?

Correct! This relationship—flux proportional to concentration gradient—is fundamental. Let's integrate that into our calculations.
Differential Equations and Concentration Over Time
Unlock Audio Lesson

To understand how concentration changes over time, we use a differential equation. Can anyone share why we need initial conditions for our calculations?

We start the calculations based on an initial concentration, right?

Absolutely! This starting point is critical for accurately predicting future concentrations. Let's visualize this function over time.

So the concentration will change in an exponential manner?

Good observation! It behaves like a first-order reaction, emphasizing the importance of understanding these processes.
Practical Applications and Risk Assessment
Unlock Audio Lesson

Let’s connect our theory to practice. If there's a chemical spill, what’s one of the first questions we should ask regarding the concentration of the pollutant in the water?

How long until it reaches a concentration that poses a risk to humans?

Exactly! We must continuously monitor those levels. This brings about the conversation on emergency response systems.

So, animals and plants can also be at risk from spills, right?

Yes, understanding the concentration and effects will guide us in assessing risks to all environmental factors.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, important concepts regarding the calculation of mass transfer coefficients, flux, and concentration over time in environmental systems are explored. The significance of choosing the appropriate correlations based on specific situations, such as evaporation from lakes, is emphasized.
Detailed
Calculating Flux and Concentration
This section details critical methodologies for calculating mass transport phenomena in environmental contexts, specifically focusing on flux and concentration. It begins with the definition of mass transfer coefficients, kA12 and kA21, which need to be derived based on various environmental conditions. The calculations rely heavily on empirical correlations available in literature, which vary depending on the type of scenario—be it evaporation from a lake, river, or ocean.
The section describes the process of determining these values by first collecting the relevant environmental data—like velocities of air and water, densities, viscosities, and diffusion coefficients. Once the coefficients are established, it transitions into applying them to a mass balance to derive a differential equation that captures the changing concentration of a substance over time.
Following this, the section describes the integration of this differential equation, allowing students to establish the concentration of a chemical as a function of time, highlighting practical applications such as assessing contamination levels in water or air after environmental incidents, exemplified by a spill of chemicals.
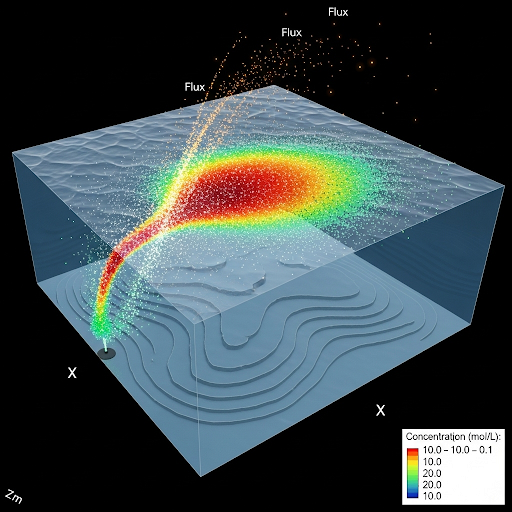
Significant emphasis is placed on understanding the implications of these calculations for public health and safety, establishing thresholds for hazardous concentrations in both aquatic environments and in the air. Finally, the section mentions the conservative nature of worst-case scenario modeling for effective emergency response stakeholders.
Youtube Videos










Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Mass Transfer Coefficients
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The mass transfer coefficients kA12 and kA21 are to be obtained from correlation. So, there are a variety of correlations that are available in literature. People have measured correlations for different scenarios.
Detailed Explanation
Mass transfer coefficients are key parameters in understanding how substances move between phases (like gas and liquid). kA12 refers to the transfer from phase 1 to phase 2, while kA21 is the transfer in the opposite direction. These coefficients are not fixed; instead, they rely on empirical data collected under various conditions (like different temperatures or fluid velocities). Researchers have documented these coefficients in correlation tables, which can guide calculations for specific environmental scenarios, such as evaporation from lakes or oceans.
Examples & Analogies
Consider cooking. When you boil water, the rate at which water evaporates into the air can be influenced by the temperature of the water (akin to kA). If you increase the heat, more water vapor escapes into the air, similar to how mass transfer coefficients work. Different cooking methods (like boiling versus simmering) offer varying correlations for evaporation, just as literature provides different correlations for various environmental conditions.
Selecting Appropriate Correlations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, you have to pick the correlation that is appropriate for your problem. For a lake, sometimes it will be lake mass transfer coefficient for a lake of a certain length, diameter, certain depth and all that.
Detailed Explanation
Selecting the correct mass transfer correlation is crucial for accurate calculations. Each environmental situation, like the size and type of a lake, can dramatically affect how substances evaporate. The characteristics of the lake—its depth, width, and even local weather conditions—need to be factored into the chosen correlation to ensure the results reflect real-life scenarios accurately.
Examples & Analogies
Imagine trying to measure how quickly a sponge absorbs water; a small sponge will absorb water at a different rate than a large sponge. Similarly, for lakes of different sizes, their ability to lose water to evaporation can vary, requiring different empirical correlations to predict accurately.
Estimating Concentration Over Time
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Once you do that, you go back to the calculate, estimate kA or kB, the overall coefficient...
Detailed Explanation
After determining the mass transfer coefficients, the next step involves calculating the concentration of a substance in a medium over time. This is performed using a differential equation that accounts for the change in concentration as a function of time. Essentially, as a substance evaporates or is transferred from one phase to another, its concentration changes. The calculations involve integrating this differential equation over specified time intervals.
Examples & Analogies
Think about a bathtub filled with water. If you drain water slowly, you can predict how much water will be left at a certain time using simple subtraction over time. In environmental contexts, understanding how pollutants in a lake dissipate over time can help in risk assessment and management just like monitoring water levels in a bathtub can help prevent overflow.
Impact of Initial Conditions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The initial concentration as a function of time must be determined, such as if M0 was dumped into the volume.
Detailed Explanation
Initial conditions play an essential role in calculating concentration changes over time. For instance, if a certain mass of a pollutant is introduced into a body of water, understanding this initial concentration is critical. These conditions serve as the starting point for tracking how concentration levels will change due to evaporation or chemical reactions, leading to a predicted time-based concentration profile.
Examples & Analogies
If a parent pours a glass of juice, the initial pour level represents the starting concentration of juice in that glass. As the juice is consumed, its concentration decreases. This analogy mirrors how pollutants decrease in concentration over time in environments like lakes or rivers.
Understanding First Order Reactions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This is like a first order reaction equation... So, we have this term here or this term here, we are seeing that the rate is the first order term.
Detailed Explanation
A first-order reaction in the context of mass transfer means the rate of change of concentration is directly proportional to the current concentration. In mass transfer scenarios, this concept simplifies our calculations, as it allows us to predict the change in concentration over time in a straightforward manner. Understanding the characteristics of first-order processes is fundamental to modeling environmental phenomena such as evaporation or biodegradation of substances.
Examples & Analogies
Consider how weeds grow in a garden. If you pull a few weeds today, the next day, the remaining weeds will continue to grow at a rate relative to how many are left. Similarly, the rate of pollutant decrease in water is proportional to how much remains, reflecting a first-order decay in concentration.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Mass Transfer Coefficients: Essential for quantifying mass transfer rates across phases.
-
Flux: Represents the movement rate of substances, influenced by gradients in concentration.
-
Differential Equations: Used to model concentration changes over time.
-
Concentration Changes: Important for understanding implications for environmental safety.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
If a chemical is spilled on a road, the concentration of the pollutant in the air can be estimated using mass transfer coefficients and surface conditions.
-
In assessing a lake's water quality post-spill, initial concentration can be derived from the volume of chemical spilled divided by the lake's surface area and volume.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Flux flows fast, through surfaces wide, concentration changes with the flow's tide.
📖 Fascinating Stories
-
Imagine a lake where a chemical is dumped; the concentrations rise, and nature is stumped. Monitoring daily keeps the wildlife safe, by calculating what's harmful, we can keep the pace.
🧠 Other Memory Gems
-
To remember the steps in calculating concentration: C = Co e^(-kt), where C starts as the initial and k is the rate!
🎯 Super Acronyms
MTC - Mass Transfer Coefficients
- Measure That Change in flow and concentrations!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Mass Transfer Coefficient
Definition:
A numerical value that quantifies the mass transfer rate per unit area and concentration gradient.
-
Term: Flux
Definition:
The rate of flow of a substance through a unit area.
-
Term: Concentration
Definition:
The amount of a substance in a given volume of solution.
-
Term: Differential Equation
Definition:
A mathematical equation that relates a function to its derivatives, used to model changing quantities over time.
-
Term: Evaporation
Definition:
The process by which liquid turns into vapor, often influenced by environmental conditions.
