Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Conservation Laws
Unlock Audio Lesson
Today we’ll start with an overview of conservation laws in fluid mechanics. Who can tell me what conservation laws are?
Are they principles that describe how certain quantities remain constant?
Exactly! There are three primary conservation laws we focus on: mass, momentum, and energy. Let’s first discuss mass conservation. Can anyone tell me what that entails?
It means the mass of a closed system remains constant over time?
Very good! This principle is fundamental when analyzing fluids. We can think of the mass entering a control volume and the mass exiting it. Now, how do we represent this mathematically?
Using the equation of continuity? The mass flow rates must be equal in and out?
Correct! Remember the acronym 'VMD'—Volume must equal Mass flow times Density. Let’s summarize before we move on. Mass remains constant!
Momentum Conservation
Unlock Audio Lesson
Now, let's move on to momentum conservation. Who can explain what this law suggests?
Is it that the total momentum of a closed system is constant unless acted on by an external force?
Absolutely! In fluids, this relates to forces like drag and lift. Can anyone provide an example of these forces in action?
Like when a plane takes off? The lift must overcome the gravitational force to gain altitude.
Exactly! And we also consider the relationship between net forces and acceleration. Let’s have a brief quiz. What is the equation relating force and momentum?
F equals the rate of change of momentum?
Right! F = dp/dt. Great job! Now let’s encapsulate this point: Momentum changes with external forces.
Energy Conservation
Unlock Audio Lesson
Now, who can define energy conservation for us?
Energy cannot be created or destroyed, right? It just changes forms?
Excellent! In fluid systems, this can be seen in pumps or turbines where mechanical energy is converted into fluid energy. What can cause energy loss in a system?
Friction losses? Or heat transfer?
Spot on! We must also remember that energy conservation helps us understand the efficiency of real-world systems. Who can summarize our discussion on energy conservation?
Energy remains constant, but it can be transformed or lost. We analyze these losses to improve system designs.
Perfect summary! Let’s wrap up this section by reiterating: all three laws are fundamental in understanding fluid behavior. They guide our analysis and decision-making.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section discusses the conservation laws of mass, momentum, and energy, elucidating their significance within fluid mechanics. It highlights how these laws govern fluid properties during motion and provides foundational concepts for solving real-world fluid dynamics problems.
Detailed
Detailed Summary of Basic Conservation Laws
This section dives into the foundational principles of fluid mechanics by discussing the three basic conservation laws: mass, momentum, and energy. These laws form the bedrock of fluid dynamics and dictate how fluids behave in various situations.
Mass Conservation
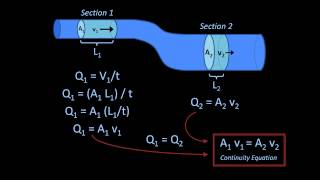
The law of mass conservation states that mass cannot be created or destroyed in an isolated system. In fluid dynamics, this is vital as it helps in determining the mass flow rate and how mass moves within a fluid system.
Momentum Conservation
Momentum conservation is anchored in Newton’s second law of motion. It dictates that the rate of change of momentum within a fluid system is equal to the sum of forces acting on it. This principle assists in solving problems involving forces, such as drag or lift on objects moving through a fluid.
Energy Conservation
Energy conservation, grounded in the first law of thermodynamics, indicates that the total energy within a closed system remains constant, although it can change forms. This law helps to assess energy transfers due to work done and heat exchange in fluid systems.
In application, these conservation laws are essential for analyzing and predicting the behavior of fluids under various conditions, especially when utilizing models like the Reynolds transport theorem.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Conservation of Mass
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, as you might have solved a lot of physics problems on solid body translations, rotations and all, the basic concept of linear momentum equations you apply, which is, you know, force is rate of change of momentum flux. That is the Newton’s second law of motion and you have been using that to solve many problems in twelfth level of the class in physics or fluid mechanics type of problems.
Now, when you consider a system that means these three conservation principles they are quite valid. When we consider an isolated system like, as I have given examples, the virtual fluid balls, they are isolated systems, okay? They can move at different times. Like, for example, if I consider a system of a set of fluid particles or a set of virtual fluid balls, as you can understand it, there is no change, no other type of mass decaying function is there. The mass will remain constant.
That means what will happen is mass at the system level at t is equal to mass at the system level at t will be the same, but they can have simple space at this location, but when it comes to t level they can fragment and they can occupy very complex surface at t times. So, mass conservation is a very simple thing. You just know it, the mass remains constant at t and t if you are considering an isolated system where you have n number of fluid particles or virtual fluid balls, that number will remain the same whether you have t time or t time.
Detailed Explanation
Conservation of mass is a fundamental principle in fluid mechanics. It states that for an isolated system, the total mass remains constant over time. This means that, even as the individual fluid particles move and change location, the overall mass of the system does not change. This principle is crucial when analyzing fluid flow in various systems, as it allows us to conclude that the mass entering a system must equal the mass leaving it, given that no mass is created or destroyed. Therefore, any calculations involving fluid dynamics often start with the assumption that mass conservation applies.
Examples & Analogies
Consider a balloon filled with air. If you were to squeeze the balloon, you would notice that the volume of the balloon changes, but the total amount of air inside it stays the same unless you let some air escape. This is a practical demonstration of mass conservation; no air is lost as you change the shape and size of the balloon.
Conservation of Momentum
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, as you might have solved a lot of physics problems on solid body translations, rotations and all, the basic concept of linear momentum equations you apply, which is, you know, force is rate of change of momentum flux. That is the Newton’s second law of motion and you have been using that to solve many problems in twelfth level of the class in physics or fluid mechanics type of problems.
Detailed Explanation
The conservation of momentum states that in an isolated system, the total momentum remains constant unless acted upon by an external force. In fluid mechanics, this is expressed mathematically via the momentum equations derived from Newton's second law, indicating that the change in momentum of fluid particles depends on the net force exerted on them. When analyzing fluid flows, we often calculate the net forces acting on a volume of fluid to determine how its motion changes over time. This concept is essential in designing systems where fluid motion is crucial, such as pipelines or nozzles.
Examples & Analogies
Think about a game of billiards. When the cue ball strikes a stationary ball, it transfers momentum to the other ball, causing it to move. If no outside forces (like friction) acted on the balls, their total momentum before and after the collision would remain the same. This illustrates the conservation of momentum well, showing how momentum is transferred between objects but the overall momentum remains constant in the absence of external forces.
Conservation of Energy
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now coming to the energy conservation equation, see, if you look at the energy conservation, you know very well, energy is conserved unless otherwise you have very particular cases. That means, if I have a system like, for example, let us have a pump system here, okay. And it is connected to the inflow, also it is connected to the outflow. That means two pipes we have, connected to that I have a pump.
So, if you look at that, the pump is giving energy to this fluid, okay. We convert from mechanical energy to potential energy. The pump is giving additional energy or work done by the mechanical to the fluid, okay. So, we have exchange of work to this system. Also, as you feel it, if you touch any pumping system, just the outlet level and the inlet pipe, you can see there will be a temperature different. If there is a temperature difference, that means heat transfer is happening.
So, work done is there and also heat transfer is there.
Detailed Explanation
The conservation of energy principle conveys that energy cannot be created or destroyed, only transformed from one form to another. In fluid dynamics, this means that the total energy of a fluid system remains constant unless influenced by external work or heat transfer. For instance, in a pump system, mechanical energy is converted into the potential energy of the fluid. Understanding energy conversion helps engineers design efficient systems. Identifying energy losses, such as friction in pipes or heat loss, is necessary for optimizing performance.
Examples & Analogies
Consider riding a bicycle uphill. You need to exert energy to pedal against gravity. Your muscles do work (mechanical energy), which is transformed into potential energy as you gain height. If you stop pedaling, your bike will eventually slow down and stop. This represents energy conservation; energy is not lost but converted and transferred, similar to how a pump transfers energy to fluid.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Mass Conservation: Mass must remain constant within a closed fluid system.
-
Momentum Conservation: Total momentum remains constant unless subjected to external forces.
-
Energy Conservation: Energy remains constant but transforms between forms during processes.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The mass of water flowing through a pipe remains constant over time, assuming no leaks.
-
When a car accelerates, the increase in its momentum is due to the net external forces applied.
-
A fountain pump converts mechanical energy into kinetic energy as water is ejected upwards.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Mass stays the same, in every game, momentum flows, but forces impose!
📖 Fascinating Stories
-
Imagine a water tank. As you pour water in (mass), it fills up, and when you pour it out, it empties. But no matter the level, the mass stays constant unless you leak—just as silly as a pump that sends energy spinning and whirling without losing energy but transforming it instead!
🧠 Other Memory Gems
-
Remember 'MEP' - Mass, Energy, and Momentum—which are the three key conservation laws.
🎯 Super Acronyms
Think 'MEM' for Mass, Energy, Momentum to recall the basic principles of conservation.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Mass Conservation
Definition:
The principle that mass cannot be created or destroyed in a closed system.
-
Term: Momentum Conservation
Definition:
A principle stating that the total momentum of a closed system is constant unless acted upon by an external force.
-
Term: Energy Conservation
Definition:
A fundamental law stating that energy cannot be created or destroyed but only transformed from one form to another.
-
Term: Reynolds Transport Theorem
Definition:
A fundamental theorem that relates the transport of physical quantities across control volumes within fluid dynamics.