Fluid Dynamics: Reynolds Transport Theorem
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fluid Systems
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will explore the fundamental differences between systems and control volumes in fluid dynamics. Can anyone tell me what they think a 'system' is in the context of fluid mechanics?

I think a system refers to a specific group of fluid particles.

Exactly! A system consists of a defined set of fluid particles or virtual fluid balls. Now, what do we mean by 'control volume'?

Is it the space where fluid can flow in and out?

Precisely! A control volume represents a specified spatial region that allows for the exchange of mass and energy. Remember, systems are about particles, while control volumes focus on spatial dynamics. To help you remember, think of it this way: 'C for Control and C for Space'.

How does this relate to the Reynolds Transport Theorem?

Great question! The Reynolds Transport Theorem helps us relate the behavior of systems to control volumes, establishing the equations governing fluid flows. By understanding these basic concepts, we can tackle complex fluid dynamics problems.
Importance of the Reynolds Transport Theorem
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's dive into the Reynolds Transport Theorem. Why do you think this theorem is vital in fluid mechanics?

It must be crucial for deriving equations used in fluid flow, right?

Correct! The theorem allows us to transfer physical laws from a system framework to a control volume framework. This is key when simplifying problems involving fluid dynamics.

Can you give an example of this in action?

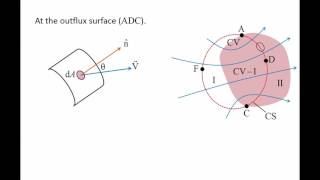
Of course! Consider a nozzle. Using the Reynolds Transport Theorem, we can analyze how fluid enters and exits the nozzle, helping us determine forces acting on it. Remember, 'R for Reynolds, R for Relations'—it's all about establishing relationships!

How do we visualize these flows?

Visualizing flows can be done using virtual fluid balls that represent fluid movement. This will be key as we practice problem-solving in this section.
Challenges in Fluid Mechanics
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

We've previously looked at how fluid dynamics applies in real-world scenarios. Can anyone think of a complex situation in fluid mechanics?

The challenges faced by helicopters navigating through the Himalayas!

Exactly! The unpredictable weather and changing pressure fields are significant challenges that emphasize the need for fluid mechanics. Remember, understanding these conditions requires a solid grasp of our prior concepts.

What specific fluid mechanics principles apply here?

We need to consider buoyancy, pressure changes, and turbulent flow effects. Visualizing these interactions will be pivotal for understanding applied fluid dynamics.

How can we improve our problem-solving skills related to that?

Practicing how to navigate between systems and control volumes while applying the Reynolds Transport Theorem is vital. Remember our mantra: 'Visualize, Relate, Solve!'
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we explore the Reynolds Transport Theorem as a critical tool in fluid dynamics. We discuss the concepts of systems and control volumes, standard challenges in fluid mechanics, and devise methods to approach complex fluid flow problems, enhancing our understanding of fundamental principles and their applications.
Detailed
Fluid Dynamics: Reynolds Transport Theorem
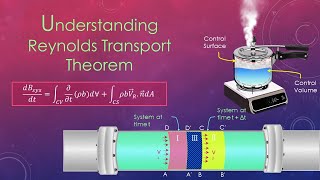
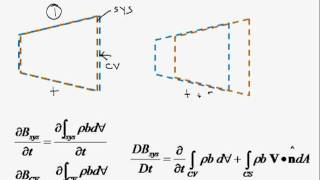
Fluid mechanics is an exciting field that delves into the behavior of fluids, particularly when in motion. This section discusses the essential distinctions between systems and control volumes through the Reynolds Transport Theorem, which allows fluid mechanics problems to be simplified. A system consists of a fixed set of particles, while a control volume is defined by a spatial region through which fluid may flow in and out.
Key Points:
- Control Volume vs System: A system is a fixed group of fluid particles, while a control volume encompasses a defined space where fluid can enter or exit. This distinction is crucial when analyzing fluid behaviors in various contexts.
- Reynolds Transport Theorem: This theorem is fundamental in deriving equations that describe physical phenomena in both systems and control volumes, allowing complex problems to be approached more systematically.
- Real-World Applications: The implementation of these concepts can be seen in real-world scenarios, such as helicopter dynamics in complex terrains where unpredictable weather and flow conditions can yield dangerous situations. Understanding the principles of fluid mechanics through virtual fluid balls allows us to visualize and analyze these scenarios effectively.
Overall, mastering the Reynolds Transport Theorem and its related concepts provides essential tools for addressing real-life fluid dynamics challenges.
Youtube Videos


![Get to know Reynolds Transport Theorem - part I [Fluid Mechanics]](https://img.youtube.com/vi/BwOnHIsgK_Q/mqdefault.jpg)


![Get to know Reynolds Transport Theorem - part II [Fluid Mechanics]](https://img.youtube.com/vi/AGDXYZ2pdTA/mqdefault.jpg)

Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Fluid Dynamics
Chapter 1 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Welcome you to this lecture on fluid mechanics. As we discussed in the last classes, the fluid at rest, which are very simplified cases, we discussed, and today we are going to start very interesting subject on fluid mechanics which is called fluid dynamics. In very simple way we will try to understand the complex fluid flow problems using Reynolds transport theorem and control volume concept.
Detailed Explanation
This section introduces the students to the topic of fluid dynamics, which deals with fluids in motion, as opposed to fluids at rest. The lecturer emphasizes that fluid dynamics will help us understand complex problems in fluid flow by utilizing the Reynolds Transport Theorem and the concept of control volumes, which are areas in space where fluid interactions are analyzed.
Examples & Analogies
Imagine watching a river current. Seeing the way the water flows past rocks and bends makes it clear that fluid dynamics is about understanding how water moves and interacts with its surroundings, just as this lecture will explain using the properties of moving fluids.
Control Volume Concept
Chapter 2 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
I will focus on systems versus control volume concept as well as I will talk about the Reynolds transport theorem, which is a very unique theorem that simplifies very complex problems.
Detailed Explanation
The lecturer plans to discuss two important concepts: 'systems' and 'control volumes.' A system refers to a specific set of fluid particles, while a control volume is a defined space through which fluid flows. The Reynolds Transport Theorem is a mathematical tool that helps relate the laws of fluid mechanics to these two concepts, especially when analyzing fluid flow in a specified control volume.
Examples & Analogies
Think of a garden hose spraying water: the area around the nozzle is your control volume. You can analyze how much water enters and leaves the nozzle, while the specific water molecules over time represent the system. This is how you would apply the concepts in real-life scenarios.
Virtual Fluid Balls Concept
Chapter 3 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
This is a new concept. I brought it for the students to visualize the flow. Once they visualize the flow, then can solve the problems.
Detailed Explanation
The concept of virtual fluid balls (VFB) is introduced as a way to help students better visualize fluid flow. By imagining the fluid as a collection of small balls, students can grasp how these particles move and interact within a control volume, simplifying the complex nature of fluid motion into manageable pieces.
Examples & Analogies
Imagine a crowd of people moving through a doorway. Visualizing them as individual balls helps in understanding how they might cluster, collide, or move around obstacles. This analogy of virtual fluid balls aids in comprehending how fluids flow through different paths and how their behavior can change due to surrounding forces.
Challenges in Fluid Mechanics
Chapter 4 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If you look at the report in Indian Express of January 27, 2018, it says that it has something like twelve major accidents happened to helicopters that took place between almost eight years it in the eastern Himalayas particular to Arunachal Pradesh which lost 55 people.
Detailed Explanation
The lecturer highlights real-world challenges in fluid dynamics, specifically mentioning helicopter accidents in the Eastern Himalayas due to complex weather systems influenced by fluid dynamics. These accidents illustrate how unpredictable changes in airflow and pressure can critically affect the safety and operational stability of aircraft in challenging environments.
Examples & Analogies
Consider flying a kite on a windy day; sudden gusts of wind can cause it to dive or soar unexpectedly. Just like the kite, helicopters must navigate complex wind patterns and changes in air density that can lead to accidents when the pilots cannot anticipate these changes.
Systems vs. Control Volumes
Chapter 5 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, if you can understand this fluid system. When you use the control volume we try to find out not to track individual fluid particles what is happening, but to get it, because of this fluid particle’s movement, what could be the change in pressure distortions...
Detailed Explanation
This section delineates the difference between a system and a control volume. A system consists of a specific set of fluid particles in motion, while a control volume refers to a defined space through which fluids can flow. In analyzing fluids, researchers focus on changes occurring in pressure, velocity, and other properties as fluid enters or exits this defined control volume, rather than tracking each particle individually.
Examples & Analogies
Imagine a large aquarium. Instead of observing every single fish (system), you might observe the filtering system (control volume) that helps maintain water quality. You’re not focused on the individual fish's movements, but rather how effectively the filtration system maintains the health of the environment.
Types of Control Volumes
Chapter 6 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
We have fixed control volume, movable control volume, and deformable control volume. How to define that, that is the problem that we have considered...
Detailed Explanation
The lecturer categorizes control volumes into three types: fixed, movable, and deformable. A fixed control volume remains stationary as fluids flow through it, a movable control volume moves with the fluid (like a ship), and a deformable control volume changes shape or size (like a balloon as air is blown in or released). Understanding these types helps in applying the correct analytical approach to solve fluid dynamics problems.
Examples & Analogies
Consider a bicycle tire. When air is added (deformable), the tire expands; if the tire rolls down a hill (movable), it moves with the bike; however, if we simply observe it while it sits on a stand (fixed), the focus is only on the air inside and the pressure it exerts.
Key Concepts
-
Fluid System: A collection of fluid particles that define a system.
-
Control Volume: A spatial region that allows fluid exchange.
-
Reynolds Transport Theorem: Fundamental theorem for connecting systems to control volumes.
Examples & Applications
A buoyant force acting on a ship floating in water exemplifies principles of fluid dynamics.
The application of the Reynolds Transport Theorem to analyze the pressure changes in a nozzle is a practical use of these concepts.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Fluid flows with grace, in a system or a space.
Stories
Imagine a river flowing with its changing banks; it's like a control volume with fluid moving in ranks.
Memory Tools
R.T. for Reynolds Transport, where system meets the volume—understand and you won’t be a fool 'em.
Acronyms
R.V.S. - Remember Volume and System for understanding Fluid mechanics.
Flash Cards
Glossary
- Fluid System
A defined set of fluid particles functioning together in fluid mechanics.
- Control Volume
A defined spatial region where fluid can enter or exit.
- Reynolds Transport Theorem
A principle that connects the behavior of fluid systems to control volumes, facilitating problem solving in fluid dynamics.
Reference links
Supplementary resources to enhance your learning experience.
