Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Control Volumes
Unlock Audio Lesson
Welcome, everyone! Today, we're diving into control volumes. Can anyone tell me what a control volume is?
Isn't it an area where we analyze fluid flow without worrying about every particle?
Exactly! A control volume allows us to simplify complex fluid flow by focusing on mass, momentum, and energy changes in defined space. We often compare it to focusing on a group of 'virtual fluid balls.' Remember, VFB!
Could you give us an example of a control volume?
Sure! Think of a water pipe. The length of the pipe can be your control volume. We analyze how water flows in and out without tracking each water molecule individually.
And we would want to calculate the forces acting on the flow, right?
Correct! By seeing the inflow and outflow, we can deduce the forces and changes in momentum quite effectively. The crucial part here is that we can apply the principles of conservation.
I see! So it's an efficient way to handle complex situations.
Absolutely! Understanding the control volume concept is essential for effective problem-solving in fluid dynamics.
To summarize, control volumes simplify the analysis by focusing on mass, momentum, and energy exchanges. Just remember how virtual fluid balls represent the fluid within that volume!
Reynolds Transport Theorem
Unlock Audio Lesson
Now that we understand control volumes, let's discuss the Reynolds transport theorem. Does anyone know why this theorem is important?
I think it allows us to relate the particles in a control volume to those in a system?
Exactly! The Reynolds transport theorem gives us a mathematical framework to transition between the system and control volume views. It helps analyze how properties change over time.
What kind of properties are we talking about?
Great question! We're mainly looking at mass, momentum, and energy. By applying the theorem, we can formulate equations that describe the behavior of fluids as they move through defined control volumes.
So, if we have a pump, we can use this theorem to understand energy transfer?
Precisely! The theorem allows us to analyze energy input from the pump against energy losses due to friction or heat. It's vital for designing efficient fluid systems.
To summarize, the Reynolds transport theorem is a bridge between system analysis and control volume analysis, allowing us to derive the fluid properties effectively.
Application of Conservation of Energy
Unlock Audio Lesson
Let's apply what we've learned. Can anyone provide a real-world example of energy conservation in fluid mechanics?
What about water flow through a nozzle?
Excellent example! In this case, we can measure the kinetic energy before and after the nozzle. The reduction in pressure indicates energy conversion.
And this change is the result of energy conservation, right?
Absolutely! Energy conservation dictates that energy cannot disappear; it merely transforms from one type to another. We're analyzing potential energy becoming kinetic energy.
What about movable systems, like ships?
Great point! Ships must deal with drag and lift forces, affecting their movement efficiency. We apply energy conservation to analyze how energy is used to overcome these forces.
In summary, from nozzles to ships, applications of energy conservation help us understand fluid dynamics and improve system efficiency.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section provides a comprehensive overview of the conservation of energy in fluid mechanics, discussing the Reynolds transport theorem, control volumes, and various examples to illustrate how these principles apply in real-world scenarios.
Detailed
Conservation of Energy
In fluid mechanics, the principle of conservation of energy plays a critical role as we analyze the behavior of fluid systems. This section explores how energy is conserved within the frameworks of fluid dynamics, particularly through the lens of the Reynolds transport theorem and control volumes.
Key Concepts
- Control Volumes: Discussing the difference between system and control volume, this section emphasizes how control volumes allow us to study fluid behavior without needing intricate details about individual particles.
- Reynolds Transport Theorem: This theorem bridges the equations at the system level with those at the control volume level, providing a unified approach for analyzing mass, momentum, and energy.
- Applications: Various applications are illustrated, such as the flow through nozzles and movable systems like pumps, highlighting the practical implications of these fundamental principles.
Significance
Understanding the conservation of energy in fluid dynamics not only reinforces theoretical knowledge but also equips engineers and scientists with the tools necessary for addressing complex problems in various fields, including hydraulics and aerodynamics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Conservation Laws in Fluid Mechanics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
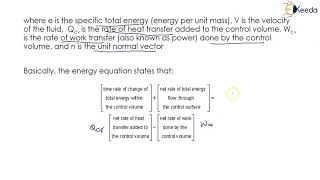
As you know from your twelfth level of knowledge in fluid mechanics as well as solid mechanics, the three basic conservation laws we follow which are mass conservation, momentum conservation which is part of Newton’s second law of motion, then we have the third law which talks about energy conservation, that is the first law of thermodynamics.
Detailed Explanation
In fluid mechanics, three fundamental conservation laws guide our understanding of fluid behavior. Firstly, the conservation of mass states that the mass of fluid in a closed system remains constant over time. Secondly, the momentum conservation principle is aligned with Newton’s laws of motion, which indicates that the momentum of a fluid will remain constant unless acted upon by external forces. Lastly, energy conservation, as outlined in the first law of thermodynamics, maintains that energy cannot be created or destroyed; it can only change forms within the system.
Examples & Analogies
Imagine a water bottle being squeezed. The mass of water inside remains the same (conservation of mass), while the speed of the water coming out changes depending on how hard you squeeze it (momentum conservation). Additionally, the energy you exert by squeezing the bottle transforms into kinetic energy that propels the water out, illustrating energy conservation.
Isolated Systems and Their Characteristics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When we consider a system that means these three conservation principles they are quite valid. When we consider an isolated system like, as I have given examples, the virtual fluid balls, they are isolated systems, okay? They can move at different times. Like, for example, if I consider a system of a set of fluid particles or a set of virtual fluid balls, as you can understand it, there is no change, no other type of mass decaying function is there. The mass will remain constant.
Detailed Explanation
An isolated system means that no matter or energy is exchanged with the surroundings. In such systems, the mass remains unchanged over time, which aligns with the conservation of mass principle. This is vital in fluid mechanics since it helps us predict the behavior of fluids under various conditions without loss or gain of mass throughout the process.
Examples & Analogies
Consider a closed jar filled with air. No air can escape, nor can anything enter the jar. As time passes, the amount of air inside remains constant, illustrating mass conservation in an isolated system.
Changes in Momentum and Forces in a System
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, as you might have solved a lot of physics problems on solid body translations, rotations and all, the basic concept of linear momentum equations you apply, which is, you know, force is rate of change of momentum flux.
Detailed Explanation
When analyzing a fluid system, the changes in momentum are critical for understanding how forces act upon the fluid. The principle states that the net force acting on a system equals the rate of change of momentum within that system. This relationship allows engineers and scientists to predict how fluids will react when forces are applied, whether it's in a pipeline, a tank, or natural water flow.
Examples & Analogies
Think of water coming out of a garden hose. If you block the end of the hose with your thumb (applying a force), the water pressure builds up inside the hose, effectively changing the momentum of the fluid as it accumulates before being released. This demonstrates how an external force alters fluid momentum.
Energy Changes in Fluid Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now coming to the energy conservation equation, see, if you look at the energy conservation, you know very well, energy is conserved unless otherwise you have very particular cases.
Detailed Explanation
Energy conservation in fluid systems indicates that the total energy within that system remains unchanged, barring any losses or gains from external actions. In practical terms, this means if a pump introduces energy to the fluid, this energy must be accounted for in the overall energy equation along with any other forms of energy transfer, like heat.
Examples & Analogies
Consider a kitchen faucet. When you turn it on, the pump increases the water pressure, giving the water potential energy. As the water flows into the sink, that potential energy is converted into kinetic energy—the movement of water. The total energy remains constant as the energy transforms from one form to another.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Control Volumes: Discussing the difference between system and control volume, this section emphasizes how control volumes allow us to study fluid behavior without needing intricate details about individual particles.
-
Reynolds Transport Theorem: This theorem bridges the equations at the system level with those at the control volume level, providing a unified approach for analyzing mass, momentum, and energy.
-
Applications: Various applications are illustrated, such as the flow through nozzles and movable systems like pumps, highlighting the practical implications of these fundamental principles.
-
Significance
-
Understanding the conservation of energy in fluid dynamics not only reinforces theoretical knowledge but also equips engineers and scientists with the tools necessary for addressing complex problems in various fields, including hydraulics and aerodynamics.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Analyzing flow in a water pipe using control volume calculations.
-
Examining the energy loss in a pump system using mass and energy conservation.
-
Fluid acceleration and deceleration through a nozzle, studying energy transformation.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a control volume, flows are bound, mass and energy all around. Through the theorem, we take a glance, at fluid dynamics, let's advance!
📖 Fascinating Stories
-
Imagine a town with flowing rivers. The engineers use control volumes to ensure the water is safe and sound, transforming from one energy to the next, ensuring the town thrives!
🧠 Other Memory Gems
-
C-M-E (Control, Mass, Energy) - Remember these when analyzing fluid systems!
🎯 Super Acronyms
F-M-E (Fluid Mechanics Essentials) - Mass conservation, Momentum conservation, Energy conservation.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Control Volume
Definition:
A defined space through which fluid can flow, allowing for the analysis of mass, momentum, and energy changes.
-
Term: Reynolds Transport Theorem
Definition:
A theorem that relates the change in a property of a fluid system to the change in the same property within a control volume.
-
Term: Mass Conservation
Definition:
The principle stating that mass cannot be created or destroyed in an isolated system.
-
Term: Momentum Conservation
Definition:
The principle that the total momentum of a system remains constant unless acted upon by an external force.
-
Term: Energy Conservation
Definition:
The principle that energy cannot be created or destroyed, only transformed from one form to another.