Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fluid Properties
Unlock Audio Lesson
Welcome to the study of macroscopic analysis in fluid mechanics! Today, we'll explore key fluid properties including density, specific volume, specific gravity, and specific weight. Let's start with density. Can anyone tell me what density is?
Density is mass per unit volume!
Exactly! Density helps us understand how heavy a fluid is. Now, can someone explain how density is calculated?
You divide the mass of the fluid by its volume.
Correct! Remember, density is influenced by the number of molecules in a given volume. Now, let's move on to specific volume.
Isn't that the volume occupied by a unit mass of fluid?
Right! Specific volume is indeed the reciprocal of density. Keep that in mind! Lastly, can anyone define specific gravity for me?
It's the ratio of the density of a substance to the density of a reference substance, right? Usually water?
Exactly! Good job, everyone! These properties are crucial for engineering applications!
Viscosity and Shear Stress
Unlock Audio Lesson
Now let's talk about viscosity. It describes a fluid's resistance to flow. Can anyone describe how viscosity is measured?
Is that the force per area caused by a velocity gradient?
Spot on! Viscosity is associated with shear stress—it becomes higher with an increase in velocity gradient. Anyone aware of what we use to express this relationship?
Newton's laws of viscosity!
Exactly! Under Newtonian fluid conditions, the shear stress is proportional to the velocity gradient. This proportionality constant is called the coefficient of viscosity.
What factors affect viscosity?
Great question! Both temperature and pressure significantly impact viscosity. Colder fluids are generally more viscous. Let's recap the key points discussed!
Continuous vs. Discrete Fluids
Unlock Audio Lesson
Fluid mechanics often assumes fluids behave continuously. Can someone explain what the continuum hypothesis means?
It means we treat fluids as if they are continuous rather than made up of individual molecules?
Correct! This assumption helps simplify calculations and analysis, but at very small scales or high altitudes, this may not hold true. What happens in those cases?
The mean free path becomes significant, and we can't use the continuum hypothesis!
Exactly right! It's important to understand the limitations of this model. Remember, the continuity concept plays a vital role in fluid dynamics and analysis.
Summary and Applications
Unlock Audio Lesson
As we conclude, think about how the properties we've discussed affect various engineering applications. Why is understanding these properties crucial?
It helps us design systems that handle fluids efficiently!
Absolutely! Knowing properties like viscosity and specific gravity can guide our decisions in material selection and system design. Good work today, class!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The macroscopic analysis in fluid mechanics involves understanding fluid properties including density, specific volume, specific gravity, and viscosity. The section discusses the implications of molecular behavior on these properties, the concept of no-slip conditions, and the influence of temperature and pressure on viscosity and surface tension.
Detailed
Macroscopic Analysis
In fluid mechanics, macroscopic analysis is crucial for understanding the behavior of fluids in various conditions. This section covers significant fluid properties, including:
- Density: Defined as mass per unit volume, density is a key factor in determining fluid behavior. It varies based on the volume sampled and is influenced by molecular motion and the correlation of molecules among themselves.
- Specific Volume: This is the volume occupied by a unit mass of fluid, and it is the reciprocal of density.
- Specific Gravity: This property measures the ratio of the density of a substance to the density of a reference substance (usually water), providing insight into whether a fluid is heavier or lighter than water.
- Specific Weight: Denoting the weight (force due to gravity) per unit volume of fluid helps in analyzing fluid flow conditions and applications.
The section also elaborates on Newton's laws of viscosity, exploring both microscopic and macroscopic effects on viscosity, explaining shear stress and its relationship to velocity gradients, and emphasizing the significance of coefficients of viscosity in various fluids. Factors such as temperature and pressure also play an essential role in defining viscosity and surface tension, making an understanding of these properties fundamental in engineering and fluid mechanics studies.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Fluid Behavior
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In fluid mechanics, we analyze fluid behavior both when at rest and in motion, as well as the interaction between fluids and solids at their boundaries. This leads us to fundamental concepts like no-slip conditions.
Detailed Explanation
The behavior of fluids can be observed in two main states: when they are still (at rest) and when they are in motion. A key principle that governs how fluids behave at surfaces is known as the 'no-slip condition.' This means that the layer of fluid in contact with a solid surface does not slip past the surface and moves at the same velocity as the surface itself. This principle is essential in understanding how fluids flow over surfaces.
Examples & Analogies
Imagine a person sliding down a slide covered in water. As they move, the water at the point of contact with their body does not flow past. Instead, it sticks to them, effectively moving at the same speed. This is similar to how fluids behave when they are in contact with solid boundaries.
Flow Classification
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Fluid flows can be categorized into various types such as external flow, internal flow, incompressible flow, and compressible flow.
Detailed Explanation
Fluid mechanics classifies flows based on several criteria. 'External flow' refers to fluid movement around objects (like wind around buildings), while 'internal flow' concerns fluid moving inside a constrained space (like water flowing through a pipe). Additionally, flows are also classified as either incompressible or compressible, which is determined primarily by the behavior of density under pressure changes.
Examples & Analogies
Consider a river (external flow) as water flows around rocks and bends, versus water flowing through a garden hose (internal flow) where it is confined. When you blow up a balloon, the air inside compresses (compressible flow), but under normal conditions, the water in that hose is incompressible, meaning its density remains essentially constant.
Steady vs Unsteady Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In analyzing flows, it's also vital to differentiate between steady flow, where properties like density and velocity do not change over time, and unsteady flow, where these properties fluctuate.
Detailed Explanation
In fluid dynamics, a 'steady flow' means that the fluid's flow properties (like velocity and density) remain constant over time at any given point. In contrast, 'unsteady flow' indicates that these properties can change, possibly due to varying conditions such as temperature or pressure. Recognizing which type of flow you're dealing with is crucial for solving fluid problems.
Examples & Analogies
Think of a water faucet. If you turn it on and leave it at the same level, the water flows steadily; this is steady flow. However, if you frequently turn the faucet on and off or adjust the level, the water flow is unsteady, with varying speeds and pressures.
Microscopic vs Macroscopic Uncertainty
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Microscopic uncertainty occurs when sampling volumes are extremely small, leading to significant variations in density. Conversely, macroscopic uncertainty arises from very large sampling volumes, which may not reflect the true average properties of the fluid.
Detailed Explanation
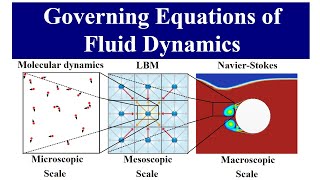
Microscopic uncertainty affects measurements taken in very tiny volumes of fluid where random molecular motion causes variations that don't represent the fluid's bulk properties. On the other hand, macroscopic uncertainty comes into play when sampling volumes are so large that they include uneven distributions within the fluid, leading to an inaccurate representation of density or other properties. Understanding the scale of measurement is important to minimize these uncertainties.
Examples & Analogies
Imagine trying to measure the density of water by taking a drop from a glass. Because you're only looking at that tiny drop, it might not reflect the entire glass's average density due to the water's random molecules. Now, think about filling a swimming pool. Its density is more stable, but if you sample just a corner of it, the varying depths might mislead you about the overall density. These examples show that the scale impacts how well we can understand fluid characteristics.
Defining Continuum Hypothesis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The fluid is typically treated as a continuous medium, allowing us to use concepts like continuous and differentiable functions of density, pressure, and velocity.
Detailed Explanation
In fluid mechanics, we often treat fluids as continuous substances, which allows us to apply calculus to describe their behavior. This means we can express properties such as density and pressure as functions of space and time, treating them as smooth variations instead of discrete jumps between individual molecules. This assumption simplifies many analyses and helps create equations that describe fluid flow effectively.
Examples & Analogies
Think of a rope being waved up and down. Although the rope is made of many individual fibers, you can describe its motion as a smooth wave. In the same way, fluids are treated as continuous, letting us easily analyze their movement instead of focusing on every single molecule.
Limitations of the Continuum Hypothesis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
While using the continuum hypothesis is commonly applicable, it becomes invalid at very high altitudes or in microfluidic applications where molecular behavior cannot be overlooked.
Detailed Explanation
The continuum hypothesis assumes that fluids can be analyzed as if they were continuous, which works well at most scales. However, this breaks down in conditions such as extremely high altitudes, where the mean free path between molecules increases, making them behave more like individual particles than a bulk fluid. Similarly, in microfluidic systems, the effects of individual molecules become significant and cannot be ignored in modeling fluid behavior.
Examples & Analogies
At high altitudes, like in helicopters or planes, there are so few air molecules that they behave differently than at sea level. This is akin to trying to swim in a pool but being in a starting block instead of the water; you can feel the individual water molecules. In microfluidic applications, similar effects can be felt in tiny channels where the interactions at the molecular level change how liquids behave, much like how a river flows differently than a small stream.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Macroscopic Analysis: Understanding fluid behavior through properties like density and viscosity.
-
Density: A critical property defined as mass per unit volume.
-
Specific Volume: The volume occupied by a unit mass of fluid.
-
Specific Gravity: Ratio of the density of a substance to water's density, indicating heaviness.
-
Viscosity: Resistance of a fluid to flow, expressed through shear stress and velocity gradients.
-
Continuum Hypothesis: An assumption that fluids behave continuously for simpler analyses.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Water has a density of approximately 1000 kg/m³ at standard conditions.
-
Oil has a specific gravity less than 1, indicating it is lighter than water.
-
In a pipe flow scenario, understanding viscosity helps in calculating pressure losses.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Density’s dense, it’s mass over space,
🧠 Other Memory Gems
-
let's embrace!
📖 Fascinating Stories
-
Imagine a river flowing smoothly; the thickness of the water determines how easily boats can navigate—this is viscosity in action!
🧠 Other Memory Gems
-
Remember the acronym D-S-G-V: Density, Specific Volume, Gravity, Viscosity to recall key fluid properties.
🎯 Super Acronyms
Use **DVS** to remember Density, Viscosity, and Specific Gravity directly relates to liquid behavior!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Density
Definition:
Mass per unit volume of a substance, usually expressed in kg/m³.
-
Term: Specific Volume
Definition:
The volume occupied by a unit mass of fluid, the reciprocal of density.
-
Term: Specific Gravity
Definition:
The ratio of the density of a substance to the density of a reference substance (usually water).
-
Term: Specific Weight
Definition:
Weight per unit volume of a substance, typically expressed in N/m³.
-
Term: Viscosity
Definition:
A measure of a fluid's resistance to flow or deformation.
-
Term: Shear Stress
Definition:
The force per unit area exerted parallel to the surface.
-
Term: Newton's Law of Viscosity
Definition:
The principle stating that shear stress is proportional to the rate of strain (velocity gradient).
-
Term: Continuum Hypothesis
Definition:
An assumption in fluid mechanics that a fluid is continuous and does not consist of discrete molecules.