Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Viscosity
Unlock Audio Lesson
Today, we will explore viscosity, a key property of fluids. Viscosity measures a fluid's resistance to flow. Can anyone tell me what factors might affect this resistance?
I think temperature might affect how thick or thin a fluid is.
Great observation! Temperature indeed influences viscosity. Normally, as temperature increases, viscosity decreases for liquids. What else?
I guess the type of fluid also matters, right? Like honey is more viscous than water.
Exactly! We often categorize fluids based on their viscosity, leading us to talk about Newtonian and non-Newtonian fluids. Let’s remember: thicker fluids tend to have higher viscosity.
Newton's Laws of Viscosity
Unlock Audio Lesson
Now, let’s delve into Newton's laws of viscosity. Can anyone summarize what they understand about shear stress and shear rate?
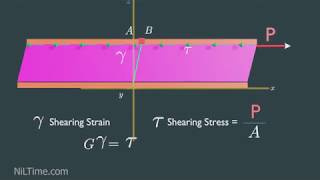
Isn’t shear stress the force per unit area acting parallel to the fluid layers?
Exactly! For Newtonian fluids, shear stress is directly proportional to the velocity gradient. If we denote shear stress by τ and the velocity gradient by du/dy, we can express this with the equation τ = μ (du/dy), where μ is the dynamic viscosity.
So, if I have a greater velocity difference between layers, does that mean I have a greater shear stress?
Correct! The greater the velocity gradient, the greater the shear stress, provided the viscosity remains constant.
Applications and Implications of Viscosity
Unlock Audio Lesson
Let’s consider applications of viscosity in real-world scenarios. Why do you think viscosity is important in engineering?
It probably affects how fluids flow in pipes or around surfaces.
Absolutely! In engineering, understanding viscosity is crucial for designing systems involving fluid transport, such as pipelines or hydraulic systems. What else might we consider?
Maybe how temperature control is needed in mechanical systems to ensure efficient fluid flow?
Yes! Temperature control is vital since viscosity changes with temperature. Efficient operations require managing these variations.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section delves into the concept of viscosity as a physical property of fluids, explaining both microscopic and macroscopic views, its behavior under varying conditions, and Newton's laws. It illustrates how viscosity relates to the flow characteristics of fluids, highlighting its importance in engineering and real-world applications.
Detailed
Detailed Summary of Viscosity
Viscosity is a key property of fluids that measures their resistance to shear or flow. This section explores viscosity from both microscopic and macroscopic perspectives, discussing how it affects fluid motion and interactions. The chapter begins by recapping fluid behavior, emphasizing the importance of no-slip conditions, and expands on fundamental fluid properties such as density, specific volume, specific gravity, and specific weight.
Newton's laws of viscosities are the focus here, where the relationship between shear stress and shear rate is highlighted. Shear stress is shown to be directly proportional to the velocity gradient between fluid layers, with the proportionality constant being the coefficient of viscosity. Additionally, the effects of temperature and pressure on viscosity are reviewed, illustrating both theoretical and practical implications in various fluid flow applications. The conclusion underscores the significance of understanding viscosity in engineering scenarios, such as flow through pipes and interactions within different fluid dynamics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Viscosity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us go to the very interesting concept, the Newton's laws of viscosities, okay, which is very simplified, simple common laws of viscosity which we use for solving many of the problems in laminar and also approximate for other flow conditions.
Detailed Explanation
This section introduces viscosity as a fundamental concept in fluid mechanics related to the flow of fluids. Viscosity demonstrates how fluids respond when they are subjected to deformation or flow, reflecting the internal friction among their molecules. Newton's laws of viscosity act as guidelines for understanding fluid behavior in various scenarios, such as laminar or turbulent flow.
Examples & Analogies
Imagine trying to push a heavy object across a surface. The resistance you feel is similar to viscosity in fluids; it represents the internal resistance flowing molecules have against each other. Just as harder surfaces require more force to move objects over them, fluids with higher viscosity require more force to flow.
Understanding No-Slip Condition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As we know it that whenever we have the fluid flow conditions, we will have the no-slip conditions. That means, at these locations I will have the velocity zero. At these locations the contact of the fluid particles on the solid surface will give a velocity equal to the velocity of the plate.
Detailed Explanation
The no-slip condition is a fundamental assumption in fluid mechanics that states fluid at a solid boundary moves at the same velocity as the boundary itself. This means that when a fluid flows over a surface, the layer of fluid molecules directly in contact with that surface does not slip – they have zero velocity at the boundary. This condition is critical for accurately modeling fluid flow and predicting how fluids will behave when in contact with solid surfaces.
Examples & Analogies
Consider a slow-moving river where the water at the edges is almost stationary because it sticks to the riverbank. The water flowing faster in the center lets you visualize the no-slip condition; the water at the edges is not slipping past the riverbank, just as fluid molecules do not slip past a solid boundary.
Flow Layers and Shear Stress
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look it that you have the plate, okay. If you can look it which is at the rest conditions and you have in the top another plate is there, where you are applying a force F and the velocity V is it is moving this plate.
Detailed Explanation
This segment discusses how the application of force creates layers of fluid flow. When one plate moves while the other is still, the fluid layer in contact with the moving plate experiences a velocity, causing adjacent layers of fluid to move as well. The interaction between these layers generates shear stress, a measure of how much force is applied over a specific area between these layers, affecting how the fluid flows.
Examples & Analogies
Think of it as layers of frosting on a cake; if you apply a light pressure on the top layer, it begins to slide over the layers beneath it, creating friction between each frosting layer. This friction is akin to the shear stress in fluid mechanics, showcasing how different layers of fluid interact through applied force.
Viscosity and Shear Stress Relationship
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
After certain time maybe these two velocity is coming to equilibrium. That means they will be the same order, same value. So looking these the mass exchange and the momentum exchange of the molecules at this the artificial interfaces between two packets of the fluid packets.
Detailed Explanation
When the two fluid packets (layers) eventually reach the same velocity, they establish a consistent flow pattern. The relationship between shear stress and velocity gradient is described by Newton's law of viscosity, where the shear stress is directly proportional to the rate of change of velocity between layers. The viscosity serves as the proportionality constant, varying between different fluids based on molecular structure and interaction.
Examples & Analogies
Imagine stirring honey with a spoon; the slower the movement of the spoon, the thicker and more resistant the honey feels due to its viscosity. In contrast, water flows easily without much resistance. This difference showcases how varying viscosities result in differing responses to applied forces.
Coefficient of Viscosity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
And that proportionality is known as the coefficient of viscosity or dynamic of viscosity.
Detailed Explanation
The coefficient of viscosity is a measure of a fluid's internal resistance to flow, reflecting its viscosity. It quantifies how shear stress relates to the velocity gradient, providing valuable insights into how different fluids behave under similar conditions. This coefficient varies depending on the fluid type due to molecular properties.
Examples & Analogies
If you have a collection of liquids, like water, oil, and syrup, pouring them will result in different flow rates. This variance represents their coefficients of viscosity; the thicker the fluid, like syrup, the higher its viscosity and the slower it flows compared to water.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Viscosity: A measure of a fluid's resistance to flow.
-
Shear Stress: Force exerted by fluid layers parallel to each other.
-
Shear Rate: The rate at which adjacent layers of fluid move with respect to each other.
-
Newtonian Fluids: Fluids with constant viscosity irrespective of shear rates.
-
Dynamic Viscosity (μ): A property of fluids that quantifies their internal resistance to flow.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of honey versus water illustrates significantly different viscosities: honey is more resistant to flow.
-
The design of pipelines for oil transport considers viscosity and temperature to ensure efficient flow.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Viscosity’s the fluid’s glue, makes it flow slow, not too fast or too true.
📖 Fascinating Stories
-
Imagine a race between water and honey, where honey moves slowly, taking its time, while water speeds by with ease.
🧠 Other Memory Gems
-
The acronym WISH (Water is Slippery Honey) can help remember the relation: Viscosity makes fluids flow 'not too fast'.
🎯 Super Acronyms
SPEED (Shear Stress, Proportional, Every Degree) can help recall Newton’s law of viscosity.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Viscosity
Definition:
The measure of a fluid's resistance to flow or deformation.
-
Term: Shear Stress
Definition:
The force per unit area acting parallel to the fluid layers.
-
Term: Shear Rate
Definition:
The rate of change of velocity at which one layer of fluid moves relative to another.
-
Term: Newtonian Fluid
Definition:
A fluid whose viscosity remains constant regardless of the shear rate.
-
Term: Dynamic Viscosity
Definition:
A measure of a fluid's internal resistance to flow; often denoted by the symbol μ.