7.3.1 - Lagrangian and Eulerian Frames
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fluid Motion Description
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we begin our exploration of fluid kinematics, focusing on two fundamental approaches: the Lagrangian and Eulerian frames. Can anyone tell me how these frames fundamentally differ?

Is it related to whether we track individual particles or measure things at fixed locations?

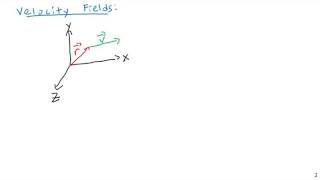
Exactly! The Lagrangian frame focuses on tracking fluids using individual particles, while Eulerian measures properties at fixed points. Remember: **L** for **L**ocation = **E**ulerian.

So, if I were to observe how concentrations change in water pollution, I'd use the Eulerian approach at different points?

That's correct! By using probes at fixed points, you can create a concentration map over time.

And what about Lagrangian? Would I just follow a single particle?

Yes! You would observe how that particle's path changes with velocity over time.

It sounds like both methods are important in applications!

Absolutely! Understanding both helps in real-world fluid dynamics problems.
Practical Application of the Lagrangian Approach
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s discuss the Lagrangian approach further. Who can give me an example of where this approach might be applicable?

Could it be used in tracking pollutants from a source in a river?

Exactly! As you track a pollutant particle, you observe how velocity and concentration change. And these tracked particles are often referred to as *virtual fluid balls*.

So if I'm analyzing a virtual fluid ball, what key properties should I measure?

Great question! You would want to measure velocity, pressure, and any changes in concentration as it flows. Remember, **VPC**: Velocity, Pressure, and Concentration!

This helps in understanding complex flow patterns too, right?

Absolutely! It helps to visualize flow patterns and understand dynamic fluid behaviors.
Understanding the Eulerian Framework
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let’s shift our focus to the Eulerian framework. What would you say this approach values in its measurements?

It values fixed locations and measures how properties vary at those places.

Correct! You might place probes at different locations to gather how velocity or pressure changes over time. It’s about being stationary! Remember, **E** for **E**xamination - measuring at points.

If water flows past a stationary probe, how will that probe’s readings change?

The readings will reflect the changes in flow fields as different fluid particles pass over the probe over time.

What about practical applications? Where is this useful?

It's hugely beneficial in environmental analysis, like monitoring pollutant concentrations at water treatment plants.

Seems like both approaches complement each other.

Exactly! They provide a comprehensive picture for analyzing fluid behavior.
The Importance of Virtual Fluid Balls
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Finally, let’s touch on virtual fluid balls. How do they fit into the Lagrangian and Eulerian perspectives?

Are they a bridge between the two methods?

Absolutely! They help visualize the transition between tracking particles and examining fixed points.

Can you use them to better predict flow behavior in CFD?

Yes! Using virtual fluid balls can aid in understanding complex simulations and interpreting CFD results effectively.

That makes sense and seems really useful!

It is! And as a memory aid, remember **VFB**: Virtual Fluid Ball, connecting Lagrangian and Eulerian concepts.

Thanks for all these insights!

You're welcome! Always remember, combining both perspectives deepens your understanding of fluid mechanics.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section explores the Lagrangian and Eulerian frameworks in fluid mechanics, contrasting their approaches to analyzing fluid flow and emphasizing the significance of each method. It offers practical examples using concepts like virtual fluid balls, streamlines, and the measurements of concentration.
Detailed
Detailed Summary
The section covers two critical frames of reference in fluid mechanics: Lagrangian and Eulerian.
Lagrangian Framework
In the Lagrangian perspective, fluid motion is described by tracking individual fluid particles or a collection of virtual fluid balls. This method emphasizes the particle's path and allows for observing variations in velocity, pressure, and concentration as fluid particles move through time and space.
Eulerian Framework
The Eulerian approach, on the other hand, involves measuring fluid properties at specific fixed points in space over time. This method focuses on analyzing how velocity, pressure, and concentration change at specific locations, regardless of the fluid particles passing those points.
Virtual Fluid Balls
The text introduces the concept of virtual fluid balls as a metaphorical tool that bridges the Lagrangian and Eulerian descriptions, facilitating understanding of fluid flow patterns and behaviors.
The application of both frameworks is critical in applications such as analyzing pollution dispersion in bodies of water or understanding vortex shedding in aerodynamic contexts.
In summary, grasping both Lagrangian and Eulerian systems not only complements theoretical knowledge in fluid kinematics but also enhances practical applications when dealing with real-world fluid dynamics complexities.
Youtube Videos

![Lagrangian Description and Eulerian Description [Fluid Mechanics]](https://img.youtube.com/vi/27m1I-DlOik/mqdefault.jpg)






Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Lagrangian and Eulerian Descriptions
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
When we describe fluid flow, we typically use two frameworks: Lagrangian and Eulerian. The Lagrangian perspective tracks individual fluid particles as they move through space and time, while the Eulerian perspective focuses on specific locations in the flow field and measures the properties of the fluid at those locations.
Detailed Explanation
The Lagrangian frame of reference follows each fluid particle's journey, documenting its position and properties as it travels through the fluid. On the other hand, the Eulerian perspective takes a fixed viewpoint, measuring the fluid's characteristics (like velocity or pressure) at specific points in space, regardless of which particles are currently passing through those points. This fundamental difference shapes how each method analyzes fluid dynamics.
Examples & Analogies
Imagine you are at a parade (Lagrangian perspective), watching the individual floats and how each one moves along the route. Alternatively, consider you are standing at a specific intersection (Eulerian perspective), measuring how many floats pass by in a given time. Each method gives you different insights into the parade dynamics!
Understanding Eulerian Frames
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In the Eulerian frame, measurements are taken at fixed points. For example, if a person uses a probe to measure the concentration of pollutants in water released downstream from an industry, the changing concentration can be represented as a function of time at that fixed location.
Detailed Explanation
The Eulerian approach collects data at fixed positions, letting us understand how the fluid's properties (like velocity, pressure, and concentration) change over time at those locations. This method is especially useful in analyzing flow fields over time and can create maps of concentration changes as the fluid moves.
Examples & Analogies
Think about a weather station that gathers data on temperature and wind speed at a specific location. The information it collects helps forecasters understand local weather patterns, just as an Eulerian frame helps us understand fluid properties at specific points.
Exploring Lagrangian Frames
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Conversely, in the Lagrangian frame, we follow a specific fluid particle (or virtual fluid ball) through the flow and see how its properties change as it moves through the fluid field. If the particle experiences pollution, we can record how its concentration varies as it travels.
Detailed Explanation
In this approach, the focus is on the individual fluid particles and their paths. When tracking these particles, we examine their velocity, pressure, and other characteristics as they move through the fluid, allowing us to observe real-time changes in their properties.
Examples & Analogies
Imagine yourself on a ride in an amusement park that follows a specific path (Lagrangian perspective). As you travel along, you notice how the view changes. If instead, you were fixed at a point in the park (Eulerian perspective), you'll see every ride as it passes by without experiencing the ride yourself.
Combining Both Perspectives
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Both Lagrangian and Eulerian perspectives are valuable for fluid mechanics. They provide different insights that can be used together to analyze and solve complex fluid flow problems. For example, understanding particle movements alongside fixed measurements allows for a more comprehensive view of the flow phenomena.
Detailed Explanation
Using both approaches allows engineers and scientists to analyze fluid flow from multiple angles. For instance, CFD (Computational Fluid Dynamics) simulations can incorporate both perspectives to predict how pollutants disperse in water bodies, combining data about movement (from the Lagrangian approach) with fixed readings (from the Eulerian approach).
Examples & Analogies
It's like a detective solving a case by interviewing witnesses (Lagrangian) while also reviewing surveillance footage from a fixed camera (Eulerian). The complete picture is obtained by combining personal accounts with a broader view.
Virtual Fluid Balls Concept
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The concept of virtual fluid balls serves as a bridge between Lagrangian and Eulerian frames. It provides a way to visualize fluid study by tracking particles while simultaneously being able to understand the field properties, thus offering an intermediate perspective.
Detailed Explanation
Virtual fluid balls allow us to think of fluid motion in terms of both individual particles and their cumulative behavior in a flow field. This hybrid approach helps simplify complex calculations and visualizations, making it easier to model fluid dynamics in practical applications like environmental engineering or hydrodynamics.
Examples & Analogies
Consider a busy city where individual cars (virtual fluid balls) move through traffic but are also part of a larger flow pattern on the roads (Eulerian field). By observing both the traffic of individual cars and the overall flow at intersections, we can better manage and understand city traffic dynamics.
Key Concepts
-
Lagrangian Frame: Focuses on individual particle paths in fluid flow.
-
Eulerian Frame: Focuses on properties of fluids as they pass fixed points.
-
Virtual Fluid Balls: A conceptual tool that aids in understanding fluid dynamics by bridging the two frames.
-
Streamlines: Lines that illustrate flow paths in steady fluid motion.
Examples & Applications
Tracking a pollutant in a river using the Lagrangian method by observing a single particle's path.
Analyzing the concentration of wastewater at a sewage treatment plant using the Eulerian method with fixed probes.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In Lagrange, we track the flow, in Euler we just watch it grow.
Stories
Imagine a boat on a river (Lagrangian) versus a person on a bank observing the current (Eulerian). The boat tells the story; the person records the tale.
Memory Tools
Remember LE: Lagrangian for Location tracking; Eulerian for Examination of fixed points.
Acronyms
Use **VFB** for Virtual Fluid Balls, bridging the two approaches.
Flash Cards
Glossary
- Lagrangian Frame
A perspective that tracks individual fluid particles over time to observe changes in properties.
- Eulerian Frame
A perspective that focuses on measuring fluid properties at fixed points within the flow.
- Virtual Fluid Balls
An intermediate concept used to bridge Lagrangian and Eulerian perspectives, aiding visualization of fluid flow.
- Streamlines
Imaginary lines that represent the paths followed by fluid particles in a steady flow.
- Concentration
The amount of a substance in a given volume of fluid, often measured in environmental analysis.
Reference links
Supplementary resources to enhance your learning experience.
