Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Flow Regimes
Unlock Audio Lesson
Today, we're diving into the different flow regimes in open channel flow—subcritical, critical, and supercritical flows. Who can tell me about the Froude number?
Isn’t the Froude number a ratio between the inertia forces to the gravitational forces in the flow?
Exactly! The Froude number helps us classify flow based on its behavior. Can anyone tell me what it indicates when the Froude number is less than 1?
That means we are in a subcritical flow regime, where gravity forces dominate, right?
That's correct! And what can you say about disturbances in subcritical flow?
Disturbances can propagate both upstream and downstream.
Great! So how about when the Froude number is greater than 1?
That's supercritical flow, where inertia forces dominate, and disturbances only propagate downstream.
Excellent! Remember this sequence: less than 1 is subcritical, equal to 1 is critical, and greater than 1 is supercritical—let’s use the acronym 'S-C-S' to remember 'Subcritical-Critical-Supercritical'.
Today, we covered that in subcritical flow, gravity is the boss, while in supercritical flow, inertia takes charge. Always remember the Froude number helps us identify these flow types!
Hydraulic Jumps
Unlock Audio Lesson
Let’s talk about hydraulic jumps. Who can explain what a hydraulic jump is?
Isn’t it a sudden transition from supercritical to subcritical flow, causing turbulence?
Absolutely! What happens to the energy during a hydraulic jump?
There’s a lot of energy loss because of the turbulence created.
Exactly! And why might hydraulic jumps be useful in canal design?
They help with aeration and can control energy dissipation in water flow.
Right! They also promote mixing, which can be beneficial for certain chemical processes. A mnemonic to remember their benefits is 'AMIX': Aeration, Mixing, Inertia control, and eXplosion (of energy loss).
Today, we learned that hydraulic jumps not only control flow transitions but also serve vital functions like aeration and energy dissipation. Remember 'AMIX' for their applications!
Energy Loss in Open Channels
Unlock Audio Lesson
We’ve covered hydraulic jumps; now let’s discuss energy loss in open channels. Why is energy consideration vital in designing canal systems?
Energy loss affects the efficiency of the flow, right?
Exactly! Energy must be conserved. If we have two sections in a canal, how can we represent energy loss mathematically?
We can use Bernoulli's equation and calculate the specific energy at both points!
Correct! And what does the specific energy represent in context?
It's the total energy per unit weight of fluid, combining pressure head, velocity head, and elevation head.
Great summary! Understanding specific energy helps to design efficient open channels. A good phrase to remember could be 'EPV', which stands for Energy, Pressure, and Velocity. These are your energy heads!
Today, we established the importance of energy conservation in open channels, along with calculating specific energy and its implications. Remember 'EPV' to keep track of energy heads!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section delves into the significance of hydraulic jumps in open channel flow, exploring the dynamics of energy loss during flow transitions from supercritical to subcritical regimes. It introduces key principles such as the Froude number and energy conservation equations that enhance understanding of flow behavior in natural and man-made channels.
Detailed
Hydraulic Jumps and Energy Loss
Hydraulic jumps are crucial phenomena in open channel flow characterized by significant energy dissipation and flow regime changes. The relationship between flow velocity, flow depth, and the speed of surface waves is pivotal, as it determines the flow regime—subcritical, critical, or supercritical—defined by the Froude number. The section explains:
- Flow Regimes:
- Subcritical Flow (Froude number < 1): Here, gravitational forces dominate. Disturbance waves propagate upstream and downstream, influencing upstream conditions.
- Critical Flow (Froude number = 1): In this unique state, the gravity and inertia forces equate, leading to no disturbance propagation.
- Supercritical Flow (Froude number > 1): Inertia forces dominate, and disturbances do not propagate upstream.
- Hydraulic Jumps: These occur when flow transitions from supercritical to subcritical regimes, leading to turbulent mixing and energy loss. They have practical applications in canal designs to optimize aeration and energy dissipation.
- Energy Loss in Open Channels: Energy loss is a key consideration in designing hydraulic systems, particularly in stabilizing flows and ensuring efficient energy usage. The relationship between specific energy and flow depth is graphically represented to help visualize energy changes during different flow regimes.
Youtube Videos
![Open Channel Flow 38 - {How to calculate sequent depth and energy loss in hydraulic jump problem]](https://img.youtube.com/vi/eAjApbk4NhA/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Hydraulic Jumps
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Turbulence formations you can see just downstream of dam structures you can see the turbulence because of the formations of hydraulic jump. This is what called its hydraulic jump and we try to design a hydraulic jump because at these hydraulic jumps the mixing process and the aeration process happen very dominantly no doubt there is energy losses that happen, which is required for some of the cases. But the hydraulic jumps which are created from the supercritical flow to subcritical flow at the transition zones make a sound noise and create turbulent structures because of that you can have significant energy losses. These jumps are necessary for the formation of mixing and the erosion processes.
Detailed Explanation
Hydraulic jumps occur when a flow transitions from a supercritical state (fast, low depth) to a subcritical state (slow, high depth). In this transition, the flow can experience turbulence and create waves on the surface. Although hydraulic jumps lead to energy loss in the flow, they serve important functions like mixing water, introducing air (aeration), and supporting certain erosive processes that can be necessary for river engineering and ecology.
Examples & Analogies
Imagine a river flowing quickly over a steep drop (like a small waterfall). As the water rushes down, it hits a calm pool below where the water is deeper. This sudden change creates waves and bubbles—this is similar to a hydraulic jump, which helps to mix the water and introduce oxygen into it, much like how frothing milk introduces air into coffee.
Understanding Flow Characteristics and Energy Loss
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you commit that the speed of the surface wave as I take it very simple way that let here have a flat channels okay and I have the depth of the flow is there and I just make a piston here. Okay. So there is a piston here and this piston is moving it let be del V and this is the fluid at rest having let be y depth and this is what the surface wave having a depth of delta y and it is moving with velocity C0.
Detailed Explanation
When we consider flow in a flat channel, we can visualize the flow with the help of a simple analogy. If we think of a piston moving in a liquid, it creates a surface wave due to its displacement. This analogy helps in understanding how surface waves propagate with speed, denoted as C0. This speed is crucial for understanding wave behavior in open channel flows, especially when it comes to analyzing energy losses at hydraulic jumps.
Examples & Analogies
Think of a child pushing a toy boat across a still pond. As the child pushes, waves ripple outward from the boat, similar to how a piston creates waves. These ripples can change depending on how hard the child pushes, akin to how water waves behave in engineering applications. Each ripple might make the water more turbulent, similar to how hydraulic jumps create turbulence in rivers.
Froude Number and Flow Classification
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If the Froude number is less than 1, that means the gravity force is more than the inertia forces we define this case as subcritical flow. When you have very rare occurrences, it occurs when the inertia force is equal to the gravity forces of the flow system; that is called critical flow. If the Froude number is greater than 1, we call it supercritical flow.
Detailed Explanation
The Froude number is a dimensionless number that helps classify the type of flow in an open channel. In subcritical flow (Froude number < 1), gravity forces dominate, and surface waves can travel upstream. Critical flow (Froude number = 1) is a unique state where the flow conditions are balanced. In supercritical flow (Froude number > 1), inertia forces dominate, and disturbances cannot propagate upstream—only downstream. This classification is crucial for designing hydraulic structures.
Examples & Analogies
Imagine a skateboarder on a ramp. If they go down the ramp slowly (subcritical), they can easily adjust and maneuver back up if needed. However, at a high speed (supercritical), the skateboarder cannot go back up the ramp; they must move forward. Similarly, the Froude number helps engineers understand whether water behavior in a channel is manageable or if it is moving too quickly to control.
Energy Loss in Open Channel Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
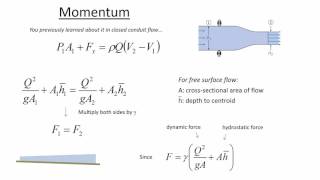
When we construct a canal, the flow of water can become very flat which means the slopes are very slight. Typically, the energy stoic graphs ensure that we can solve for two sections, as seen in the energy loss equations, where the energy at one section equals the energy at another section plus the energy loss.
Detailed Explanation
In open channel flows, especially in flat channels like canals, we can analyze energy loss between sections of the flow. By applying principles similar to Bernoulli's equation, we can relate the energy levels at different points of the canal. The difference in energy is considered energy loss due to factors like turbulence and changes in channel shape. Understanding these losses helps engineers design effective water management systems.
Examples & Analogies
Think of it like a water slide at a theme park. As you slide down, some energy is lost to friction and turbulence in the water, which slows you down slightly by the time you reach the pool at the bottom. This 'energy loss' is similar to what happens in canals where engineers must account for these losses to ensure that the desired flow rate is achieved.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydraulic Jump: A transition that causes turbulence and energy loss.
-
Froude Number: A key parameter that helps classify flow regimes.
-
Energy Loss: A critical factor in the efficiency of open channel designs.
-
Subcritical Flow: Characterized by gravity forces dominating.
-
Supercritical Flow: Characterized by inertia forces dominating.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A hydraulic jump in a canal downstream of a dam can visibly show energy dissipation through turbulence.
-
The effective design of canals in India, such as the Ganga Canal, utilizes concepts of hydraulic jumps to ensure efficient water distribution.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When Froude's less than one, gravity's your king, flows down like a bun, a super jump it will bring.
📖 Fascinating Stories
-
Imagine a river encountering a sudden drop; it quickly transitions from fast to slow, transforming into a swirling pool—this is how hydraulic jumps work, energizing the water.
🧠 Other Memory Gems
-
Remember 'GIC' for the gravity, inertia, and change in flow that hydraulic jumps create.
🎯 Super Acronyms
Use 'SCS' to recall the flow types
- Subcritical - Critical - Supercritical.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydraulic Jump
Definition:
A sudden transition from supercritical to subcritical flow, resulting in turbulence and energy loss.
-
Term: Froude Number
Definition:
A dimensionless number used to classify flow regimes based on inertia and gravity forces.
-
Term: Energy Loss
Definition:
The dissipation of energy due to turbulence and friction in fluid flow, crucial for efficient hydraulic designs.
-
Term: Subcritical Flow
Definition:
Flow regime characterized by a Froude number less than 1, where gravity forces dominate.
-
Term: Supercritical Flow
Definition:
Flow regime characterized by a Froude number greater than 1, where inertia forces dominate.