Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding 1D Consolidation Assumptions
Unlock Audio Lesson
Today, we will discuss the assumptions of Terzaghi’s 1D Consolidation Equation. Can anyone name one of the assumptions?
One assumption is that the soil medium is completely saturated.
Exactly! Now, why is it important for the soil to be saturated?
Because if the soil isn't saturated, the pore water pressure theories wouldn’t hold!
Good point! Another assumption is that the soil is isotropic and homogeneous. What does that mean?
It means that the properties of the soil are the same in all directions, right?
Yes, correct! This uniformity simplifies our calculations. Remember, acronyms like 'SH' for 'Saturated' and 'Homogeneous' can help you recall these assumptions!
What are some limitations of this 1D theory?
Great question! Limitations include the assumption of constant permeability and the simplification of flow to one dimension. These aspects may not hold true in real-world scenarios.
In summary, the solid assumptions of saturation, isotropy, and homogeneity allow us to utilize Terzaghi's equation, while being mindful of its limitations in application.
Impact of Stress on Consolidation
Unlock Audio Lesson
Now let’s delve into the role of vertical stress during consolidation. What happens to pore water when we apply stress?
The pore water is expelled, leading to soil consolidation.
Exactly! The change in volume is equal to the volume of water expelled due to the stress. How can this be quantified?
I think it's related to the degree of consolidation, which is measured as 'u', right?
Yes! The degree of consolidation, `u`, indicates how much consolidation has taken place at a particular point in the soil. It’s important to note how this might vary with depth.
Why does `u` vary with depth? Isn’t it the same for the entire soil layer?
Good question! The degree of consolidation varies because the excess pore water pressure isn't evenly distributed across the depth. Placement of loads can lead to different levels of consolidation depending on the depth.
To summarize, the relationship between vertical stress and pore water pressure is fundamental to understanding soil behavior under load.
Finding Average Degree of Consolidation
Unlock Audio Lesson
Let’s discuss how we calculate the average degree of consolidation over an entire depth. Who can explain why this average is crucial?
Because it gives us an overall understanding of how the soil will behave under consistent loading.
Exactly! This average provides key insights for engineers. How do we define and calculate it?
Is it just an average of the `u` values across depths?
Yes, that’s correct! We take the `u` values at various depths and average them out to get an overall consolidation.
Are there any special considerations we need to keep in mind while doing this?
Indeed. The non-dimensional terms are used to express the relationship of these variables effectively and to ensure accuracy in the calculation.
Remember, understanding the average degree of consolidation is crucial for predicting long-term settlement of foundations.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section elaborates on the assumptions underlying Terzaghi's 1D consolidation theory, the implications of these assumptions, and the limitations faced in realistic scenarios. Key concepts include the average degree of consolidation, which varies with depth and time in soil layers under stress, and how the understanding of excess pore water pressure is framed within this context.
Detailed
Detailed Summary
This section centers around Terzaghi's 1D Consolidation Equation, which is pivotal for understanding the behavior of saturated soils under load. The assumptions made for this equation are crucial to its applicability: the soil must be saturated, isotropic, and homogeneous; Darcy's law applies; and water flow is one-dimensional. The consolidation hypothesis posits that changes in soil volume are directly related to the volume of pore water expelled due to changes in vertical stress. Notably, the section highlights that, as consolidation progresses, variables such as permeability (Kz) and the coefficient of volume compressibility (mv) are no longer constant, challenging the assumptions of standard 1D consolidation models. Limitations include simplifying the flow to one dimension and assuming uniform excess pore water pressure distribution during loading. The average degree of consolidation, noted as u, varies spatially and temporally, and is critical for geotechnical engineering applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Importance of Average Degree of Consolidation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
From practical point of view, the average degree of consolidation over the entire depth at any given time is desirable.
At any given time u varies with location and hence the degree of consolidation also varies.
Detailed Explanation
The average degree of consolidation is a crucial aspect when studying how saturated soils react under loading. It helps in understanding the overall behavior of the soil over its entire depth, not just at a single point. The degree of consolidation (u) reflects how much the soil has settled or compressed at any particular depth due to external loading. It varies depending on the location within the soil layer, indicating that not all parts of the soil consolidate equally when exposed to the same stresses.
Examples & Analogies
Consider a sponge soaked in water. When you press down on the sponge, different areas might release water at different rates based on their structure. Similarly, in a soil layer, when weight is applied (like a building), some parts will compress and release water more quickly than others. The average degree of consolidation helps us understand the behavior of the entire sponge of soil under pressure.
Defining Average Degree of Consolidation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The average degree of consolidation for the whole soil deposit at any time is given by...
Detailed Explanation
The average degree of consolidation is calculated by considering the degree of consolidation (u) at various depths and averaging these values. This gives engineers and geologists a clearer picture of the soil's behavior over time, especially when assessing how much the soil has settled due to loading. It’s important for predicting future behavior and ensuring any structures built on it will be stable and safe.
Examples & Analogies
Imagine you are measuring how much a pile of dough has flattened when you press it down. If you take measurements from various spots on the dough, some areas might have flattened more than others. By averaging these measurements, you can get an overall idea of how much the entire pile has changed shape. This average helps you understand the dough's response to pressure, similar to how the average degree of consolidation helps understand soil behavior.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Degree of consolidation (u): Represents the extent of consolidation achieved over time and depth.
-
Coefficient of permeability (Kz): The measure of how easily water can flow through the soil.
-
Assumptions of consolidation theory: Essential parameters assumed for applying Terzaghi’s equation effectively.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: If a soil layer experiences a vertical load causing an increase in stress, the degree of consolidation can be monitored over time to better assess future foundation stability.
-
Example 2: By applying Terzaghi’s equation, engineers can predict the changes in pore water pressure and subsequent settlements for various loading conditions.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Saturated soil, pressure on hold, under stress it shrinks, as the water sinks.
📖 Fascinating Stories
-
Once in a land of soil deep, Terzaghi's magic helped the farmers to keep, their fields from sinking with loads so high, as water flowed out, the soil waved goodbye.
🧠 Other Memory Gems
-
Remember SH for Saturated and Homogeneous in 1D consolidation.
🎯 Super Acronyms
COVeR for Coefficient of Volume compressibility, One-dimensional flow, Vertical stress, and Reduction in pore water pressure.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Onedimensional consolidation
Definition:
A simplification in soil mechanics where consolidation is considered to occur primarily in one vertical dimension.
-
Term: Coefficient of permeability (Kz)
Definition:
A property of soil that denotes the ability of water to flow through it.
-
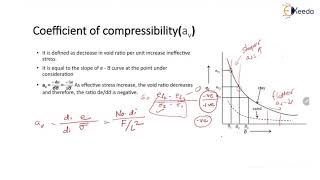
Term: Coefficient of volume compressibility (mv)
Definition:
A measure of how much a given volume of soil compresses under an applied load.
-
Term: Excess pore water pressure
Definition:
The pressure within the soil pores that exceeds the atmospheric pressure.
-
Term: Degree of consolidation (u)
Definition:
A dimensionless ratio that expresses the fraction of consolidation achieved at a specific depth and time.