Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to 1D Consolidation
Unlock Audio Lesson
Today, we'll explore Terzaghi's 1D Consolidation Equation. Can anyone explain what consolidation means in terms of soil mechanics?
I think it's about how soil shrinks or compacts under loads.
Exactly! It refers to the reduction in volume of a saturated soil due to applied loads. Now, let's talk about the assumptions this equation makes. What are some key assumptions?
The soil is completely saturated.
And it has to be isotropic, right?
Great points! We also assume that water flow follows Darcy’s law, and hear this: if we remember the acronym S.I.C.H. for Saturation, Isotropic, Constant permeability, and Homogeneous, we can easily recall these crucial characteristics. Let's delve deeper.
Key Hypotheses of Consolidation
Unlock Audio Lesson
Let's shift gears to the key hypotheses behind 1D consolidation. Who can tell me the relationship between volume change and pore water?
The volume change in soil equals the volume of pore water that is expelled!
That's right! This relationship is essential to understand. As soil compresses, the expelled pore water leads to a reduction in voids. What about the height change?
The height change is also directly related since the compression occurs vertically.
Spot on! Remember, this vertical alignment is a significant aspect of Terzaghi's equation. It helps in visualizing the consolidation process effectively.
Limitations of the 1D Consolidation Equation
Unlock Audio Lesson
Now, let’s tackle the limitations of this equation. Can anyone explain why assuming constant permeability can be problematic?
Because as the soil consolidates, the voids become smaller, which changes the permeability!
Exactly! As consolidation progresses, both permeability and volume compressibility can change, leading to inaccurate predictions. What are some other limitations?
It assumes the flow is always one dimensional, but in reality, it could be three-dimensional.
Correct! It's crucial for engineers to understand these limitations to apply the theory effectively. Remember, context matters!
Solar Consolidation Concepts
Unlock Audio Lesson
Let’s discuss drainage conditions during consolidation. What's the difference between single and double drainage?
Single drainage has one drainage path at the top or bottom, while double drainage allows flow from both sides.
Excellent! This can significantly affect the rate of consolidation and the distribution of excess pore water pressure. Anyone aware of how these conditions might impact construction projects?
Well, faster drainage can mean quicker construction times, right?
Correct! That’s important for project planning. Understanding drainage conditions is vital in your future designs.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Terzaghi's 1D consolidation equation outlines the necessary conditions and assumptions for accurate analysis of soil consolidation. It explores the primary factors impacting consolidation, while also addressing the limitations of the equation, particularly concerning changes in permeability and dimensionality of flow.
Detailed
Detailed Summary of Terzaghi’s 1D Consolidation Equation
Terzaghi's 1D Consolidation Equation is fundamental in understanding the behavior of saturated soils under load. This section outlines the conditions under which the equation holds, including:
- Assumptions: It assumes that the soil is isotropic, homogeneous, completely saturated, and that water flow follows Darcy’s law in a one-dimensional vertical pattern. Other assumptions include constant permeability, constant volume compressibility, and incompressibility of soil particles and water.
- Key Hypotheses: The foundational hypothesis includes that the change in soil volume equals the volume of expelled pore water, relating directly to changes in void ratio and soil height during compression.
- Limitations: Key limitations discussed include the assumption of constant permeability and volume compressibility, which may not hold over time as consolidation progresses, leading to variability in excess pore water pressure development within a stratum. The section also outlines how potential boundary conditions, such as drainage methods, impact pore water pressure distribution and consolidation time.
Understanding Terzaghi’s equation is crucial for engineers working with compressible soils, as it provides a framework for predicting settlement and consolidation behavior under loading conditions.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Assumptions of 1D Consolidation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
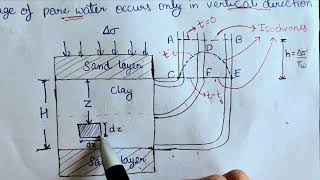
The following assumptions are made for the soil medium during the consolidation process:
- The soil medium is completely saturated
- The soil medium is isotropic and homogeneous
- Darcy’s law is valid for flow of water
- Flow is one-dimensional in the vertical direction
- The coefficient of permeability is constant
- The coefficient of volume compressibility is constant
- The increase in stress on the compressible soil deposit is constant
- Soil particles and water are incompressible
Detailed Explanation
These assumptions establish the foundation for Terzaghi's one-dimensional consolidation theory. Key points include that the soil is fully saturated, meaning all voids are filled with water. Isotropic and homogeneous indicate that the properties of the soil are uniform in all directions. Darcy's law is crucial, as it governs how water flows through the soil. Assuming one-dimensional flow simplifies our analysis to vertical movement only. The constants mentioned (coefficient of permeability and volume compressibility) imply that these characteristics do not change as the soil consolidates, which is a simplification but necessary for initial calculations. Finally, it is assumed that soil and water do not compress, which treats them as incompressible materials.
Examples & Analogies
Think of the soil as a sponge soaked with water. Just like a sponge has a uniform texture and structure, we imagine the soil is similar. The assumptions help us predict how the sponge will behave when we start squeezing it - we expect water to be expelled steadily without any changes in the sponge's material properties.
Volume Change in Soil
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
One-dimensional theory is based on the following hypotheses:
- The change in volume of soil is equal to volume of pore water expelled.
- The volume of pore water expelled is equal to change in volume of voids.
- Since compression is in one direction, the change in volume is equal to change in height.
Detailed Explanation
This chunk elaborates on how the consolidation process can be analyzed. The first hypothesis emphasizes that when the soil compresses, the water that was in the pores of the soil is pushed out, leading to a decrease in volume. The second hypothesis clarifies that this expelled water is directly related to the volume of the spaces (voids) in the soil that fill with water. The last point highlights that since this process occurs in one direction (vertically), the overall effect is a change in height of the soil column.
Examples & Analogies
Imagine a balloon filled with water. When you apply pressure, water goes out of the balloon's opening, similar to how pore water is expelled during soil consolidation. The more you press, the less water is retained, just like the soil loses volume as it consolidates.
Stress Changes in Consolidation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The increase in vertical stress at any depth is equal to the decrease in excess pore water pressure at that depth.
Detailed Explanation
This principle states that when external loads are applied on the soil, there is an increase in vertical stress. This stress acts to expel excess pore water pressure within the soil. Essentially, as more weight is added above the soil, the pressure from the weight forces water out of the soil's pores, leading to consolidation. This relationship helps us understand how stress and pore pressure interact during consolidation.
Examples & Analogies
Think of a sponge lying under a heavy book. When the book is placed on the sponge, it compresses the sponge and pushes out some of the water trapped inside. The heavier the book, the more water is expelled, showing how vertical stress can cause changes in pore water pressure.
Limitations of 1D Consolidation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Limitations of 1D consolidation include:
1. In the deviation of the 1D equation, the permeability (Kz) and coefficient of volume compressibility (mv) are assumed constant, but as consolidation progresses, void spaces decrease, resulting in decreased permeability.
2. The flow is assumed to be 1D, but in reality, flow can be three-dimensional.
3. The application of external load is assumed to produce excess pore water pressure over the entire soil stratum, but sometimes it does not develop uniformly.
Detailed Explanation
The limitations highlight some flaws in the assumptions used in Terzaghi’s model. First, as soil consolidates, its voids shrink, causing permeability to change, which goes against the assumption of it being constant. Secondly, while we idealize flow as one-dimensional, actual flow can spread out and be more complex. Lastly, when weight is applied, the resulting pore pressure does not always distribute evenly throughout the soil; varying conditions can lead to localized changes that the simple model does not account for.
Examples & Analogies
Consider a sponge again, but with varying thicknesses at different spots. If you apply pressure on one end, the water may not flow uniformly throughout it. Some spots may retain more water due to how tight or loose the sponge is, showing that real-world conditions are often more complex than simplified models suggest.
Degrees of Consolidation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
From a practical point of view, the average degree of consolidation over the entire depth at any given time is desirable. At any given time, u varies with location, and hence the degree of consolidation also varies.
Detailed Explanation
In practice, engineers and geologists often want to know the average degree of consolidation (denoted as 'u') throughout the entire depth of the soil. This is because, at any single moment, different locations within the soil may have varied degrees of consolidation due to the differences in stress and pore water pressure at those points. Understanding this average helps manage and design safe structures on or within the soil.
Examples & Analogies
If you consider a layer cake where each layer is made up of different textures, even if you apply frosting on the top, the way the frosting settles will vary depending on how dense each layer is. Similarly, different areas of soil may consolidate differently, requiring us to assess the average behavior to understand how the entire cake (or soil) will hold up under weight.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Saturated Soil: Soil that is fully soaked with water, leading to different mechanical behaviors under load.
-
Darcy’s Law: A principle that describes the flow of fluid through porous media.
-
Coefficient of Volume Compressibility: Indicates the change in volume per unit increase in pressure.
-
Excess Pore Water Pressure: Pressure exerted by pore water above the hydrostatic pressure.
-
Vertical Stress: The stress acting vertically on a soil layer due to applied loads.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When a load is applied to clay soil, the excess pore water pressure temporarily increases until drainage occurs, leading to consolidation.
-
In a construction project on soft ground, understanding the consolidation process helps predict settlement and plan for foundation design.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When soils squish and water's near, consolidation's what we must revere.
📖 Fascinating Stories
-
Imagine a sponge being pressed; as water escapes, it becomes compressed. This mirrors how soils react under load.
🧠 Other Memory Gems
-
Remember 'HAS CoPiSm' for conditions: Homogeneous, Anisotropic, Saturated - Coefficient of Permeability, Incompressible, Soil.
🎯 Super Acronyms
Use 'SIC' for Saturated, Isotropic, Constant to remember key characteristics of soil in 1D consolidation.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Consolidation
Definition:
The process by which a saturated soil decreases in volume as it expels pore water under pressure.
-
Term: Incompressible
Definition:
A characteristic of materials that do not change in volume under pressure.
-
Term: Homogeneous
Definition:
Having a uniform composition throughout.
-
Term: Isotropic
Definition:
Properties are the same in all directions.
-
Term: Coefficient of Permeability
Definition:
A measure of the ease with which water can move through soil.
-
Term: Degree of Consolidation
Definition:
The ratio of change in voids to total change in voids during consolidation.