Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Pore Water Pressure
Unlock Audio Lesson
Today we are going to discuss uniform excess pore water pressure with depth. Can anyone remind me what pore water pressure means?
Isn’t it the pressure exerted by water in the soil pores?
Exactly! Pore water pressure plays a crucial role in soil behavior, especially under load. Now, can someone explain what 'uniform excess pore water pressure' refers to?
I think it’s the additional pressure in the pore water due to external loads, but it's constant at different depths?
Correct! This idea is fundamental to Terzaghi’s one-dimensional consolidation theory.
Assumptions of One-Dimensional Consolidation
Unlock Audio Lesson
Now let's look into the assumptions of the one-dimensional consolidation theory. What is the first assumption?
The soil is fully saturated, right?
Yes! Full saturation is critical. What else do we assume about the soil?
It has to be isotropic and homogeneous. That means properties are the same in all directions.
Great! Remember, these assumptions help simplify calculations, but they also have limitations.
Limitations of One-Dimensional Consolidation
Unlock Audio Lesson
Let’s talk about the limitations. Can someone summarize one major limitation?
Well, as consolidation continues, the permeability of the soil changes.
Exactly! The coefficient of volume compressibility also changes with applied stress. How does this affect our calculations?
It means our results may not be accurate if we assume they are constant.
Right! Always question the validity of the assumptions in practical scenarios.
Draining Scenarios
Unlock Audio Lesson
Let’s apply our understanding to drainage scenarios. What do we mean by single drainage?
That would be drainage at the top and bottom being impervious.
Perfect! And how about double drainage?
That’s when both the top and bottom can drain, right?
Excellent! These scenarios impact how fast excess pore water pressure dissipates with time.
Degree of Consolidation
Unlock Audio Lesson
Now let’s move to the degree of consolidation. Why is this significant?
It helps us understand how much of the consolidation process has occurred.
Yes! Over time, the degree of consolidation varies, and that impacts how we manage soil structures. Can someone summarize today’s key points?
We covered pore water pressure, the assumptions of our consolidation theory, its limitations, drainage conditions, and its importance.
Great summary! Remember these concepts as they are fundamental to geotechnical engineering.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section delves into the characteristics of uniform excess pore water pressure with depth in saturated soils, detailing the assumptions underlying Terzaghi's consolidation equations. It also highlights limitations of the theory, such as variations in permeability and the nature of drainage.
Detailed
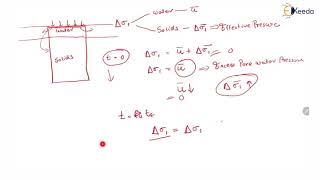
Uniform Excess Pore Water Pressure with Depth
The section discusses the concept of uniform excess pore water pressure in soil layers subjected to stress. It starts with a set of assumptions that underpin the one-dimensional consolidation theory:
- The soil is completely saturated, isotropic, and homogeneous.
- Darcy’s law applies to water flow, which is considered one-dimensional.
- Permeability and volume compressibility coefficients are constant.
- Stress increases uniformly across the compressible soil deposit.
- Soil particles and water are incompressible.
These assumptions lead to the understanding that changes in the soil's volume are directly related to the volume of pore water expelled, which in turn affects the excess pore water pressure. The section highlights significant limitations, such as the assumption of constant permeability and compressibility, which is unrealistic in varying physical conditions. Finally, the discussion introduces the principles of single and double drainage scenarios and emphasizes that excess pore water pressure and consolidation degree can vary with time and depth, affecting the overall soil behavior during the consolidation process.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Single Drainage
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Single Drainage (Drainage at top and bottom impervious)
Detailed Explanation
Single drainage refers to a situation where water can only escape from one side of the soil layer. In this case, one side is impervious, meaning it does not allow water to pass through. Only the open side can drain excess pore water, affecting how the soil consolidates over time. This drainage condition slows down the rate at which pore water pressure dissipates.
Examples & Analogies
Imagine a sponge that's only allowed to release water from one side while the other side is sealed. The water can escape from the open side, but the sealed side holds onto it, which affects how quickly the sponge can compress. This is similar to how single drainage operates in soil consolidation.
Double Drainage
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Double Drainage (Drainage at top and bottom)
Detailed Explanation
Double drainage occurs when water can escape from both the top and bottom of the soil layer, making it easier for excess pore water to dissipate. This drainage condition usually leads to a quicker rate of consolidation compared to single drainage since the pressure can equalize from both sides, resulting in more uniform changes in pore water pressure throughout the soil column.
Examples & Analogies
Think of a two-sided sponge. If you apply pressure and allow water to escape from both sides, the sponge will compress more quickly compared to if it was only letting water out from one side. This faster drainage leads to quicker consolidation of the soil.
Variables in Excess Pore Water Pressure
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- The depth z 2. The excess pore water pressure _u 3. The time (t) after application of loading
Detailed Explanation
Three key variables influence excess pore water pressure: depth (z), excess pore water pressure itself (_u), and time (t) after applying a load to the soil. Depth affects the hydrostatic pressure on pore water, excess pore water pressure indicates the soil's tendency to compress, and time represents how long the load has been applied, which influences how long it takes for consolidation to occur.
Examples & Analogies
Imagine a heavy book placed on a sponge. The depth of the sponge (how thick it is), the amount of water that gets pushed out (pore water pressure), and how long the book stays on the sponge all affect how much the sponge will compress and regain its shape once the weight is removed.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
One-Dimensional Consolidation: A theoretical approach to model how soil consolidates under applied vertical load.
-
Uniform Excess Pore Water Pressure: The concept that excess pore water pressure remains constant with depth in certain scenarios.
-
Coefficient of Volume Compressibility: A key property indicating how much volume soil changes under stress.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a single drainage scenario, if water is not escaping through the bottom layer, the consolidation rate will be slower compared to a double drainage setup.
-
When applying a load on saturated clay, the initial excess pore water pressure will increase until consolidation reduces it as water is expelled.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When pore pressure feels a load, consolidation's in active mode.
📖 Fascinating Stories
-
Imagine a sponge soaked with water under a heavy book. As you apply weight, the water starts to seep out, showing how excess pore water pressure changes.
🧠 Other Memory Gems
-
When recalling the assumptions of consolidation, remember 'I S.P.V.S.C' - Isotropic, Saturated, Permeability constant, Volume compressibility consistent.
🎯 Super Acronyms
DRAIN for drainage conditions
- Double or Single
- Resistance
- Allows water
- Impervious
- Natural conditions.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Pore Water Pressure
Definition:
The pressure of water within the soil pores.
-
Term: Consolidation
Definition:
The process by which soil changes volume in response to applied pressure.
-
Term: Single Drainage
Definition:
A condition where drainage is only permitted at one surface of the soil layer.
-
Term: Double Drainage
Definition:
A condition where drainage is allowed at both the top and bottom of the soil layer.
-
Term: Coefficient of Volume Compressibility
Definition:
A measure of the soil's change in volume in response to applied pressure.