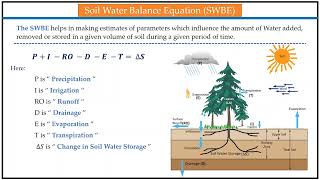
Water Balance Equation
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Water Balance Equation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we are going to discuss the Water Balance Equation, which is crucial in hydrology. This equation helps us understand how water is conserved within a system. It's formulated as P equals ET plus Q plus change in storage. Does anyone know what P stands for?

I think P stands for Precipitation!

Yeah, and that means it's the total amount of water coming into the system, right?

Exactly! Precipitation is a key input. Now, what do you think ET stands for?

Is it Evapotranspiration? It’s the sum of evaporation and the water lost from plants.

Great job! Yes, ET represents both evaporation from surfaces and transpiration by plants. So far, we have P for precipitation and ET for evapotranspiration. What about Q?

That's the runoff, right? The water flowing away from the system?

Correct again! And lastly, what does ΔS represent?

It stands for change in storage, which shows how much water is held in systems like soil or aquifers?

Exactly! So the complete equation represents the balance of all these water components—understanding this helps when analyzing the water resources of any system.

To summarize, the Water Balance Equation is P = ET + Q + ΔS where each component helps us see how water flows through our environment.
Application of the Water Balance Equation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we know the components of the Water Balance Equation, let's talk about its applications. Can anyone think of where this might be useful?

Maybe in watershed management?

Yes! It's essential for watershed studies as it allows us to understand water storage and flow. What else?

How about in agriculture? Farmers need to know how much water to use for irrigation!

Exactly! Agricultural water budgeting involves calculating how much water is available and needed. Who can tell me why reservoir operation might require this equation?

It helps in managing the inflow and outflow effectively to ensure enough water supply.

Great answer! Understanding water inputs and outputs is vital for efficient reservoir management. Let's do a quick recap of how this equation applies in different scenarios: watershed studies to analyze flow patterns, in agriculture to ensure proper irrigation, and for reservoirs to manage water levels.
Understanding Terms in the Equation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

To delve deeper into the relationship among these components, let's analyze how one affects the other. If there is a heavy rainfall, what happens to each component?

Well, if P increases, then ET might increase too, but maybe there’s more runoff as well.

Right! And if there's increased Q, then change in storage would probably decrease unless ET also increases.

Perfect! You all are grasping how these variables interact. It’s important to understand these dynamics when managing water resources. Now, just to test your knowledge: What happens if we have a drought?

Then P would be low, and ET would still happen, it could lead to negative changes in storage!

Exactly! In a drought scenario, insufficient precipitation input can lead to decreased storage and thereby affect plant health and water supplies.

Let’s summarize: the Water Balance Equation helps us understand how precipitation, evapotranspiration, runoff, and storage changes interrelate and affect one another.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section introduces the Water Balance Equation, delineating its components: precipitation, evapotranspiration, runoff, and change in storage. Understanding these variables is crucial for various hydrological applications, including watershed studies and agricultural water budgeting.
Detailed
Water Balance Equation
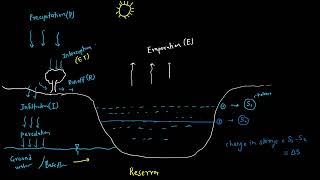
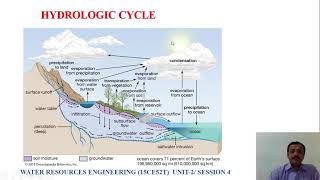
The Water Balance Equation is a fundamental concept in hydrology, aligned with the law of conservation of mass, which states that water in a system must be accounted for through its inputs, outputs, and changes in storage. The equation is expressed as:
P = ET + Q + ∆S
Where:
- P = Precipitation: The total amount of water received in a given time frame.
- ET = Evapotranspiration: The sum of evaporation and transpiration from the land and water surfaces.
- Q = Runoff: The water that flows over the land surface and through the subsurface, contributing to rivers and streams.
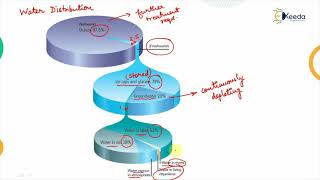
- ∆S = Change in Storage: Represents the variation in water stored in the soil moisture, groundwater, or surface water over time.
The application of the Water Balance Equation is extensive, serving critical roles in watershed studies, reservoir operation management, and agricultural water budgeting. Such analyses facilitate effective planning and management of water resources, making it imperative for engineers and hydrologists to grasp its implications thoroughly.
Youtube Videos





Audio Book
Dive deep into the subject with an immersive audiobook experience.
Concept of the Water Balance Equation
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The water balance equation is based on the law of conservation of mass. It relates the input, output, and storage of water in a system.
Detailed Explanation
The water balance equation is a fundamental concept in hydrology that illustrates the conservation of water within a defined system. It states that the amount of water entering a system (input) must equal the amount of water leaving the system (output) plus any changes in the storage of water within that system. This principle helps us understand the dynamics of water in natural and engineered environments.
Examples & Analogies
Think of the water balance equation like a bathtub. When you fill the bathtub with water (input), the water level rises. If you drain some water (output) or if the water seeps away (change in storage), the water level drops. To maintain the water level, the amount of water flowing in has to match the amount flowing out plus what is lost, just like how we look at water in the hydrologic system.
Components of the Water Balance Equation
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
P = ET + Q + ∆S
Detailed Explanation
In the equation, 'P' represents precipitation, which is the water input to the system. 'ET' stands for evapotranspiration, which includes both evaporation from surfaces and transpiration from plants, representing the water output. 'Q' denotes runoff, which is the water that flows over the land and returns to water bodies, also contributing to output. Finally, '∆S' indicates the change in storage, which can be soil moisture, groundwater, or surface water. Understanding these components is essential for accurately analyzing water resources.
Examples & Analogies
Imagine a sponge (representing the land and water sources). Rainwater collects in it (precipitation, P), some water evaporates or is used by plants (evapotranspiration, ET), some water runs off the sponge onto the floor (runoff, Q), and the amount of water trapped in the sponge can increase or decrease (change in storage, ∆S). The balance between these factors determines how much water remains in the sponge.
Applications of the Water Balance Equation
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The water balance equation has various applications including watershed studies, reservoir operation, and agricultural water budgeting.
Detailed Explanation
The water balance equation is a powerful tool used in multiple areas of water resource management. In watershed studies, it helps assess how much precipitation is available for different uses and how much can be expected to runoff into streams and rivers. For reservoir operation, it allows for managing water levels effectively, ensuring that enough water is available for downstream needs while also maintaining storage for future use. Additionally, in agricultural water budgeting, it assists farmers in understanding how much water they have for irrigation purposes, enabling better planning and resource use.
Examples & Analogies
Consider a farmer planning irrigation for a crop. By applying the water balance equation, the farmer can analyze how much rain is expected (P), how much water will be lost through evaporation and transpiration (ET), and how much water might runoff or remain in the soil for plant use (Q and ∆S). This helps the farmer effectively manage water resources to ensure healthy crops and sustainable farming practices.
Key Concepts
-
Water Balance Equation: Equation representing the relationship of input, output, and storage of water.
-
Conservation of Mass: The principle that mass in a closed system must remain constant.
-
Hydrology Applications: Various fields that utilize the Water Balance Equation for effective water resource management.
Examples & Applications
In a reservoir, if precipitation is 200 mm and evaporation plus transpiration is 100 mm, and runoff is 50 mm, then the change in storage can be calculated as: ΔS = 200 - (100 + 50) = 50 mm.
During a drought, if precipitation drops to 30 mm while evapotranspiration remains at 60 mm and runoff at 15 mm, the change in storage would be: ΔS = 30 - (60 + 15) = -45 mm, indicating water depletion.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Pee, eee, cue, and delta, these are the water terms we remember!
Stories
Imagine a thirsty plant in the forest. It drinks rainwater (P), sweats out water (ET), the creek carries away surplus (Q), and changes in the soil moisture (ΔS) tell us if the plant is thriving or wilting.
Memory Tools
To recall the Water Balance Equation: 'Pediatrics Elevate Quiet Ducks' - where P is Precipitation, E is Evapotranspiration, Q is Runoff, and ΔS is change in Storage.
Acronyms
PETQ for P=Precipitation, E=Evapotranspiration, T=Water Transfer, Q=Runoff, ΔS=Change in Storage.
Flash Cards
Glossary
- Precipitation
The total amount of water, in any form, that falls to the Earth.
- Evapotranspiration
The sum of evaporation and transpiration from the land and water surfaces.
- Runoff
Water that flows over the land surface and through the subsurface, contributing to rivers and streams.
- Change in Storage (ΔS)
The variation in water stored in soil moisture, groundwater, or surface water over time.
Reference links
Supplementary resources to enhance your learning experience.
