Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.

Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.

Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Scalars
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Let's start by discussing scalar quantities. Scalars are defined solely by their magnitude. Can anyone give me an example of a scalar?

Mass! Like 70 kg.

Correct! Mass is a perfect example of a scalar. What about another one?

Time is also a scalar, right? Like 30 seconds.

Exactly! Time is a scalar because it tells us how long something occurs but not the direction it takes. Remember, scalars have no direction. Let's summarize scalars as quantities like mass, time, temperature, distance, and energy.
Introduction to Vectors
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Now let's move on to vector quantities, which are really important in physics! Can someone tell me what makes a vector different from a scalar?

Vectors have both magnitude and direction!

Exactly! For instance, if I say a car is traveling at 60 km/h to the east, that's a vector because it specifies both speed and direction. Who can give me another example of a vector?

Displacement! Like saying I walked 5 km north.

Perfect! Displacement tells us how far we are from the starting point and in what direction. When representing vectors, remember arrows: the length shows the magnitude, and the way the arrow points indicates the direction.
Comparing Scalars and Vectors
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Let’s compare scalars and vectors now. What are some key differences between these two types of quantities?

Scalars only need a number, while vectors need both a number and direction.

Correct! For example, 80 km/h is just speed, a scalar; but 80 km/h east is velocity, a vector. Scalars include mass and energy, while vectors cover displacement and force. Can someone summarize this for us?

Scalars have magnitude only, while vectors have both magnitude and direction. Scalars can't tell us 'which way,' but vectors can!

Excellent summary! Understanding this difference is crucial for solving physics problems related to motion and forces.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
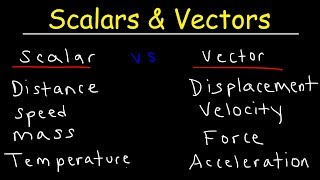
Scalars are quantities defined solely by their magnitude, such as mass and temperature, while vectors require both magnitude and direction, like displacement and velocity. Understanding the distinction between these types of quantities is crucial for problem-solving in physics.
Detailed
In physics, physical quantities are classified into two main categories: scalars and vectors. Scalar quantities are those that can be described entirely by their magnitude (or size) without reference to direction, such as mass, temperature, and energy. For example, if an object has a mass of 70 kg, the number '70 kg' alone defines the quantity without needing a direction.
Conversely, vector quantities require both a magnitude and a direction for their full description. Examples of vector quantities include displacement, velocity, force, and momentum. For instance, stating that an object has a displacement of 5 kilometers to the north provides a comprehensive understanding of its position and path taken. Vectors are often represented graphically via arrows, where the arrow's length indicates magnitude, and its direction shows the quantity's orientation. This distinction is vital for correct analysis and application in various physical scenarios, especially when dealing with motion and forces.
Youtube Videos


Audio Book
Dive deep into the subject with an immersive audiobook experience.
Scalar Quantities
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Physical quantities in physics can be broadly classified into two categories based on whether they possess direction.
Scalar Quantities: These are quantities that are completely described by their magnitude (size or amount) alone. They do not have any associated direction.
Examples:
- Mass: A person's mass is 70 kg. The '70 kg' fully describes the quantity; it doesn't have a direction.
- Time: It takes 20 seconds to run a distance. '20 seconds' is sufficient.
- Temperature: The room temperature is 22 °C.
- Distance: You walked 5 kilometers. This describes the total path length, regardless of turns.
- Speed: A car travels at 80 km/h. This tells you how fast, but not which way.
- Energy: A battery stores 100 Joules of energy.
- Volume: A bottle holds 1.5 liters of liquid.
Detailed Explanation
Scalar quantities are measurements that only have magnitude, meaning they represent how much of something there is without any reference to direction. For instance, when you say a mass is 70 kg, it clearly tells you the size of the mass but doesn't include any direction in which the mass is structured. Similarly, time, temperature, distance, speed, energy, and volume are also scalar quantities because they provide values that do not require directional context for their full understanding. This makes scalars straightforward and easier to quantify in various contexts.
Examples & Analogies
Think of a recipe. If a recipe says you need 200 grams of flour, it tells you exactly how much flour is needed, but it doesn't matter where you place that flour on the kitchen counter. It is purely how much, not about where it goes, similar to how scalar quantities operate.
Vector Quantities
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Vector Quantities: These are quantities that require both magnitude (size) and direction for their complete description. The direction is crucial for understanding the effect of the quantity.
Examples:
- Displacement: You walked 5 kilometers North. This tells you both how far you are from your starting point and in what direction.
- Velocity: A car travels at 80 km/h East. This specifies both speed and direction.
- Force: You push a box with a force of 50 Newtons to the right. The direction of the push determines its effect.
- Acceleration: An object is accelerating at 9.8 m/s² downwards (due to gravity).
- Momentum: A measure of the mass and velocity of an object, indicating its 'quantity of motion' in a specific direction.
Detailed Explanation
Vector quantities differ from scalar quantities because they not only include a numerical value (magnitude) but also the direction associated with that value. For instance, if you say you walked 5 kilometers North, it means you are not only stating a distance but also where you are going (the direction). Other examples, such as velocity and force, depend on direction to completely understand the behavior and effects of those quantities in a physical context. Therefore, vectors are essential in physics, particularly when analyzing motion and forces.
Examples & Analogies
Imagine you're in a large park and you walk 5 kilometers North. If someone just asks you how far you walked, you would say 5 kilometers (which is a scalar). However, if they need to find you, knowing you walked North is critical; you could be anywhere if direction isn't specified! This direction gives context and meaning to your movement, just like vector quantities give context in physics.
Representing Vectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Vectors are often represented graphically by arrows:
- The length of the arrow represents the magnitude of the vector (e.g., a longer arrow means a greater force).
- The direction of the arrow represents the direction of the vector.
- The tail of the arrow is the starting point, and the head (arrowhead) points in the direction.
Detailed Explanation
In physics, vectors can be visually represented using arrows. The length of the arrow symbolizes how large or powerful the vector is, while the direction in which the arrow points shows you where the vector is heading. For instance, an arrow representing a force may be longer if the force is greater. Illustrating vectors this way makes it easier to understand how they interact with one another and how they affect physical systems.
Examples & Analogies
Think of GPS navigation. When you set a course from one location to another, not only is there a distance to cover (magnitude) but also a specific route to follow (direction). Using arrows on a map can help visualize this route - a long arrow suggests a long drive or flight, while its direction indicates where you need to go. Vectors in physics similarly guide the way forces and movements behave.
Understanding Scalars vs Vectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Understanding the difference between scalars and vectors is essential for correctly analyzing physical situations and solving problems, especially when dealing with motion, forces, and fields.
Detailed Explanation
Differentiating between scalars and vectors allows for accurate interpretation and problem-solving in physics. Scalars provide simple measurements that don't involve direction, while vectors offer insight into how quantities like motion and force act in the world. Recognizing when to apply one form or the other is crucial in equations and scenarios involving physics principles. This distinction shapes the fundamental understanding of various physical concepts and their applications.
Examples & Analogies
Consider driving a car. Knowing your speed (a scalar) is important, but knowing your velocity (a vector) tells you how fast you're going and in what direction - crucial information for safe navigation! Understanding both aspects forms a complete picture of your travel situation, just as it does in physics.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Scalar Quantities: Defined by magnitude alone and not direction.
-
Vector Quantities: Defined by both magnitude and direction.
-
Displacement: A vector showing change in position with direction.
-
Velocity: A vector quantifying speed and direction of movement.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A car's speed of 60 km/h is a scalar because it only provides magnitude.
-
A car's velocity of 60 km/h north is a vector as it includes direction.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Scalars are simple as they only need size; vectors need direction, that's the wise!
📖 Fascinating Stories
-
Once a lone rock traveled down a mountain with a mass of 5 kg (scalar). After rolling, it landed 20 meters northeast (vector) from its starting point and gained speed, illustrating both kinds of quantities!
🧠 Other Memory Gems
-
S for Scalar, S for Size—only needs a number, that's how it flies! V for Vector, V for Voyage—needs direction to make a choice.
🎯 Super Acronyms
Remember SVM
- S: for Scalars are Magnitude
- V: for Vectors include direction.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Scalar Quantity
Definition:
A physical quantity completely defined by its magnitude alone.
-
Term: Vector Quantity
Definition:
A physical quantity defined by both magnitude and direction.
-
Term: Magnitude
Definition:
The size or amount of a quantity.
-
Term: Direction
Definition:
The line along which something moves, points, or aims.
-
Term: Displacement
Definition:
A vector quantity that refers to the overall change in position of an object.
-
Term: Velocity
Definition:
A vector quantity that describes the rate of change of position with respect to time.

