Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.

Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.

Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Precision and Accuracy
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Today, we are going to discuss precision and accuracy. Can anyone tell me what accuracy means?

Isn't accuracy about how close a measurement is to the true value?

Exactly, great job! Accuracy refers to how close a measured value is to the accepted true value. Now, how would you define precision?

I think precision has to do with how consistent measurements are with each other.

Yes! Precision indicates how closely multiple measurements agree with each other. Let’s consider a dartboard analogy to understand this. What do you think of that?

Is it like if all darts hit the bullseye, they’re both precise and accurate?

Exactly! That's the perfect representation. Now, if the darts cluster in one area but miss the bullseye, they are precise but not accurate. Excellent! Any other thoughts on this?

That makes sense! What happens if the darts are all over the place?

In that case, they are neither accurate nor precise. Remember, precision is about consistency, while accuracy is about correctness.

To sum it up, accuracy is how close a measurement is to the true value, while precision reflects the closeness of repeated measurements to one another.
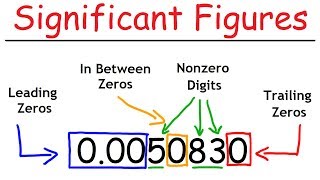
Significant Figures
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Now that we understand precision and accuracy, let’s dive into significant figures. Who can explain what significant figures are?

I think they are the digits that carry meaning contributing to its precision.

Exactly! Significant figures reflect how much certainty is in a measurement. Can anyone tell me the rules for identifying significant figures?

Non-zero digits are always significant.

That’s right! Also, zeros between non-zero digits are significant. But what about leading zeros?

Leading zeros are not significant; they are just placeholders!

Good! Trailing zeros can be tricky too. If there’s a decimal point, they are significant, but if there isn’t, they are not.

So how do we use significant figures in calculations?

In multiplication and division, the final answer should have the same number of significant figures as the measurement with the fewest significant figures; in addition and subtraction, it should match the measurement with the least decimal places.

Let's remember: significance shows reliability in measurements, guiding the precision with which we report our results.
Scientific Notation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Finally, we’ll discuss scientific notation. Why do you think we need it?

I guess it helps shorten complex numbers!

Exactly! This notation makes it easier to write very large or very small numbers in a concise form. What does the scientific notation look like?

It follows the format `a x 10^b`, right?

Yes! Where `a` is between 1 and 10, and `b` is the exponent indicating the power of 10. Can you give me an example of a large number in scientific notation?

Sure! The speed of light is about 300,000,000 m/s, which is `3 x 10^8 m/s`.

Great! And can anyone provide a small number in scientific notation?

The mass of an electron is `9.11 x 10^(-31) kg`!

That’s perfect! Remember, scientific notation is not just a shortcut; it helps preserve significant figures and improves clarity in scientific communication.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Understanding precision and accuracy is vital for making reliable measurements in science. Significant figures communicate the precision of these measurements, while scientific notation simplifies the representation of very large or very small numbers, enhancing clarity and understanding.
Detailed
Precision, Accuracy, Significant Figures, and Scientific Notation
Understanding the precision and accuracy of measurements is essential in science as they define the reliability and trustworthiness of quantitative data. Accuracy refers to how closely a measured value aligns with a true or accepted value, while precision denotes the reproducibility or consistency of measurements, indicating the degree to which repeated measurements yield similar results.
To illustrate these concepts, consider the analogy of darts thrown at a target. If all darts cluster tightly around the bullseye, the measurements are both precise and accurate. If they cluster in the upper left area, they are precise but not accurate. If they are dispersed yet average around the bullseye, they reflect high accuracy yet low precision.
Significant figures convey the precision of a measurement by indicating which digits are meaningful. The rules for determining significant figures include understanding which digits are significant, recognizing leading and trailing zeros, and learning how to handle significant figures in calculations. When conducting arithmetic operations, the result's precision is generally limited by the least precise measurement involved.
Scientific notation serves as an efficient method to express very large or small numbers, maintaining an easily interpretable format such as a × 10^b, where a is a number between 1 and 10, and b is an integer indicating the power of 10. This notation not only allows for simple numerical expressions but also reveals the number of significant figures contained within a measurement, thereby enhancing clarity and utility in scientific communication.
Youtube Videos


Audio Book
Dive deep into the subject with an immersive audiobook experience.
Precision versus Accuracy
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Precision versus Accuracy:
Accuracy: Refers to how close a measured value is to the true or accepted value of the quantity being measured. If you measure the length of a table known to be exactly 2.00 meters, and your measurement is 2.01 meters, that's a very accurate measurement. High accuracy means minimal systematic error (consistent bias in measurements).
Precision: Refers to the closeness of two or more measurements to each other. It describes the reproducibility or consistency of measurements. If you measure the table three times and get 2.01 m, 2.02 m, and 2.00 m, your measurements are precise (they are close to each other), and also accurate (they are close to the true value). If you get 2.51 m, 2.50 m, and 2.52 m, your measurements are precise but not accurate (they are consistently off the true value). High precision means minimal random error (unpredictable variations).
Detailed Explanation
Accuracy and precision are two key concepts that help us understand how reliable our measurements are. Accuracy tells us if our measurement is close to the true value - for instance, if you know a table is exactly 2.00 meters and you measure it at 2.01 meters, that's considered accurate. Precision, on the other hand, indicates how consistently you can get the same measurement multiple times. If you measure the table and get values like 2.01, 2.02, and 2.00 meters, those readings are close to each other, showing good precision and also accuracy. However, if your measurements are like 2.51, 2.50, and 2.52 meters, they are close to each other but not near the true value, indicating precision without accuracy.
Examples & Analogies
Imagine you're playing darts. If all your darts land in the bullseye, you're both accurate and precise. If your darts are grouped together in one corner but not near the bullseye, you're precise but not accurate. If your darts are all over the board but average out to the bullseye, you're accurate but not precise. To get the best results, you want to hit the bullseye consistently!
Illustrative Analogy: A Dartboard
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Illustrative Analogy: A Dartboard
- Accurate and Precise: All darts land tightly clustered in the bullseye.
- Precise, Not Accurate: All darts land tightly clustered together, but consistently far from the bullseye (e.g., all in the upper left corner).
- Accurate, Not Precise: Darts are spread out across the board, but their average position is near the bullseye.
- Neither Accurate nor Precise: Darts are scattered widely and randomly across the board.
Detailed Explanation
This analogy helps illustrate the difference between accuracy and precision using the familiar dartboard game. When you shoot at a dartboard, where the bullseye represents the true value you're trying to hit, you can see how your darts' positions reflect your accuracy and precision. If your darts are all in the bullseye, you are both accurate and precise. If they are clustered together but away from the bullseye, you are precise but not accurate. This provides a vivid connection to understanding these concepts in a practical sense.
Examples & Analogies
Think of yourself at a carnival trying to win a prize by throwing darts. If all your darts land on the bullseye, you win the prize! If they create a tight group on the left but not close to the bullseye, you've got a good arm for precision but need to refine your aim for accuracy. If it's a scattered mess, it’s a reality check that you need some practice!
Significant Figures
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Significant Figures (Sig Figs or S.F.): Expressing Measurement Reliability
Significant figures are the digits in a measurement that are known with certainty plus one estimated digit. They communicate the precision of a measurement. When you record a measurement, you should only include digits that are significant.
Detailed Explanation
Significant figures are a way of conveying how precise your measurements are. They consist of all the digits that are known accurately in a number, plus one estimated digit. When you're measuring something, the more significant figures you include, the more precise your measurement is perceived to be. It's important to only display those digits that accurately reflect the precision of your measurements, which allows others to understand the reliability of the data.
Examples & Analogies
Imagine you are measuring your height. If you stand against the wall and your height is 1.75 meters, that's your significant figure representation. The '1' and '7' are certain digits, while the '5' is an estimate because perhaps your feet weren't flat. If you also adjusted your measuring tape with decimal points indicating more precise measurements, your significant figures would change based on how accurately you've measured yourself.
Rules for Determining Significant Figures
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Rules for Determining Significant Figures:
- Non-zero digits are always significant.
- Example: 45.87 cm (4 sig figs); 234 g (3 sig figs)
- Zeros between non-zero digits (sandwich zeros) are significant.
- Example: 1005 kg (4 sig figs); 20.03 m (4 sig figs)
- Leading zeros (zeros before non-zero digits) are NOT significant. They are placeholders that show the position of the decimal point.
- Example: 0.0025 s (2 sig figs); 0.0104 m (3 sig figs)
- Trailing zeros (zeros at the end of the number):
- Are significant if the number contains a decimal point.
- Example: 2.00 g (3 sig figs); 10.0 cm (3 sig figs); 50. s (2 sig figs - decimal makes the zero significant)
- Are NOT significant if the number does not contain a decimal point.
- Example: 200 cm (1 sig fig - ambiguous, could be 2 or 3 depending on measurement, but conventionally 1); 2500 kg (2 sig figs)
Detailed Explanation
Understanding the rules for significant figures allows you to determine how reliable your measurements really are. The first rule tells us that all numbers except zero count. If you have zeros in between two significant numbers, they count too. However, leading zeros before the first non-zero number do not count as significant because they are just placeholders. The final rule distinguishes between trailing zeros in whole numbers versus decimal numbers, which can change how we interpret the measurement's precision.
Examples & Analogies
Think of significant figures like the VIP guests at a party. Everyone wants to know how many guest are arriving. The famous people (non-zero digits) are always counted; the friends they brought (zeros between others) are also counted. However, if there's a bouncer who says 'no entry' (leading zeros), they don’t get included. The strict house rules decide if those end zeros count as VIPs or not based on the guest list format.
Calculations with Significant Figures
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Calculations with Significant Figures:
When performing calculations with measured values, the result's precision cannot be greater than the least precise measurement used.
- Multiplication and Division: The result should have the same number of significant figures as the measurement with the fewest significant figures.
- Example: 2.5 cm (2 sig figs) * 3.45 cm (3 sig figs) = 8.625 cm². Rounded to 2 sig figs, the answer is 8.6 cm².
- Addition and Subtraction: The result should have the same number of decimal places as the measurement with the fewest decimal places.
- Example: 12.1 cm (1 decimal place) + 1.25 cm (2 decimal places) = 13.35 cm. Rounded to 1 decimal place, the answer is 13.4 cm.
Detailed Explanation
When you combine measurements in calculations, it's crucial to carry out the proper rounding according to significant figures. For multiplication and division, the final answer can’t have more significant figures than the measurement with the fewest significant figures. In contrast, for addition and subtraction, you consider the decimal places. Maintaining this standard ensures that your results accurately reflect the precision of the measurements you're working with.
Examples & Analogies
Imagine you’re mixing ingredients for a cake. You measure flour (2.5 cups) and sugar (3.45 cups) using different measuring cups. When they combine, you can't sound very confident about your volume precision (8.625 cups); only report as much precision as your least stable measurement—2.5 cups. So you'd adjust to 8.6 cups as your final cake mix volume. For adding decorations later, if some were 12.1 cm long and some were 1.25 cm, you couldn't just report all the crazy decimal places without accounting for how closely you actually measured!
Scientific Notation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Scientific Notation: Simplifying Large and Small Numbers
Scientific notation provides a convenient and unambiguous way to express very large or very small numbers, especially when dealing with significant figures. It follows the format:
a×10b
Where:
- a (the coefficient) is a number greater than or equal to 1 and less than 10 (i.e., 1≤a<10). It contains all the significant figures of the number.
- b (the exponent) is an integer (a whole number).
- A positive exponent indicates a large number (move decimal right).
- A negative exponent indicates a small number (move decimal left).
Detailed Explanation
Scientific notation is a method of writing numbers that makes it easier to deal with very large or small values. By expressing a number as a product of a coefficient (which is always between 1 and 10) times ten raised to a power, you simplify the representation. The exponent indicates how many places to move the decimal point: to the right for larger numbers and to the left for smaller numbers.
Examples & Analogies
Think of scientific notation like a light switch. If the number is big like a stadium's seating capacity ( 300,000 people), you simplify it to 3 x 10^5, representing that 3 times 10 repeated five times makes 300,000. For something tiny, like the mass of an electron (0.000000000000000000000000000000911 kg), you might say it's 9.11 x 10^-31 kg, which makes it clearer than a string of zeros!
Examples of Scientific Notation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Examples:
- Large Number: The speed of light is approximately 300,000,000 m/s.
- In scientific notation (with 1 significant figure): 3×10^8 m/s
- If measured more precisely as 299,792,458 m/s (9 sig figs), it would be
2.99792458×10^8 m/s. - Small Number: The mass of an electron is approximately 0.000000000000000000000000000000911 kg.
- In scientific notation (with 3 significant figures): 9.11×10^-31 kg.
Detailed Explanation
Expressing numbers in scientific notation allows us to present them clearly without dealing with unwieldy zeros. For example, the speed of light is commonly expressed as 300 million meters per second (300,000,000 m/s) – in scientific notation, we simplify that to 3 x 10^8 m/s, which is much easier to work with. Similarly, when noting the mass of tiny particles like the electron, scientific notation helps convey very small quantities efficiently.
Examples & Analogies
Imagine you're preparing for a mission to Mars. You have to calculate distances across the solar system. Instead of writing out numbers that look like a long train of zeros, like 300 million kilometers, you'd express it as 3 x 10^8 km, making your calculations quicker and clearer. For things like the weight of a sugar grain (0.0000000000001 kg), you'd simply say '1 x 10^-13 kg!'
Ambiguity with Significant Figures
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Ambiguity with Significant Figures:
The number 5000:
- If it has 1 sig fig: 5×10^3
- If it has 2 sig figs: 5.0×10^3
- If it has 3 sig figs: 5.00×10^3
- If it has 4 sig figs: 5.000×10^3 Scientific notation clearly indicates the number of significant figures.
Detailed Explanation
Significant figures can sometimes lead to ambiguity in measurement, especially with numbers like 5000. Depending on how you express this number, it can convey varying degrees of precision. For instance, saying 5 x 10^3 implies only one significant figure, while adding a decimal point changes it to two significant figures. This understanding ensures that proper precision is conveyed in scientific communication.
Examples & Analogies
Think of it like a cake recipe. If you simply say you need '5000 grams' of flour, one might understand it as roughly 'about 5000', not knowing how accurate you need to be. If you say '5.0 x 10^3 grams', it's clear you're precise about your ingredient amount for the perfect cake—or else, it could turn out dense!
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Accuracy: How close a measurement is to the true value.
-
Precision: Consistency of multiple measurements.
-
Significant Figures: Digits indicating the precision of a measurement.
-
Scientific Notation: A concise format for very large or small numbers.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Large Number: The speed of light is approximately 300,000,000 m/s.
-
In scientific notation (with 1 significant figure): 3×10^8 m/s
-
If measured more precisely as 299,792,458 m/s (9 sig figs), it would be
-
2.99792458×10^8 m/s.
-
Small Number: The mass of an electron is approximately 0.000000000000000000000000000000911 kg.
-
In scientific notation (with 3 significant figures): 9.11×10^-31 kg.
-
Detailed Explanation: Expressing numbers in scientific notation allows us to present them clearly without dealing with unwieldy zeros. For example, the speed of light is commonly expressed as 300 million meters per second (300,000,000 m/s) – in scientific notation, we simplify that to 3 x 10^8 m/s, which is much easier to work with. Similarly, when noting the mass of tiny particles like the electron, scientific notation helps convey very small quantities efficiently.
-
Real-Life Example or Analogy: Imagine you're preparing for a mission to Mars. You have to calculate distances across the solar system. Instead of writing out numbers that look like a long train of zeros, like 300 million kilometers, you'd express it as 3 x 10^8 km, making your calculations quicker and clearer. For things like the weight of a sugar grain (0.0000000000001 kg), you'd simply say '1 x 10^-13 kg!'
-
--
-
Chunk Title: Ambiguity with Significant Figures
-
Chunk Text: ### Ambiguity with Significant Figures:
-
The number 5000:
-
If it has 1 sig fig: 5×10^3
-
If it has 2 sig figs: 5.0×10^3
-
If it has 3 sig figs: 5.00×10^3
-
If it has 4 sig figs: 5.000×10^3 Scientific notation clearly indicates the number of significant figures.
-
Detailed Explanation: Significant figures can sometimes lead to ambiguity in measurement, especially with numbers like 5000. Depending on how you express this number, it can convey varying degrees of precision. For instance, saying 5 x 10^3 implies only one significant figure, while adding a decimal point changes it to two significant figures. This understanding ensures that proper precision is conveyed in scientific communication.
-
Real-Life Example or Analogy: Think of it like a cake recipe. If you simply say you need '5000 grams' of flour, one might understand it as roughly 'about 5000', not knowing how accurate you need to be. If you say '5.0 x 10^3 grams', it's clear you're precise about your ingredient amount for the perfect cake—or else, it could turn out dense!
-
--
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Precision is neat, accurate's the beat, close to the truth, that's how we measure our feet!
📖 Fascinating Stories
-
Imagine a skilled archer. In one competition, her arrows hit all around the bullseye - she's accurate but not precise. In another, they land all in the same corner - she's precise but not accurate. It’s understanding both that makes a champion.
🧠 Other Memory Gems
-
To remember Significant Figures: Just recall 'None Zeroes, Inside or Ending!' - Non-zero digits are significant, zeros in between are too, trailing zeros count if there's a decimal!
🎯 Super Acronyms
For Scientific Notation
- 'A Coefficient
- Moved Power' (A = a in a×10^b). This reminds you of the two crucial parts!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Accuracy
Definition:
The degree to which a measured value corresponds to the true value.
-
Term: Precision
Definition:
The closeness of two or more measurements to each other.
-
Term: Significant Figures
Definition:
Digits in a measurement that are known with certainty plus one estimated digit, indicating measurement precision.
-
Term: Scientific Notation
Definition:
A method of expressing numbers as a product of a coefficient and a power of ten.

