Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Linear Equations
Unlock Audio Lesson

Welcome class! Today we'll be discussing linear equations. Can anyone tell me what you think a linear equation is?

I think it's about relationships in math. Like how things change together?

Yeah! Like how cost goes up with more items.

Great observations! A linear equation indeed describes relationships that have a constant rate of change. For example, if you buy more copies of a book, the total price increases linearly!

So it forms a straight line on a graph?

Exactly! When plotted, these equations form straight lines on a coordinate plane. Remember, linear means 'line' in Latin.

What do the 'a', 'b', and 'c' mean in the equations?

Great question! In the form ax + b = 0, 'a' is the coefficient representing the slope, and 'b' is the constant. In the two-variable equation ax + by = c, 'a', 'b', and 'c' are real numbers. Do you want to know more about how these parts work together?

Yes, please!
Examples of Linear Equations
Unlock Audio Lesson

Let’s look into some examples! Who can give me the general form of a linear equation in one variable?

Is it like ax + b = 0?

That's right! And what about in two variables?

Um, ax + by = c?

Perfect! Let’s compute a basic example. If we have 3x - 7 = 11, what would be our first step?

Add 7 to both sides!

Correct! This gives us 3x = 18, what do we do next?

Divide by 3 to get x = 6?

Exactly! You’re all doing great. Remember to substitute back to check your solution.
Applications of Linear Equations
Unlock Audio Lesson

Now that we understand linear equations, let’s talk about where we see them in real life. Can anyone think of an example?

What about budgeting?

Excellent! If a phone plan costs $10 plus an extra $0.50 for every minute, how can we write this as a linear equation?

C = 0.5m + 10, right?

Correct, C is the total cost and m is the minutes used. Linear equations can model many situations, like motion and profit calculations.

How do you interpret those equations?

By analyzing what the slope and intercept represent in each context! And remember, the slope indicates how steep that relationship is.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
A linear equation is defined as an equation where each term is either a constant or involves a single variable, resulting in a straight line on a graph. They can be represented in one or two variables, allowing for various methods of solving and interpreting real-world problems.
Detailed
In mathematics, a linear equation is an algebraic formulation that outlines a relationship where the power of the variables involved is one. It can be expressed in the general form of a single variable equation as ax + b = 0, and for two variables as ax + by = c, where a, b, and c are real numbers. When plotted on a coordinate plane, these equations yield straight lines. Understanding linear equations is crucial in algebra as they represent countless real-world scenarios, from budgeting to scientific calculations. They serve as a foundation for more advanced concepts in algebra and mathematics, enabling students to develop problem-solving skills and appreciation for mathematical relationships.
Example
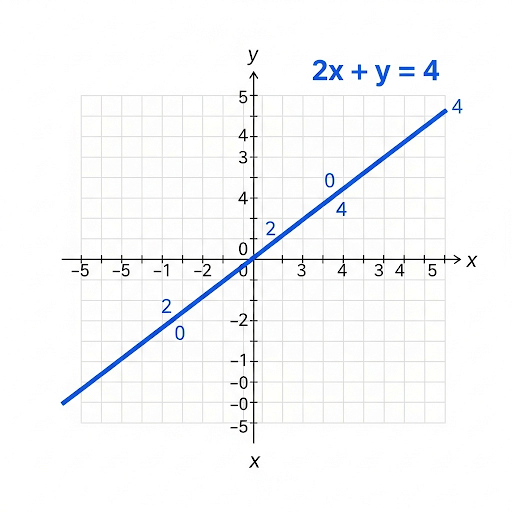
The equation 2x + y = 4 is a linear equation in two variables.
To find solutions, you can choose a value for one variable and solve for the other. For instance:
If x = 1, then 2(1) + y = 4, which means 2 + y = 4, so y = 2. A solution is (1, 2).
If x = 0, then 2(0) + y = 4, which means 0 + y = 4, so y = 4. A solution is (0, 4).
Plotting these points and connecting them with a straight line gives you the graph of the equation.
Youtube Videos



Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of a Linear Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable. It forms a straight line when graphed on a coordinate plane.
Detailed Explanation
A linear equation represents a relationship where the highest power of the variable is one. This means that it doesn’t involve squared, cubed, or higher powers of the variable. When we graph a linear equation on a coordinate plane, the result is a straight line. This straight line shows how one variable changes in relation to the other.
Examples & Analogies
Imagine you are running straight on a track. Your distance from the starting point can be represented as a linear equation. If you run at a constant speed, your distance increases in a straight line over time, similar to how a linear equation works.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Linear Equation: A fundamental algebraic equation with a constant rate of change.
-
Slope: Indicates the steepness or angle of the line on a graph.
-
Y-Intercept: The y-coordinate where the line intersects the y-axis.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: Solve 3x - 7 = 11. Solution: x = 6.
-
Example 2: Write the equation for a taxi that charges $5 plus $2 per kilometer.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Line upon line, straight and true, ax and by will guide you through.
📖 Fascinating Stories
-
Once upon a time, a taxi driver charged a base fee and a per-mile rate. His fares kept track on a graph, forming a straight line through all the rides.
🧠 Other Memory Gems
-
For the slope and intercept, remember 'S' for slope and 'I' for intercept when using the equation y = mx + b.
🎯 Super Acronyms
To recall ax + by = c, think 'A,B,C' for 'All Before Change'.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Linear Equation
Definition:
An algebraic equation where each term is either a constant or the product of a constant and a single variable.
-
Term: Slope
Definition:
The rate of change of a line represented in a linear equation, usually denoted as 'm'.
-
Term: YIntercept
Definition:
The point where a line crosses the y-axis, represented as 'c' in slope-intercept form.
Short Quiz
Q1. Which of the following is a linear equation in two variables?
a) \(x^2 + y = 5\)
b) \(2x + 3y = 6\)
c) \(xy = 4\)
d) \(y^2 - x = 7\)
Answer: b) \(2x + 3y = 6\)
Q2. What is the slope of the line represented by the equation \(4x + y = 12\)?
a) 4
b) -4
c) 12
d) \(\tfrac{1}{4}\)
Answer: b) -4
Q3. If the cost of a taxi ride is given by \(C = 5 + 2d\), where \(d\) is the distance in km, what does the number 5 represent?
a) Cost per km
b) Base fare
c) Total cost
d) Distance traveled
Answer: b) Base fare
Q4. How many solutions does the linear equation \(3x - 7 = 11\) have?
a) None
b) One
c) Two
d) Infinitely many
Answer: b) One
Q5. Which equation will form a vertical line?
a) \(y = 3x + 2\)
b) \(x = 5\)
c) \(y = -4\)
d) \(2x + y = 6\)
Answer: b) \(x = 5\)
