Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Quadratic Functions
Unlock Audio Lesson

Today we’re discussing quadratic functions. What do you think defines such a function?

Is it an equation with an x_squared term?

Exactly! The general form is $$f(x) = ax^2 + bx + c$$. Here, a, b, and c are constants and crucial for the shape of the graph. Can anyone tell me what restrictions we have on 'a'?

It cannot be zero!

Correct! If a is zero, it wouldn't be a quadratic function. Remember that the sign of 'a' affects the direction the parabola opens: upwards if positive and downwards if negative.

I remember that with the acronym U for up and D for down!

Fantastic! That’s a great mnemonic.
Graphing and Features of Quadratic Functions
Unlock Audio Lesson

Now that we know the form of quadratic functions, let's discuss their graph properties. What can you find about the vertex?

It’s the highest or lowest point of the graph, right?

Exactly right! The vertex can be calculated using $$x = -\frac{b}{2a}$$, and then you plug this x value into the function to find y. Who remembers what the axis of symmetry is?

It's the line that goes through the vertex, isn't it?

Yes! It's given by $$x = -\frac{b}{2a}$$ too. And the intercepts can be found by substituting for x and y. Can you all recall how to do that?

We set x to zero for y-intercepts and solve for x when y is zero for x-intercepts!

Perfect! Great teamwork.
Solving Quadratic Equations
Unlock Audio Lesson

Let’s dive into solving quadratic equations. What do you think of using factoring as a method?

It’s like breaking it down into two simpler equations!

Exactly! We express it as $$ax^2 + bx + c = (dx + e)(fx + g)$$, and set each factor to zero. Does anyone know another method?

Completing the square! Like transforming it to the vertex form!

Right! After we complete the square, we can derive the maximum or minimum values easily. Last method involves a formula; who remembers its name?

Quadratic formula! $$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$!

Great job! Remember that the discriminant will help us determine the nature of the roots based on whether it’s positive, zero, or negative.
Real-Life Applications of Quadratic Functions
Unlock Audio Lesson

Finally, let's connect quadratics to real life. Can anyone think of where we've seen quadratics in the real world?

Projectile motion, like how balls are thrown!

Yes! That's a classic example. Any other scenarios?

In economics, we talk about maximizing profit using quadratics.

Absolutely! Understanding the maximum and minimum values helps businesses make critical decisions.

And in engineering, arches and structures often use parabolic shapes, right?

Exactly! Quadratic functions are not only mathematical constructs but also essential in the real world. Keep these applications in mind as they can help solidify your understanding.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this chapter summary, we explore the fundamental components of quadratic functions, which take the form ax² + bx + c, the properties of their graphs (parabolas), and the various methods for solving quadratic equations such as factoring, completing the square, and using the quadratic formula.
Detailed
Chapter Summary
This chapter covers essential aspects of quadratic functions, a vital part of algebra. The general form of a quadratic function is given as:
General Form
$$f(x) = ax^2 + bx + c$$
where a, b, and c are real numbers and a ≠ 0. The significance of this chapter lies in its comprehensive exploration of quadratic functions, including:
- Graph Representation: The graph of a quadratic function is a parabola which opens upwards if a > 0 and downwards if a < 0. Important points include the vertex, axis of symmetry, and x- and y-intercepts.
- Vertex and Axis of Symmetry: The vertex represents the maximum or minimum point of the parabola and is derived using the formula; the axis of symmetry can be calculated from the vertex coordinates.
- Methods of Solving Quadratic Equations: Three primary methods include factoring, completing the square, and the quadratic formula. Understanding the discriminant (Δ) helps to determine the type of roots a quadratic equation has.
- Real-Life Applications: Quadratic functions have practical relevance in physics (e.g., projectile motion), economics (maximizing profit), and engineering (structural designs). The versatility of quadratics makes them crucial in various fields.
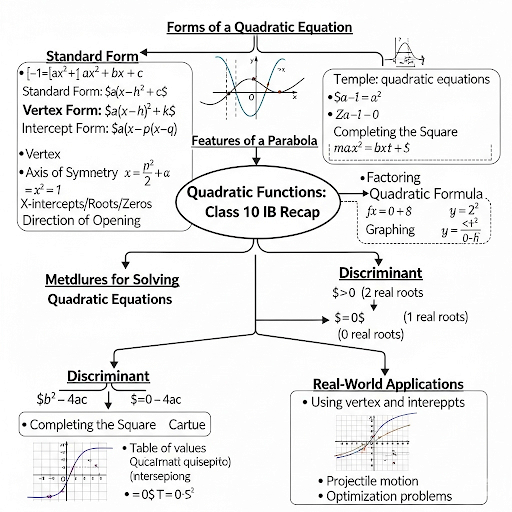
Conclusively, the chapter emphasizes the multifaceted applications and underlying principles of quadratic functions, preparing students for more advanced mathematical concepts.
Audio Book
Dive deep into the subject with an immersive audiobook experience.
General Form of Quadratic Function
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A quadratic function has the general form 𝑎𝑥² + 𝑏𝑥 + 𝑐.
Detailed Explanation
A quadratic function is a special type of polynomial function where the highest exponent of the variable is 2. This means it has a squared term (𝑎𝑥²), a linear term (𝑏𝑥), and a constant (𝑐). In this expression, the coefficients 𝑎, 𝑏, and 𝑐 can be any real numbers, but 𝑎 cannot be zero since that would make it a linear function instead of quadratic.
Examples & Analogies
Think of the quadratic function 𝑓(𝑥) = 2𝑥² + 3𝑥 + 1 as a recipe. The term 2𝑥² represents the main ingredient that gives the most flavor (the dominant term), while 3𝑥 adds some seasoning (the effect of changing 𝑥), and the 1 is just a little pinch of salt (a constant that doesn’t change as you mix other ingredients).
Graphical Representation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The graph is a parabola, opening up or down depending on the sign of 𝑎.
Detailed Explanation
The graph of any quadratic function is called a parabola. If the coefficient 𝑎 is positive (i.e., 𝑎 > 0), the parabola opens upward, resembling a bowl. If 𝑎 is negative (i.e., 𝑎 < 0), it opens downward, looking like a frown. This characteristic is essential in predicting the nature of the graph based on the function's equation.
Examples & Analogies
Imagine a roller coaster. When the first incline leads upwards, you have an ascending curve like an upward-opening parabola. When it descends sharply on the other side, it's like a downward-opening parabola, demonstrating how these curves can mimic the shapes we see in real structures or trajectories.
Key Features of Quadratics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Key features: vertex, axis of symmetry, x- and y-intercepts.
Detailed Explanation
Every quadratic equation has specific features, including the vertex, which is the highest or lowest point of the parabola depending on its direction. The axis of symmetry is a vertical line that divides the parabola into two mirror-image halves, passing through the vertex. Additionally, the x- and y-intercepts show where the graph crosses the axes, giving vital information about the function's solutions and behavior.
Examples & Analogies
Think of the vertex as the peak of a mountain. The axis of symmetry is like a path that leads up to the peak and branches out equally on both sides. The intercepts are like where trails meet different routes, showing how the mountain (or function) interacts with the ground (or axes) at specific points.
Methods for Solving Quadratic Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Solve quadratic equations using: factoring, completing the square, quadratic formula.
Detailed Explanation
There are three primary methods to solve quadratic equations. The factoring method allows us to express the equation in a product form, making it easy to find the roots. Completing the square transforms the equation into a perfect square trinomial, helping us find solutions. The quadratic formula provides a direct way to find roots using the coefficients of the equation, ensuring we can solve any quadratic regardless of its complexity.
Examples & Analogies
Imagine trying to fix a broken object. Factoring is like taking the object apart to see its components, while completing the square is like reorganizing the pieces; both methods help you see how to put it back together. Using the quadratic formula is like having a toolkit that provides you with the right tools for any job, ensuring you can tackle problems efficiently.
Understanding the Discriminant
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The discriminant helps determine the nature of the roots.
Detailed Explanation
The discriminant is calculated using the formula 𝛥 = 𝑏² - 4𝑎𝑐 from the quadratic equation. It provides crucial information about the solutions: if 𝛥 > 0, there are two distinct real roots; if 𝛥 = 0, there is one real root (the vertex touches the x-axis); and if 𝛥 < 0, there are no real roots, only complex solutions. This information helps us predict the behavior of the function graphically.
Examples & Analogies
Think of the discriminant as a weather forecast for a day out. If the forecast predicts sunny conditions (𝛥 > 0), you can expect a pleasant outing. If it shows cloudy with a chance of rain (𝛥 = 0), it's a good idea to keep an umbrella handy. But if it's all stormy (𝛥 < 0), it’s better to stay indoors, as the function in this case won't cross the x-axis at all.
Real-Life Applications of Quadratics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Quadratics are used in various real-life contexts, especially involving maximum and minimum values.
Detailed Explanation
Quadratic functions have numerous practical applications. They model different real-world phenomena like projectile motion, where the path of a thrown object (like a ball) follows a parabola. Additionally, in economics, they help optimize profit or minimize costs. Understanding quadratics allows us to solve problems where we need to determine the best outcome, whether it's maximizing resources, profits, or time.
Examples & Analogies
Think of a project that requires maximizing a garden's area (product) under certain constraints (materials). Using quadratic functions is like figuring out the best shape to get the most space for planting while using the least materials, similar to how nature naturally organizes plants for efficiency.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Quadratic Function: Defined as a function of the form ax² + bx + c where a ≠ 0.
-
Vertex: The point of maximum or minimum value of a quadratic function, key to determining the shape of the graph.
-
Axis of Symmetry: A vertical line passing through the vertex, crucial for graph sketching.
-
X-Intercepts: The roots of the equation where the curve intersects the x-axis.
-
Y-Intercept: The value of the function when x = 0, important for understanding graph position.
-
Discriminant: A determinant that gives insight into the number and type of roots.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of Factoring: Solve x² + 5x + 6 = 0 leads to (x+2)(x+3)=0 hence x = -2 or -3.
-
Example of Completing the Square: Solving x² + 4x + 1=0 gives (x + 2)² - 3 = 0 leading to x = -2 ± √3.
-
Example using Quadratic Formula: From 2x² - 4x - 6 = 0, we deduce solutions x = 3 and x = -1.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
For each quadratic, look for A, B, C, the graph will show you where it will be.
📖 Fascinating Stories
-
Imagine a ball soaring upwards; it reaches its peak point encapsulating the vertex, then falls down creating a parabola.
🧠 Other Memory Gems
-
Use 'VAX' to remember: Vertex, Axis, x-intercepts, for quadratics!
🎯 Super Acronyms
Remember 'FCS' for methods
- Factoring
- Completing the Square
- and using the Quadratic formula.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Quadratic Function
Definition:
A polynomial function of degree 2, expressed as f(x) = ax² + bx + c.
-
Term: Vertex
Definition:
The maximum or minimum point of a parabola.
-
Term: Axis of Symmetry
Definition:
A vertical line that divides the parabola into mirror-image halves.
-
Term: XIntercepts
Definition:
The points where the graph crosses the x-axis, found by setting f(x) = 0.
-
Term: YIntercept
Definition:
The point where the graph intersects the y-axis, found by evaluating f(0).
-
Term: Discriminant
Definition:
The expression b² - 4ac, which determines the nature of the roots.
