Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Quadratic Functions
Unlock Audio Lesson

Welcome class! Today, we are diving into the world of quadratic functions. Can anyone remind me what the general form of a quadratic function is?

Is it \( f(x) = ax^2 + bx + c \)?

Excellent! That's correct. Now, let's remember that \( a, b, \) and \( c \) are real numbers, with \( a \) not being zero. Do you know why it can't be zero?

Because if \( a \) were zero, it wouldn't be a quadratic function anymore?

Exactly! Without that \( a \), we'd just have a linear function. Now, let's also discuss the graph of a quadratic function—do you know what it looks like?

It's a parabola, right? It can open either up or down.

That's right! The direction the parabola opens depends on the sign of \( a \); if \( a > 0 \), it opens upwards, and if \( a < 0 \), it opens downwards.

What about the vertex of the parabola?

Great question! The vertex is the maximum or minimum point of the parabola. We can find the x-coordinate of the vertex using the formula \( x = -\frac{b}{2a} \). Let’s remember to memorize that formula with the acronym VAM, which stands for 'Vertex Axis Maximum'! Any questions so far?

Can you explain the axis of symmetry?

Sure! The axis of symmetry is the line that vertically cuts the parabola into two mirror images. It can be found using the same value \( x = -\frac{b}{2a} \). So today, remember: VAM is your key to recalling the vertex and axis of symmetry. To summarize, quadratic functions have a specific structure, result in a parabola, and key points include the vertex and axis of symmetry.
Methods of Solving Quadratic Equations
Unlock Audio Lesson

Now that we understand the basics of quadratic functions, let's explore how to solve them! One method is by factoring. Who remembers how to factor a quadratic equation?

You can express it in the form of two binomials like \((dx + e)(fx + g) = 0\) and then solve for x.

Exactly! And what do we do once it's factored?

Set each factor equal to zero and solve for x.

Correct! Now, let's move on to another method: completing the square. Anyone heard of this technique?

Yes! You reorganize the quadratic to get a perfect square trinomial.

Great! The formula to complete the square is \( a(x + d)^2 + e \). Can anyone give me an example of a quadratic that we can complete to the square?

How about \( x^2 + 6x + 5 \)?

Perfect choice! If we complete the square, we find it's \((x + 3)^2 - 4\). Now, let’s also touch on the quadratic formula as another method. It’s a powerful tool. Does anyone know the formula?

It's \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \)!

Exactly! And it’s especially helpful when the quadratic can't be easily factored. Remember the discriminant part too; it tells us about the nature of the roots. Can anyone summarize our methods?

We can solve quadratics using factoring, completing the square, or the quadratic formula!

Great recap! Remember these methods because we will use them in our practice problems.
Applications of Quadratic Functions
Unlock Audio Lesson

Now class, let’s discuss the applications of quadratic functions. They aren’t just numbers and formulas! Can anyone give an example of where we might see quadratics in real life?

Projectile motion, like when throwing a ball?

Exactly! The height of a ball thrown can be modeled by a quadratic equation. What happens at the top of the ball's path?

That would be the maximum height!

Correct! And how about in economics?

Quadratics can help maximize profits or minimize costs!

Exactly; businesses use quadratics to determine optimal pricing. Can anyone think of an engineering application?

I think in designing structures, like bridges, parabolic shapes are used.

Great example! Recall that understanding quadratics is not just theoretical. In summary, quadratics are used in physics, economics, and engineering, among other fields!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section introduces quadratic functions, highlighting their standard form, properties, and significance in both theoretical and practical aspects of mathematics. The importance of quadratic functions in various domains like physics and economics is discussed.
Detailed
Detailed Summary
Quadratic functions are a key component of algebra, fundamental to the IB Mathematics curriculum and beyond. Expressed in the form \( f(x) = ax^2 + bx + c \), where \( a, b, \) and \( c \) are real numbers and \( a \neq 0 \), these functions represent polynomial behavior of degree 2. The graph of a quadratic function is a parabola, which has critical features including the vertex (the highest or lowest point), the axis of symmetry, and the intercepts on both x and y axes. 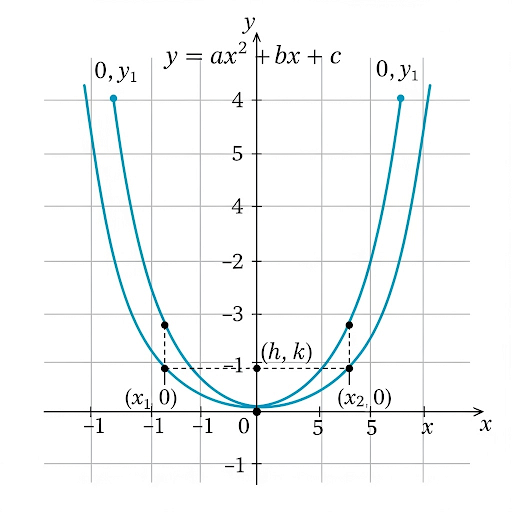
In this chapter, we will explore various aspects of quadratic functions, including their structural characteristics, methods for solving quadratic equations (factoring, completing the square, and the quadratic formula), and how to utilize these equations graphically. Furthermore, we will delve into their real-life applications such as projectile motion in physics or optimization in economics. Understanding these foundations will provide essential skills and insights valuable in multiple fields.
Youtube Videos

Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Quadratic Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Quadratic functions are foundational to algebra and a critical part of the IB Mathematics curriculum. They not only appear in various areas of mathematics but also have practical applications in physics, economics, engineering, and architecture.
Detailed Explanation
Quadratic functions are essential mathematical expressions defined as polynomials of degree two. This means their highest exponent is 2, making them distinct and important in mathematical analysis. They are not just limited to theoretical mathematics; their relevance extends to practical applications in various fields, such as physics, where they describe projectile motion, in economics for cost and revenue calculations, in engineering for structural design, and in architecture for curves and structures.
Examples & Analogies
Think of a quadratic function as a tool that can help us understand how things move or change in real life. For instance, if you toss a ball into the air, its height over time can be modeled as a quadratic function. This function makes it possible to predict the ball's highest point and when it will hit the ground.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Quadratic Function: A polynomial function of degree 2, expressed as \( f(x) = ax^2 + bx + c \).
-
Parabola: The graph of a quadratic function, which can open upwards or downwards.
-
Vertex: The highest or lowest point of the parabola, determined using \( x = -\frac{b}{2a} \).
-
Axis of Symmetry: A vertical line through the vertex that divides the parabola into two equal halves.
-
X-Intercept: The points at which the parabola intersects the x-axis, found by solving \( f(x) = 0 \).
-
Y-Intercept: The point where the parabola intersects the y-axis, calculated by evaluating \( f(0) = c \).
-
Discriminant: The expression \( b^2 - 4ac \) used for determining the number of real roots.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of a parabolic equation: If \( f(x) = 2x^2 - 8x + 6 \), the vertex is determined by \( x = -\frac{-8}{2(2)} = 2 \). When you evaluate, you find that the vertex is at the point (2, -2).
-
Using the quadratic formula: If solving for \( 2x^2 - 4x - 6 = 0 \), you can apply the quadratic formula to find the roots as x = 3 and x = -1.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When x is squared and a is found, a parabola is where it's bound!
📖 Fascinating Stories
-
Imagine a ball being thrown up high in the sky, it traces a path shaped like a U. As it reaches the peak, gravity pulls it down, modeling a quadratic journey.
🧠 Other Memory Gems
-
Use VAM to find the vertex and axis means maximum or minimal costs in all our classes!
🎯 Super Acronyms
V.A.M. - Vertex, Axis, Maximum
- helps remember what to calculate when studying quadratics.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Quadratic Function
Definition:
A polynomial function of degree 2, expressed in the form \( f(x) = ax^2 + bx + c \) where \( a \neq 0 \).
-
Term: Polynomial
Definition:
An algebraic expression consisting of variables raised to whole number exponents and their coefficients.
-
Term: Parabola
Definition:
The graphical representation of a quadratic function, which is U-shaped.
-
Term: Vertex
Definition:
The maximum or minimum point of a parabola.
-
Term: Axis of Symmetry
Definition:
A vertical line that divides the parabola into two mirror images, found at \( x = -\frac{b}{2a} \).
-
Term: XIntercept
Definition:
The points where the graph crosses the x-axis; found by solving \( f(x) = 0 \).
-
Term: YIntercept
Definition:
The point where the graph crosses the y-axis; found by evaluating \( f(0) \).
-
Term: Discriminant
Definition:
The value \( b^2 - 4ac \) used to determine the nature of the roots of a quadratic equation.
-
Term: Factoring
Definition:
The process of breaking down a quadratic into the product of two binomials.
-
Term: Completing the Square
Definition:
A method used to convert a quadratic equation into a perfect square trinomial.
