Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Critical Points
Unlock Audio Lesson

Today, we are going to discuss critical points. A critical point occurs where the first derivative of a function is zero or undefined. Do you remember what a derivative indicates?

It measures how a function is changing, right?

Exactly! And when the derivative is zero or undefined, it suggests that the function may have a maximum or minimum point. Why do you think this is important?

It helps us understand the behavior of the function!

Precisely! Remember the acronym **CUP** for Critical points lead to Understanding Peaks (maxima) and Valleys (minima).
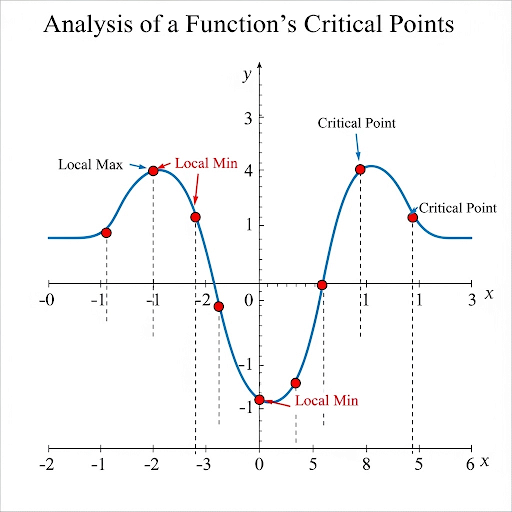
Identifying Turning Points
Unlock Audio Lesson

Now, let’s talk about turning points. What do you think they are?

I think they are points where the function changes direction!

Correct! There are two types of turning points: local maxima and local minima. Can anyone tell me how to identify these using the first derivative?

If the first derivative changes from positive to negative, it's a local maximum, right?

Exactly! And if it changes from negative to positive, that's a local minimum. Keep in mind: **Maxima are at the top, minima are at the bottom.**
Applying the First Derivative Test
Unlock Audio Lesson

Now that we know what critical points and turning points are, let's explore the First Derivative Test. Can someone explain its steps?

We need to find the first derivative and set it to zero to find critical points!

Yes! And what do we do next?

We check if the derivative changes from positive to negative or vice versa.

Perfect! Remember the phrase **Positive to Negative = Peak; Negative to Positive = Pit** to recall the patterns.
Utilizing the Second Derivative Test
Unlock Audio Lesson

Now, let's move on to the Second Derivative Test. Who can summarize when we use this test?

We use it when the first derivative is zero, right?

Exactly! What do we look for with the second derivative?

If it's greater than zero, we have a minimum, and if it's less than zero, we have a maximum!

Exactly! So remember: **Second Derivative = Shape of the Graph.** If it's positive, the graph is concave up, and it's a minimum. If it's negative, concave down, so it's a maximum.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Critical points are where a function's first derivative equals zero or is undefined, indicating potential turning points where the function changes direction. The section emphasizes methods for identifying and classifying these points, including the first and second derivative tests.
Detailed
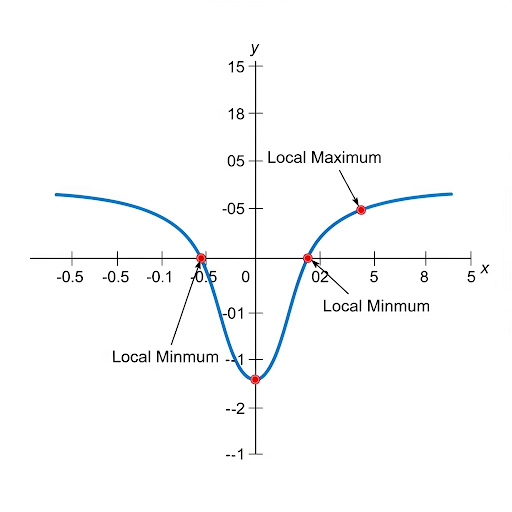
Critical Points and Turning Points
In calculus, critical points of a function, defined as locations where the first derivative is either zero or undefined, are essential in determining the function's local maxima and minima. A turning point signifies a change in direction of the function's graph, essential for optimization problems. This section categorizes turning points into local maxima, where the function peaks locally, and local minima, representing the lowest points locally. The First Derivative Test and Second Derivative Test are introduced as methods for determining the nature of these critical points. Mastery of these concepts is key for solving real-world optimization problems, such as maximizing areas or understanding the behavior of economic models.
Youtube Videos




Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Critical Points
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A critical point of a function 𝑓(𝑥) occurs where the first derivative 𝑓′(𝑥) = 0 or is undefined.
Detailed Explanation
A critical point is a specific location on the graph of a function where the slope is either zero or doesn't exist. This is important because these points could indicate where the function reaches its maximum or minimum values. To find these points, we look for values of x that make the first derivative (which represents the slope of the function) equal to zero or undefined.
Examples & Analogies
Think of a car driving along a hilly road. When the car reaches the peak of a hill (maximum point) or the dip in a valley (minimum point), it may temporarily come to a stop (slope = 0). These points where the car is neither going up nor down correspond to critical points in the function's graph.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Critical Point: A key location in a function's behavior where the derivative is zero or undefined.
-
Turning Point: The point at which a function changes direction.
-
Local Maximum: The peak of a function in a local neighborhood.
-
Local Minimum: The lowest point of a function in a local neighborhood.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example for Maximum: For f(x) = x² - 4x + 3, critical point at x = 2 shows a local minimum at (2, -1).
-
Example for Minimum: For f(x) = -x³ + 3x² + 9, critical points at x = 0 (local min) and x = 2 (local max).
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
If the slope is flat, time to chat; max or min, let's begin!
📖 Fascinating Stories
-
Once upon a time, a little hill stood tall—max at the peak, but fell to the ball.
🧠 Other Memory Gems
-
For maxima think 'M' for mountain—minima think 'V' for valley.
🎯 Super Acronyms
Use **CUM** to remember
- Critical Points give us Up or Down.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Critical Point
Definition:
A point where the first derivative of a function is zero or undefined.
-
Term: Turning Point
Definition:
A point on a graph where the function changes direction.
-
Term: Local Maximum
Definition:
A point where a function reaches a peak locally.
-
Term: Local Minimum
Definition:
A point where a function reaches a valley locally.
-
Term: First Derivative Test
Definition:
A method to determine where a function changes from increasing to decreasing or vice versa.
-
Term: Second Derivative Test
Definition:
A method to determine the concavity of a function to classify local maxima and minima.
🚀 Optimization Problem
A rectangular field is to be fenced on three sides (two widths and one length).
The fourth side will be along a river and does not require fencing.
You have 200 meters of fencing available.
Question:
What dimensions of the field will give the maximum area?
🔎 Step-by-Step Thinking (Interactive Prompts)
- Define variables:
Let the length along the river = \(L\), and the width = \(W\).
👉 Can you express the fencing constraint in terms of \(L\) and \(W\)?
Hint: Only three sides need fencing.
- Form the constraint equation:
The fencing used = \(L + 2W\).
\[
L + 2W = 200
\]
👉 Can you solve this for \(L\) in terms of \(W\)?
- Write the area function:
Area = \(A = L \times W\).
👉 Substitute the value of \(L\) from Step 2 into this equation.
- Simplify the area function:
\[
A(W) = (200 - 2W) \cdot W = 200W - 2W^2
\]
- Find the maximum area using calculus:
-
First derivative:
\[
A'(W) = 200 - 4W
\]
Set \(A'(W) = 0 \Rightarrow 200 - 4W = 0 \Rightarrow W = 50
\] -
Second derivative:
\[
A''(W) = -4 \; (< 0)
\]
So, \(W = 50\) gives a maximum.
- Find corresponding length:
\[
L = 200 - 2W = 200 - 100 = 100
\]
✅ Final Answer
The field will have maximum area when:
\[
L = 100 \; \text{m}, \quad W = 50 \; \text{m}
\]
The maximum area is:
\[
A = 100 \times 50 = 5000 \; \text{m}^2
\]
