Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Classical Probability
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today we’re diving into the classical probability, which is crucial when outcomes are equally likely. Can anyone tell me how we calculate classical probability?
Is it just the number of favorable outcomes divided by the total possible outcomes?
Exactly, well done! To remember this, you can use the phrase 'Favorable over Total'. The formula is \( P(E) = \frac{\text{Number of favorable outcomes}}{\text{Total number of possible outcomes}} \).
What does it mean if an outcome is impossible?
Great question! If an event is impossible, its probability is 0. So we always have \( 0 ≤ P(E) ≤ 1 \).
Can you give us an example?
Of course! Think of rolling a fair die. If I want to know the probability of rolling a 4, that's \( P(4) = \frac{1}{6} \) since there’s one outcome that's favorable over six total possibilities.
That clears things up! Thanks!
To summarize, classical probability relies on equal likelihood and is computed with a simple formula. Remember: 'Favorable over Total'!
Empirical Probability
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let's shift gears to **Empirical Probability**. Who can explain what it is?
Isn't it based on what we've actually observed in experiments?
"Exactly! It relies on real data. The formula is:
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the fundamentals of probability, including its definitions, the classification of probability into classical, empirical, and subjective categories, and the essential properties that dictate probability calculations. Additional focus is on concepts such as complement events, independence, and conditional probability, supported by practical examples and visual tools like Venn diagrams.
Detailed
Detailed Summary
This section, ‘Defining Probability’, delves into the core concepts of probability, a crucial mathematical field that quantifies uncertainty and aids decision-making in various contexts. We start by categorizing probability into three main types:
- Classical (Theoretical) Probability: This is utilized when outcomes are equally likely, calculated by the formula:
\[ P(E) = \frac{\text{number of favorable outcomes}}{\text{total number of possible outcomes}} \]
- Empirical (Experimental) Probability: Based on actual observations, this probability is determined through experimental data:
\[ P(E) = \frac{\text{number of times E occurred}}{\text{total number of trials}} \]
- Subjective Probability: This type relies on personal judgment or experience rather than precise calculations.
The section also outlines essential properties of probability, including:
- Bounds: \( 0≤P(E)≤1 \)
- Complement Rule: \( P(E′) = 1−P(E) \)
- Certain and Impossible Events: With probabilities of 1 and 0, respectively.
- Addition Rule for calculating the probability of two events.
The use of Venn Diagrams is introduced as a visual method to represent probabilities, demonstrating intersections and unions of events.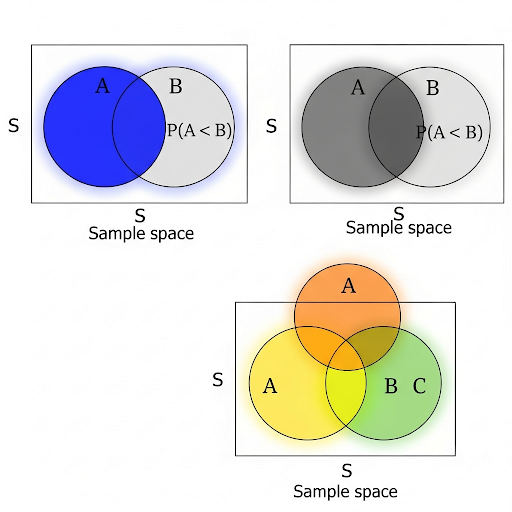
The section is illustrated with a worked example concerning rolling a die. This example highlights how to compute the probabilities of various events, reinforcing concepts through practical application. Moving forward, we touch upon more complex ideas such as conditional probability and the concepts of independent and mutually exclusive events. The narrative concludes with an introduction to Bayes' Theorem and Probability Distributions, setting the stage for deeper exploration in Future sections.
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Classical (Theoretical) Probability
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Applicable when outcomes are equally likely.
\[
P(E) = \frac{\text{number of favorable outcomes}}{\text{total number of possible outcomes}}
\]
Detailed Explanation
Classical probability is used when all outcomes of an experiment are equally likely. For example, when rolling a fair die, each face (1 through 6) has an equal chance of landing face up. The probability of an event (E) can be calculated by dividing the number of favorable outcomes (the outcomes that constitute the event) by the total number of possible outcomes.
Examples & Analogies
Imagine you have a bag with 10 marbles: 4 red and 6 blue. If you want to find the probability of randomly selecting a red marble, you would calculate it as the number of red marbles over the total number of marbles: \( P(Red) = \frac{4}{10} = 0.4 \). This shows you have a 40% chance of picking a red marble.
Empirical (Experimental) Probability
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Based on observed data.
\[
P(E) = \frac{\text{number of times E occurred}}{\text{total number of trials}}
\]
Detailed Explanation
Empirical probability, also known as experimental probability, is determined by conducting an experiment and observing the outcomes. To find the probability of an event (E) using empirical methods, you count how many times the event occurs and divide that by the total number of trials or experiments conducted.
Examples & Analogies
If you were to flip a coin 100 times and it lands on heads 56 times, the empirical probability of getting heads would be calculated as \( P(Heads) = \frac{56}{100} = 0.56 \). This demonstrates a 56% chance of landing heads based on your observed data.
Subjective Probability
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Assessed on judgments or experience rather than strict calculation.
Detailed Explanation
Subjective probability is based on personal judgment, intuition, or estimation rather than mathematical calculations. It is often used in situations where exact probabilities are difficult to determine, relying on an individual's experience or belief about the likelihood of an event.
Examples & Analogies
For instance, if a weather forecaster says there is a 70% chance of rain tomorrow, this is a subjective probability based on their expertise, experience, and understanding of weather patterns. They aren’t calculating outcomes like in classical or empirical methods but rather estimating based on their knowledge.
Properties of Probability
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Bounds: 0 ≤ P(E) ≤ 1
• Complement Rule: \( P(E') = 1 - P(E) \), where E' is the event "not E".
• Certain & Impossible Events: P(S) = 1 and P(∅) = 0.
• Addition Rule: For two events A, B:
\[
P(A \cup B) = P(A) + P(B) - P(A \cap B)
\]
If disjoint, \( P(A \cap B) = 0 \) → \( P(A \cup B) = P(A) + P(B) \).
Detailed Explanation
There are fundamental properties that define how probability functions operate. First, the probability of an event lies between 0 (impossible) and 1 (certain). The complement rule allows us to find the probability of an event not occurring. For certain events, the probability of the sample space, P(S), is always 1, while the probability of the empty set, P(∅), is 0. The addition rule enables us to calculate the probability of either of two events occurring, adjusting for any overlap between them.
Examples & Analogies
Think of rolling a die: the probability of rolling a number greater than 1 (event A) and the probability of rolling an even number (event B). If both events can happen at the same time, we would calculate their combined probability using the addition rule, ensuring we don’t double count any overlapping outcomes.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Classical Probability: Derived from equally likely outcomes using a straightforward formula.
-
Empirical Probability: Based on experimental results rather than theoretically calculated chances.
-
Subjective Probability: Personal estimation of likelihood based on experience.
-
Complement Rule: A method to find the probability of an event not occurring.
-
Addition Rule: A way to combine probabilities of two or more events.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Rolling a die to find the probability of getting a 5, calculated as 1 favorable outcome over 6 total outcomes.
-
Conducting an experiment where a coin is flipped 50 times with heads resulting 30 times, yielding an empirical probability of 0.6 for heads.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Probability's a fine decree, favorable over total is the key!
📖 Fascinating Stories
-
Imagine rolling dice in a game, the chance of a 6 is part of the fame. Count the sides, six are there, one is needed to win, fair!
🧠 Other Memory Gems
-
Remember 'E for Empirical', it’s observed, while 'C for Classical', outcomes are conserved.
🎯 Super Acronyms
Think of 'CEP' - Classical, Empirical, and Subjective - the three types of probability.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Probability
Definition:
A numerical measure of how likely an event is to occur, ranging from 0 (impossible) to 1 (certain).
-
Term: Classical Probability
Definition:
Probability calculated under the assumption that all outcomes are equally likely.
-
Term: Empirical Probability
Definition:
Probability calculated based on observed results from experiments.
-
Term: Subjective Probability
Definition:
Probability derived from personal judgment rather than strict calculation.
-
Term: Sample Space (S)
Definition:
The set of all possible outcomes of an experiment.
-
Term: Event
Definition:
A subset of the sample space; a specific outcome or set of outcomes.