Enrol to start learning
Reading is open to everyone. Enrolling is free, and it is what unlocks the audio lessons, practice tests and progress tracking.
1. What is a Linear Inequality?
Interactive Audio Lesson
Unlock the classroom podcast
The transcript is above and free to read. A free account plays the conversation back.
Create a free account
Today, we will explore what linear inequalities are. Can anyone tell me how linear inequalities differ from linear equations?
I think equations show a specific value, while inequalities show a range of values.
Exactly, well done! Linear inequalities use symbols such as < and > to compare values. Can anyone give me an example?
Like 2x - 3 < 5?
Great example, Student_2! Remember, inequalities are crucial in understanding constraints in real-life situations. Think about speed limits or budgets!
So, inequalities help us understand limits?
Yes, they help represent limits and ranges visually. Let's keep this in mind as we dive deeper into how to solve them.
Unlock the classroom podcast
The transcript is above and free to read. A free account plays the conversation back.
Create a free account
Now that we understand the basics, let's look at the standard forms of linear inequalities. In one variable, we use expressions like ax + b < 0. Can anyone identify a similar example?
Maybe something like 3x + 5 ≤ 10?
Perfect, Student_4! And what about in two variables?
It could be something like x + y > 3?
Exactly! Remember, these forms help us set up problems and visualize solutions later. Can someone summarize the difference between the one-variable and two-variable forms?
One variable focuses on a straight line, while two variables create a region on a graph!
Great recall, Student_2! This foundation is key to solving inequalities effectively.
Unlock the classroom podcast
The transcript is above and free to read. A free account plays the conversation back.
Create a free accountLet's move on to solving linear inequalities. What's the first step in solving 2x - 3 < 5?
I think we would add 3 on both sides to start.
Correct! And after simplifying to 2x < 8, what would we do next?
Dividing by 2 to get x < 4!
Absolutely! When we have to multiply or divide by a negative, remember to reverse the sign. Why is that important?
Because it changes the direction of the inequality!
Yes! This rule avoids confusion and is essential for correct solutions. Let’s visualize some inequalities on a number line.
Unlock the classroom podcast
The transcript is above and free to read. A free account plays the conversation back.
Create a free accountWhen graphing inequalities, how do we decide between an open or closed circle?
Open circles are for < and >, and closed circles are for ≤ and ≥!
Exactly! And shading indicates the range of solutions. If we have x < 3, which way do we shade?
To the left, because it includes all numbers less than 3.
Well put, Student_3! Remember, our goal is to visualize the inequality solutions effectively.
Reference YouTube Videos
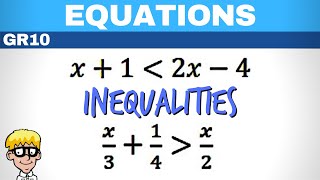
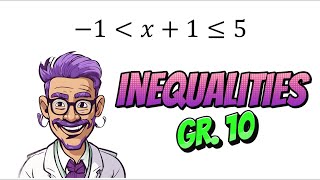
Audio Book
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free accountA linear inequality is similar to a linear equation, but instead of an ‘=’ sign, it uses inequality signs: • < (less than) • ≤ (less than or equal to) • > (greater than) • ≥ (greater than or equal to)
Detailed Explanation
A linear inequality is an expression that represents a relationship between two values where one value is not necessarily equal to the other. Instead of using an equals sign, it employs symbols like <, >, ≤, or ≥. These symbols help us understand whether one side of the inequality is less than, greater than, or equal to the other side, providing a range of possible solutions instead of a single value.
Examples & Analogies
Think of it like a speed limit sign on a road. Instead of saying you must drive at exactly 50 km/h, it might say you must drive 'less than or equal to 50 km/h.' This gives drivers a variety of acceptable speeds, similar to how linear inequalities provide a range of values.
Key Concepts
Core takeaways and short definitions to help you quickly recall the key ideas from this section.
Definition of Linear Inequality: A mathematical expression that uses inequality symbols <, ≤, >, or ≥.
Standard Forms: Inequalities can be expressed in standard forms for one or two variables.
Graphical Representation: Solutions are represented visually on number lines or coordinate planes.
Examples
Memory Aids
Interactive tools to help you remember key concepts