Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Simple Harmonic Motion
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're diving into Simple Harmonic Motion, or SHM. Who can tell me what SHM is?
Isn't it a type of oscillation?
Correct! SHM is a periodic motion where the restoring force is directly proportional to the displacement from equilibrium. Can someone give me the mathematical representation of this principle?
I think it's F equals negative kx, right?
Exactly! We use the equation F = -kx. Here, **F** is the restoring force, **k** is the spring constant, and **x** is the displacement. Letβs remember that negative signβit indicates that the force opposes the direction of displacement. Quite important in understanding SHM!
Acceleration and Energy in SHM
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's talk about acceleration. How is acceleration related to displacement in SHM?
I remember it's a = -ΟΒ²x!
Right! It showcases that acceleration not only depends on displacement but is also directed towards the equilibrium position. Now, letβs grasp how energy is conserved in SHM. What can you tell me about kinetic and potential energy?
Kinetic energy and potential energy transform into each other, but the total energy is constant.
Yes! The kinetic energy is given by KE = Β½mvΒ², and potential energy by PE = Β½kxΒ². Both forms oscillate back and forth while the total remains constant.
Examples of SHM
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs clarify SHM through practical examples! Whatβs one system that follows SHM?
A mass-spring system?
Exactly! The period for a mass on a spring is T = 2Οβ(m/k). What about another system?
Oh, a pendulum!
Correct again! For small angles, a pendulum behaves like SHM with a period T = 2Οβ(l/g). It's fascinating how these principles apply to various systems!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In SHM, the restoring force is directly related to the displacement, leading to oscillatory motion characterized by defined mathematical relationships for force, acceleration, and energy forms. Typically modeled examples include mass-spring systems and pendulums.
Detailed
Simple Harmonic Motion (SHM)
Definition and Characteristics: Simple Harmonic Motion is a periodic motion where the restoring force acting on an object is directly proportional to its displacement from the equilibrium position, directed towards that position. Its mathematical expression is given by the equation:
$$ F = -kx $$
where F is the restoring force, k is the spring constant, and x is the displacement. The acceleration can be described by:
$$ a = -\omega^2 x $$
showing a clear link between displacement and acceleration. The displacement as a function of time is defined as:
$$ x(t) = A \cos(\omega t + \phi) $$
where A is the amplitude and Ο is the phase constant.
Energy in SHM: In this motion, energy oscillates between kinetic and potential forms, yet the total mechanical energy remains constant!
- Kinetic Energy (KE):
$$ KE = \frac{1}{2} m v^2 = \frac{1}{2} m \omega^2 (A^2 - x^2) $$
- Potential Energy (PE):
$$ PE = \frac{1}{2} k x^2 = \frac{1}{2} m \omega^2 x^2 $$
- Total Energy (E):
$$ E = KE + PE = \frac{1}{2} m \omega^2 A^2 $$
Examples of SHM: Two classic cases include:
1. Mass-Spring System: Exhibits oscillation with a period given by:
$$ T = 2\pi \sqrt{\frac{m}{k}} $$
2. Simple Pendulum: For small angles, shows similar SHM behavior with a period of:
$$ T = 2\pi \sqrt{\frac{l}{g}} $$
where l is the pendulum length and g is the acceleration due to gravity.
Youtube Videos
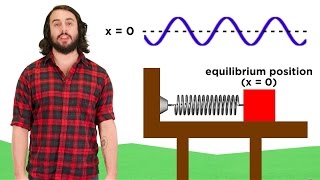
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition and Characteristics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Simple Harmonic Motion (SHM) is a type of periodic motion where the restoring force acting on an object is directly proportional to its displacement from the equilibrium position and is directed towards that position.
Mathematically, this is expressed as:
F = -kx
Where:
β F is the restoring force (N)
β k is the spring constant (N/m)
β x is the displacement from equilibrium (m)
The acceleration a of the object is given by:
a = -ΟΒ²x
Where:
β Ο is the angular frequency (rad/s)
The displacement as a function of time is:
x(t) = A cos(Οt + Ο)
Where:
β A is the amplitude (m)
β Ο is the phase constant (rad)
Detailed Explanation
Simple Harmonic Motion, or SHM, describes a special kind of motion that repeats over time, like a back-and-forth swing of a pendulum. The key idea is that there is a force trying to restore the object back to its starting position, which depends on how far the object is from that position. This relationship is captured in Hooke's Law: F = -kx, where F is the restoring force, k is a constant that measures how stiff a spring is, and x is how far the object has moved from its original position. If you pull back a spring and let go, the force pulls it back to its rest position.
The motion's characteristics are defined mathematically. The acceleration of the object is related to its displacement from the equilibrium position by a factor of angular frequency. The formula a = -ΟΒ²x shows that the acceleration is also directed back towards the equilibrium. Lastly, the position of the object at any given time can be found using x(t) = A cos(Οt + Ο), which shows that the displacement oscillates in a rhythmic pattern, influenced by the amplitude (the maximum distance it moves from the center) and the phase constant.
Examples & Analogies
Think of a swing at a playground. When you push it away from its resting position, it wants to return back, thanks to the gravitational force pulling it down. If you let it go, it swings back and forth. The farther you pull it (greater displacement), the stronger the pull back will be (larger restoring force). The swing follows a predictable path, continuously repeating its motion, just like SHM.
Energy in SHM
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In SHM, energy oscillates between kinetic and potential forms, but the total mechanical energy remains constant (assuming no damping).
β Kinetic Energy (KE):
KE = 1/2 mvΒ² = 1/2 mΟΒ²(AΒ² - xΒ²)
β Potential Energy (PE):
PE = 1/2 kxΒ² = 1/2 mΟΒ²xΒ²
β Total Energy (E):
E = KE + PE = 1/2 mΟΒ²AΒ²
Detailed Explanation
In SHM, energy does not simply disappear; instead, it is transformed back and forth between two forms: kinetic energy (the energy of motion) and potential energy (the stored energy when displaced). At the maximum displacement, the potential energy is highest because the object has been stretched or compressed the most. Conversely, when the object is at its equilibrium position (at rest), its speed is at its highest, resulting in maximum kinetic energy. This interplay maintains a constant total energy throughout the motion, as long as no external forces are acting to 'damp' the motion, such as friction.
The equations KE = 1/2 mvΒ² and PE = 1/2 kxΒ² give us a way to calculate these energy forms using the mass (m), displacement (x), and spring constant (k). The relationship shows how the kinetic energy at a certain point depends upon how far the object is from its rest position and adjusts accordingly as the object moves.
Examples & Analogies
Imagine a child on a swing. At the highest point of the swing, the child has maximum potential energy (like having a ball held high) but minimal kinetic energy (the swing is momentarily still). As the swing moves down towards the lowest point, that potential energy is converted to kinetic energy, making the child swing faster. The total energy (potential + kinetic) remains balanced throughout the swing's motion, illustrating the energy transformation in SHM.
Examples of SHM
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Mass-Spring System: A mass attached to a spring oscillates with a period:
T = 2Οβ(m/k)
β Simple Pendulum: For small angles, a pendulum exhibits SHM with a period:
T = 2Οβ(l/g)
Where:
β l is the length of the pendulum (m)
β g is the acceleration due to gravity (9.81 m/sΒ²)
Detailed Explanation
There are various systems that exemplify Simple Harmonic Motion. One common example is the mass-spring system, where a weight attached to a spring will move back and forth when pulled. The time it takes to complete a full cycle (the period) depends on the mass (m) and how stiff the spring is (k). The formula T = 2Οβ(m/k) helps calculate this period.
Another example is a simple pendulum, where a weight swings at the end of a string. For small angles, the motion is close to SHM, and its period can be calculated with T = 2Οβ(l/g), where l is the length of the string and g is the gravitational pull on the mass. These examples reveal how diverse systems can illustrate the principles of SHM, reinforcing the mathematical relationships that govern their movements.
Examples & Analogies
Consider a swing as an example of a pendulum. The swing's time to go back and forth depends on how long the ropes are. If you pull the swing up slightly and let it go, it will move back and forth, oscillating in a manner similar to the mass-spring system. All these examples from everyday life demonstrate the principles of SHM and make these abstract concepts more accessible.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Restoring Force: The force that acts to return the system to its equilibrium position.
-
Total Energy: The sum of kinetic and potential energy in SHM is constant.
-
Period: The time taken to complete one full oscillation.
-
Energy Transformation: Energy in SHM oscillates between kinetic and potential forms.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A mass-spring system oscillates with a restoring force proportional to displacement.
-
A simple pendulum exhibits SHM for small angles with a predictable period.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Restoring force like a spring, back to equilibrium it brings.
π Fascinating Stories
-
Imagine a swing at the park. It goes forward (max height) and backward (equilibrium) continuously, showcasing the rhythm of SHM.
π§ Other Memory Gems
-
Remember 'RAP' for SHM: Restoring force, Amplitude, Period.
π― Super Acronyms
SHM
- Swaying Happily in Motion!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Simple Harmonic Motion (SHM)
Definition:
A type of periodic motion where the restoring force is proportional to the displacement from equilibrium.
-
Term: Restoring Force
Definition:
The force that acts to bring a system back to its equilibrium position.
-
Term: Amplitude (A)
Definition:
The maximum displacement from the equilibrium position.
-
Term: Spring Constant (k)
Definition:
A measure of the stiffness of a spring, defined as the force required to compress or extend the spring per unit distance.
-
Term: Angular Frequency (Ο)
Definition:
The rate of oscillation; related to the frequency of the motion.
-
Term: Kinetic Energy (KE)
Definition:
The energy of an object due to its motion.
-
Term: Potential Energy (PE)
Definition:
The energy stored in an object due to its position or configuration.
-
Term: Period (T)
Definition:
The time taken to complete one full cycle of the motion.
-
Term: Frequency (f)
Definition:
The number of oscillations occurring in a unit of time.