Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Gravitational Force
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're going to discuss gravitational force and how it affects two masses. Can anyone tell me about Newton's Law of Universal Gravitation?
Isn't it the law that says every mass attracts every other mass?
Exactly! This attraction can be quantified by the formula F = G(mβmβ/rΒ²). What do the symbols represent?
F is the gravitational force, right? And G is the gravitational constant?
Correct! And what can you tell me about mβ, mβ, and r?
mβ and mβ are the masses, and r is the distance between them.
Great! Remember, this law helps us to understand how gravity works in our universe.
So, it means that the farther apart two masses are, the lesser the force between them?
Exactly! This is critical for understanding everything from our actions on Earth to the movements of stars in the galaxy. Let's move on to gravitational field strength.
Gravitational Field Strength
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let's talk about gravitational field strength. Can anyone tell me how we define gravitational field strength?
Is it the force experienced by a mass in the gravitational field?
Yes! It's actually the force per unit mass. The formula is g = F/m = GM/rΒ². Who can break this down for us?
So, G is the gravitational constant, M is the mass creating the field, and r is how far away we are from that mass?
Exactly! And as you get closer to the mass, g increases. Can anyone give an example of where this applies?
Like how gravity is stronger on the surface of the Earth compared to when you're in space!
Great example! Letβs summarize: gravitational field strength tells us how strong the gravitational pull is at a certain distance from a mass. Now, letβs explore gravitational potential.
Gravitational Potential
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Who remembers what gravitational potential is?
It's the work done to bring a mass from infinity to a point in a gravity field.
Right! And the equation is V = -GM/r. Why is it always negative?
Because you have to do work against the gravitational field to move a mass away?
Exactly! Thatβs an important point to remember. Can anyone think of a practical example of gravitational potential?
When launching rockets, they have to overcome this gravitational potential to reach space!
Perfect! Gravitational potential plays a big role in space exploration.
Equipotential Surfaces
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's discuss equipotential surfaces. Who can explain what they are?
Theyβre areas where gravitational potential is constant, meaning no work is needed to move objects along them!
Well put! Why does this matter?
Because it simplifies things when analyzing movements in a gravitational field?
Exactly! If youβre on an equipotential surface, the potential energy doesnβt change. What's a real-world application of this concept?
Water flowing down a slope, where the elevation remains constant at horizontal levels.
Great example! Always remember, equipotential surfaces reduce work in gravitational scenarios. Now, letβs wrap up!
Escape Velocity
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Can anyone tell me what escape velocity means?
It's the speed needed to break free from a gravitational field without propulsion.
Exactly! The formula is v_escape = β(2GM/r). What do G, M, and r represent?
G is the gravitational constant, M is the mass of the body, and r is the distance from its center.
Perfect! Why do we need to achieve this speed?
To escape the gravitational pull and go into space!
Exactly! This is crucial for understanding space missions, like launching rockets. Let's summarize.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section discusses gravitational fields, focusing on the fundamental force of gravity as articulated by Newton's Law of Universal Gravitation. It elaborates on gravitational field strength, gravitational potential, equipotential surfaces, and the concept of escape velocity, establishing how these principles describe the influence of mass on objects in space.
Detailed
Gravitational Fields
Gravitational fields are crucial in understanding the forces that govern the attraction between massive bodies. Newton's Law of Universal Gravitation states that every mass attracts every other mass with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between their centers. The formula is given by:
F = G(mβmβ/rΒ²)
Here, F represents gravitational force, G is the gravitational constant (6.674Γ10β»ΒΉΒΉ NmΒ²/kgΒ²), mβ and mβ are the masses, and r is the distance between their centers.
The gravitational field strength (g) at a point is defined as the gravitational force experienced per unit mass at that point, represented as:
g = F/m = GM/rΒ²
Where M is the mass creating the field, and varies with distance.
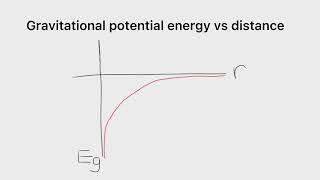
Gravitational potential (V) is the work done per unit mass to bring a mass from infinity to a point in a gravitational field, expressed as:
V = -GM/r
This potential is always negative, indicating that work must be performed against the field to move a mass outward. Equipotential surfaces are areas where the gravitational potential remains constant, meaning no work is needed to move a mass along these surfaces. The escape velocity is the minimum speed required to break free from a celestial body's gravitational influence without additional propulsion, calculated using:
v_escape = β(2GM/r)
Overall, these concepts illustrate how gravitational fields operate and the essential role they play in astrophysics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Gravitational Force
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Gravitational force is the attractive force between two masses. Newton's Law of Universal Gravitation quantifies this force:
F=G\frac{m_1 m_2}{r^2}
Where:
β F is the gravitational force between two masses,
β G is the gravitational constant (6.674Γ10β11 NmΒ²/kgΒ²),
β m1 and m2 are the masses, and
β r is the distance between the centers of the two masses.
Detailed Explanation
Gravitational force is the pull that two masses exert on each other. It's calculated using Newton's Law of Universal Gravitation, which states that the force (F) is equal to the gravitational constant (G) multiplied by the product of the two masses (m1 and m2) divided by the square of the distance (r) between them. This law implies that the greater the mass of an object, the stronger the gravitational force it exerts, and the further apart two objects are, the weaker the gravitational force between them becomes.
Examples & Analogies
Imagine two balloons filled with air. If they are close together, they have a stronger pull on each other just like two massive objects do. But if you move them farther apart, the attraction decreases, similar to how gravitational force operates.
Gravitational Field Strength
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The gravitational field strength (g) at a point in space is the force per unit mass experienced by a small test mass placed at that point:
g=\frac{F}{m} = \frac{GM}{r^2}
Where:
β M is the mass creating the gravitational field, and
β r is the distance from the mass to the point in question.
Detailed Explanation
Gravitational field strength describes how strong the gravitational influence is at a certain point in space. It tells us how much force (F) a unit mass (m) would feel due to the presence of a mass (M) at a distance (r). The formula shows that gravitational field strength increases as the mass creating the field increases or as the distance decreases.
Examples & Analogies
Think of being in a park. Near the base of a tall slide (which acts like a large mass), you feel a strong pull towards it (like gravity). But if you were higher up on a hill (moving away, r gets larger), you'd feel less pull, just as you would if you were farther from a planet.
Gravitational Potential
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Gravitational potential (V) at a point is the work done per unit mass to bring a small test mass from infinity to that point:
V = -\frac{GM}{r}
Gravitational potential is always negative, indicating that work must be done against the gravitational field to move a mass away from the source.
Detailed Explanation
Gravitational potential measures how much work would be needed to move a mass from far away (infinity) to a specific point in a gravitational field. The noticeable aspect of gravitational potential is that it's always negative, indicating that moving away from a mass in a gravitational field requires energy because of the attractive nature of gravity.
Examples & Analogies
Consider a heavy backpack. If youβre standing at the top of a hill (a point of high gravitational potential), you would need to exert energy (work) to lift it off the ground and move it to the top. If you want to drop it back down (moving toward the mass), gravity helps pull it down, indicating that moving away requires effort while moving closer does not.
Equipotential Surfaces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Equipotential surfaces are regions where the gravitational potential is constant. Moving a mass along an equipotential surface requires no work, as there is no change in potential energy.
Detailed Explanation
Equipotential surfaces are areas where the gravitational potential remains the same, meaning there is no change in potential energy when moving within that surface. Because the potential does not change, no work is needed to move a mass along this surface. This principle is crucial for understanding energy conservation in gravitational fields.
Examples & Analogies
Imagine walking on a flat hilltop (an equipotential surface). No matter where you walk on this flat area, you are at the same height (and thus the same gravitational potential), so you donβt need to exert upward or downward force. On a slope, however, youβd need energy to climb, just as you would if you were moving between different gravitational potentials.
Escape Velocity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Escape velocity is the minimum speed needed for an object to escape the gravitational influence of a massive body without further propulsion:
vescape = \sqrt{\frac{2GM}{r}}
Where:
β M is the mass of the celestial body, and
β r is the distance from the center of the mass to the point of escape.
Detailed Explanation
Escape velocity is the speed needed for an object to break free from the gravitational pull of a planet or other massive body without using any propulsion systems after its initial launch. This speed is derived from gravitational forces and depends on the mass of the body being escaped from and the distance from its center. The larger the mass or the closer the object is, the higher the escape velocity needed.
Examples & Analogies
Think of a ball thrown into the air. If you only throw it gently, it will fall back due to Earth's gravity. However, if you throw it hard enough (think of how a rocket launches), it can reach a point where the force of gravity is no longer strong enough to pull it back downβthis point is achieved at escape velocity.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Gravitational Force: The force attracting two masses, defined by the equation F = G(mβmβ/rΒ²).
-
Gravitational Field Strength: Defined as g = F/m, indicating the force experienced per unit mass in a gravitational field.
-
Gravitational Potential: Expressed as V = -GM/r, represents work done per unit mass to move from infinity.
-
Equipotential Surfaces: Areas of constant gravitational potential where no work is needed to move within them.
-
Escape Velocity: The minimum speed to escape a gravitational field, calculated by v_escape = β(2GM/r).
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The gravitational force between the Earth and an apple causes it to fall to the ground.
-
A satellite in orbit experiences a specific gravitational field strength due to Earth's mass.
-
The gravitational potential on a mountain is higher than at sea level due to work done against gravity.
-
The Moon orbits Earth along an equipotential surface as it maintains constant gravitational potential.
-
A rocket must reach escape velocity to break free from Earth's gravity and enter space.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Gravity pulls objects near, stronger when theyβre close and clear.
π Fascinating Stories
-
Imagine climbing a mountain, the higher you go, the harder it is to pull away from the ground, just like in space with gravity!
π§ Other Memory Gems
-
GPE - Gravitational Potential Energy: Great People Escape, symbolizing escaping gravity takes energy.
π― Super Acronyms
G's Favors - GFS - Gravitational Force, Field Strength, and Escape Velocity.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Gravitational Force
Definition:
The attractive force between two masses, quantified by Newton's Law of Universal Gravitation.
-
Term: Gravitational Field Strength
Definition:
The force per unit mass experienced by a small mass placed in a gravitational field.
-
Term: Gravitational Potential
Definition:
The work done per unit mass to move a mass from infinity to a point in a gravitational field.
-
Term: Equipotential Surfaces
Definition:
Surfaces where gravitational potential is constant, requiring no work to move a mass along them.
-
Term: Escape Velocity
Definition:
The minimum speed needed for an object to escape a gravitational field without additional propulsion.