Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Interior Angles of Polygons
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will learn about the angles in polygons. Let's start with triangles. Who can tell me the sum of the interior angles in a triangle?
Is it 180 degrees?
That's right! The formula we use is simply 'Sum = 180 degrees'. Now, how about quadrilaterals? What do you think the sum of the interior angles is?
I think it's 360 degrees.
Exactly! The formula is 'Sum = 360 degrees'. Now, who can explain how we find the sum of a polygon with 'n' sides?
We use the formula (n - 2) times 180 degrees!
Excellent! This works because we can divide any polygon into triangles. Remember the acronym 'T-SUM' (Triangle: 180, Sum = n-2), which will help you remember this formula.
Regular Polygons
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now letโs discuss regular polygons. What do we mean by a regular polygon?
It means all sides and angles are equal!
Correct! To find each interior angle of a regular polygon with 'n' sides, we use the formula: Each Interior Angle = ((n - 2) * 180) / n. Can anyone tell me the interior angle of a regular pentagon with 5 sides?
So, it would be ((5 - 2) * 180) / 5, which is 108 degrees?
Exactly! Awesome job! Remember: 'PENT' for Pentagon helps you link 5 sides to the 5 in the formula.
Exterior Angles of Polygons
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letโs move on to exterior angles. What is the sum of the exterior angles of any convex polygon?
Is it always 360 degrees?
That's absolutely correct! No matter how many sides there are, the sum is always 360 degrees. This is important when we're working with real-world shapes like buildings.
Can we use this in practical situations?
Definitely! It's used in architecture, navigation, and many areas where geometry is applied. Remember, 'EX' for exterior angles is all about the extra 360!
So we could design something using these principles?
Absolutely, great connection! Letโs summarize what we've learned: we covered the interior angles of triangles and quadrilaterals, learned the sum of angles in polygons, and touched on regular and exterior angles. Well done, everyone!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section covers the fundamental concepts concerning angles in polygons, detailing how to calculate the sum of interior and exterior angles as well as the specific properties of different types of polygons such as triangles, quadrilaterals, and regular polygons.
Detailed
Angles in Polygons
Understanding angles in polygons is crucial for grasping the broader concepts of geometry. A polygon is defined as a closed two-dimensional shape with straight sides. The section specifically focuses on the following:
1. Sum of Interior Angles of Polygons
- Triangles (3 sides): The sum of the interior angles is always 180 degrees.
- Formula: Sum = 180 degrees.
- Quadrilaterals (4 sides): The sum is always 360 degrees.
- Formula: Sum = 360 degrees.
- General Polygon (n sides): The sum can be calculated using the formula:
- Formula: Sum of Interior Angles = (n - 2) * 180 degrees.
- This means that any polygon can be divided into triangles, where each triangle contributes 180 degrees to the total sum.
2. Regular Polygons
A regular polygon has all sides and angles equal. The measure of each interior angle can be calculated as:
- Formula: Each Interior Angle = ((n - 2) * 180) / n.
3. Sum of Exterior Angles of Polygons
Regardless of the number of sides, the sum of the exterior angles of any convex polygon is always 360 degrees. This can be very useful when determining angle measures while working with polygons in practical applications.
Understanding these principles helps in solving problems related to angles and provides a foundational knowledge necessary for further studies in geometry.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Sum of Interior Angles of Polygons
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
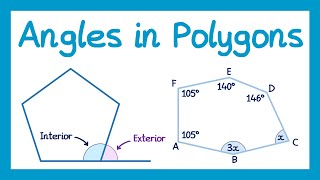
The interior angles are the angles inside the polygon at its vertices.
โ Triangle (3 sides): The sum of the interior angles of any triangle is always 180 degrees.
- Formula: Sum = 180 degrees.
- Example: If a triangle has angles of 70 degrees and 50 degrees, the third angle is 180 - 70 - 50 = 60 degrees.
โ Quadrilateral (4 sides): The sum of the interior angles of any quadrilateral is always 360 degrees.
- Formula: Sum = 360 degrees.
- Example: If a quadrilateral has angles of 80, 90, and 100 degrees, the fourth angle is 360 - 80 - 90 - 100 = 90 degrees.
โ General Polygon (n sides): The sum of the interior angles of a polygon with 'n' sides can be found using the formula:
- Formula: Sum of Interior Angles = (n - 2) * 180 degrees
- Explanation: Any polygon can be divided into (n - 2) triangles by drawing diagonals from one vertex. Since each triangle's angles sum to 180 degrees, this formula holds.
- Example (Pentagon, 5 sides): Sum = (5 - 2) * 180 = 3 * 180 = 540 degrees.
- Example (Hexagon, 6 sides): Sum = (6 - 2) * 180 = 4 * 180 = 720 degrees.
โ Regular Polygons: A polygon is regular if all its sides are equal in length and all its interior angles are equal.
- To find the measure of each interior angle of a regular polygon with 'n' sides:
- Formula: Each Interior Angle = ( (n - 2) * 180 ) / n
- Example (Regular Hexagon): Each Interior Angle = ( (6 - 2) * 180 ) / 6 = (4 * 180) / 6 = 720 / 6 = 120 degrees.
Detailed Explanation
In this chunk, we learn about the sum of the interior angles in polygons. First, we look at specific types of polygons like triangles and quadrilaterals. For a triangle, regardless of its shape, the interior angles will always add up to 180 degrees. So if you know two angles, you can always calculate the third.
Next, for quadrilaterals (four-sided shapes), the total interior angles add up to 360 degrees, which means if you know three angles, you can easily calculate the fourth.
For polygons with more than four sides, there's a formula we can use: the sum of the interior angles is equal to (number of sides - 2) times 180 degrees. For example, a pentagon has 5 sides. Using the formula, we find the sum of its interior angles is (5 - 2) * 180 = 540 degrees.
Lastly, we define regular polygons, where all sides and interior angles are equal. The formula to find each interior angle of a regular polygon is the total sum of angles divided by the number of angles. For instance, in a regular hexagon, the total sum of angles is 720 degrees, so each angle is 720 / 6 = 120 degrees.
Examples & Analogies
Imagine you're designing a new playground. The design includes a triangular sandbox, which needs to have its sides measured correctly to ensure all parts fit together without any gaps. Knowing that the angles inside this triangle must always sum up to 180 degrees helps you determine the angles when planning the structure. If you design a larger play area shaped like a pentagon, understanding that its angles add up to 540 degrees ensures all components of the structure are accurately aligned.
Sum of Exterior Angles of Polygons
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The exterior angles of a polygon are formed by extending one side of the polygon and measuring the angle between the extended side and the adjacent side.
โ The sum of the exterior angles of any convex polygon (regular or irregular) is always 360 degrees.
- Formula: Sum of Exterior Angles = 360 degrees
โ For Regular Polygons: To find the measure of each exterior angle of a regular polygon with 'n' sides:
- Formula: Each Exterior Angle = 360 / n
- Example (Regular Hexagon): Each Exterior Angle = 360 / 6 = 60 degrees.
โ Relationship between Interior and Exterior Angles: An interior angle and its adjacent exterior angle always form a straight line, so they sum to 180 degrees.
- Formula: Interior Angle + Exterior Angle = 180 degrees.
- Example: For a regular hexagon, Interior Angle = 120 degrees, Exterior Angle = 60 degrees. 120+60=180.
Detailed Explanation
In this section, we're discussing the exterior angles of polygons. An exterior angle is made when you extend one side of a polygon and measure the angle formed with the adjacent side. A key property of exterior angles is that, regardless of the number of sides a polygon has, if you add up all the exterior angles, they'll always sum up to 360 degrees.
For regular polygons, where all angles are equal, you can find each exterior angle by dividing 360 degrees by the number of sides. For example, in a regular hexagon (6 sides), each exterior angle measures 360 / 6 = 60 degrees.
Additionally, there's an important relationship between interior and exterior angles of a polygon. They always add up to 180 degrees, meaning if you know one, you can find the other.
Examples & Analogies
Think of a stop sign, which is an octagon (8 sides). When you're at the stop sign, each corner (or vertex) represents the end of one exterior angle as you turn your car to face the next side. If you were to measure all the angles outside that octagon, they would sum to 360 degrees, showing how smoothly your car can transition around the sign. Understanding these angles helps traffic designers create safer and more efficient roadways.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Interior Angles: The sum of interior angles in a triangle is 180 degrees, whereas in quadrilaterals it is 360 degrees.
-
Regular Polygons: Regular polygons have equal sides and angles; the measure of each angle can be calculated using the specific formula.
-
Exterior Angles: The sum of exterior angles for any polygon is 360 degrees.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a triangle with angles of 70 and 50 degrees, the third angle can be calculated as 180 - 70 - 50 = 60 degrees.
-
In a quadrilateral with angles of 80, 90, and 100 degrees, the fourth angle can be determined using 360 - 80 - 90 - 100 = 90 degrees.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
๐ต Rhymes Time
-
A triangle's angles add to hundred and eighty, quadrilaterals add up to three sixty, that's a fact, it's never shady.
๐ Fascinating Stories
-
Imagine a polygon party where every angle knows how much room it has. The triangle feels light at 180, the quadrilateral brings the total to 360, making it a grand affair for shapes!
๐ง Other Memory Gems
-
T for Triangle = 180, Q for Quadrilateral = 360. TQ (T and Q) is a quick way to remember angle sums.
๐ฏ Super Acronyms
Remember 'I for Interior and E for Exterior' both add up to 360 for exterior angles.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Polygon
Definition:
A closed two-dimensional shape with straight sides.
-
Term: Interior Angles
Definition:
Angles inside a polygon at its vertices.
-
Term: Exterior Angles
Definition:
Angles formed between an extended side of a polygon and an adjacent side.
-
Term: Regular Polygon
Definition:
A polygon with all sides and all angles equal.