Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Perimeter
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we'll begin by understanding what perimeter is. Can anyone tell me what perimeter refers to?
It's how far it is around a shape.
Exactly! Perimeter is the total distance around a 2D shape. For a square, how do we calculate it?
We multiply the side length by 4.
Great job! The formula is Perimeter = 4 * s. Now, how would we find the perimeter of a rectangle?
We add the length and width, then multiply by 2.
Correct! The formula is Perimeter = 2 * (l + w). Letโs remember: โLegoโ for **Length + Width** that makes a rectangle's perimeter. What do you think?
Thatโs a good reminder!
Let's wrap up. Can anyone summarize the perimeter formulas we learned today?
For a square, it's 4 * s, and for a rectangle, it's 2 * (l + w).
Perfect! Understanding perimeter helps in so many real-world contexts.
Exploring Area
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we have covered perimeter, letโs explore area. What does area represent?
It shows how much space is contained within a shape.
Spot on! For a square, what's the area formula?
Area = s squared.
Exactly! Area = sยฒ for squares. And for rectangles?
Area = length times width!
Correct! Remember, **L*W = Area!** Now, how do we find the area of a triangle, do you remember?
It's (1/2) * base * height.
Well done! Let's summarize: square area is sยฒ, rectangle is l*w, and triangle is (1/2) * b * h.
Understanding Circles
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Next, letโs dive into circles! Who can tell me about the radius and diameter?
The radius is from the center to the edge, and the diameter is twice the radius.
Right! Remember: **R to D, twice as far.** Can someone now explain how we find the circumference?
Circumference = ฯ * d!
Good! Or you can also use 2 * ฯ * r. How about the area?
Area = ฯ * r squared.
Exactly! To remember, we can say: **The area of circles goes square, as radius goes round and round.** Well done, everyone!
Compound Shapes
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let's look at compound shapes! Who can explain what a compound shape is?
It's made of two or more simple shapes!
Good! To find the area, we can break it down into simpler parts. Can someone give me an example?
Like a rectangle with a semicircle on top.
Yes! So how would we calculate its area?
We find the area of the rectangle and the semicircle and then add them.
Correct! And what about perimeter?
Add the outside lengths only! Not the inside parts.
Exactly! Great summarization of concepts today!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the definitions and formulas associated with area and perimeter for basic shapes such as squares, rectangles, triangles, parallelograms, trapezoids, and circles. Understanding these concepts is essential for practical applications in real life.
Detailed
Area and Perimeter: Measuring 2D Shapes
In geometry, two essential measurements for two-dimensional figures are area and perimeter. Perimeter is defined as the total distance around the outside of a shape, calculated by summing the lengths of all its sides. Area, on the other hand, refers to the amount of space a shape covers, measured in square units. These measurements are crucial in various real-world applications, from architecture to agriculture.
4.1 Basic 2D Shapes Review
- Square: With a side length 's', the formulas are:
- Perimeter = 4 * s
- Area = sยฒ
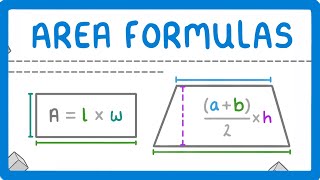
- Rectangle: Given length 'l' and width 'w':
- Perimeter = 2 * (l + w)
- Area = l * w
- Triangle: For base 'b' and height 'h':
- Perimeter = sum of all three sides
- Area = (1/2) * b * h
- Parallelogram: Using base 'b' and perpendicular height 'h':
- Perimeter = 2 * (b + side length)
- Area = b * h
- Trapezoid: For bases 'a' and 'b' and height 'h':
- Perimeter = a + b + side 1 + side 2
- Area = (1/2) * (a + b) * h
4.2 Circles
- Circle: The radius 'r' is the distance from the center to a point on the circle, while the diameter 'd' is double the radius (d = 2r). The circumference, or perimeter of a circle, can be calculated using:
- Circumference = ฯ * d or Circumference = 2 * ฯ * r
- Area = ฯ * rยฒ
4.3 Sectors of Circles
A sector is a 'slice' of the circle formed by two radii and an arc, similar to pizza slices. The arc length and area of a sector can be calculated using:
- Arc Length = (Angle of Sector / 360) * (2 * ฯ * r)
- Area of Sector = (Angle of Sector / 360) * (ฯ * rยฒ)
4.4 Area and Perimeter of Compound Shapes
Compound shapes can be decomposed into simpler shapes to calculate their area and perimeter. Methods include decomposition (adding the areas) and subtraction (finding the area of a larger shape minus parts cut out).
Understanding these concepts equips students with foundational skills essential for practical applications in problem-solving and real-world design.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Area and Perimeter
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Perimeter is the total distance around the outside of a two-dimensional shape. It is a measure of length. Area is the amount of surface a two-dimensional shape covers. It is measured in square units.
Detailed Explanation
Perimeter and area are two fundamental concepts in geometry that measure different properties of two-dimensional shapes. The perimeter is like a fence that goes all the way around a shape, giving us the total length of the sides. For example, if you have a square with each side measuring 4 cm, the perimeter would be 4 cm + 4 cm + 4 cm + 4 cm, which equals 16 cm. Area, on the other hand, measures how much space is inside the shape. For the same square, the area would be 4 cm multiplied by 4 cm, which equals 16 cmยฒ. Thus, perimeter deals with boundary length, while area deals with the space that the shape occupies.
Examples & Analogies
Imagine you are laying out a garden. The perimeter would tell you how much fencing you need to put around the garden to keep out rabbits, while the area would tell you how much soil you need to fill the bed to plant your flowers.
Basic 2D Shapes Review
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Square: Side length 's'
- Perimeter = 4 * s
- Area = s * s = s^2
Rectangle: Length 'l', Width 'w'
- Perimeter = 2 * (l + w)
- Area = l * w
Triangle: Base 'b', Height 'h'
- Perimeter = sum of all three side lengths.
- Area = (1/2) * b * h
Parallelogram: Base 'b', Perpendicular height 'h', Side 's'
- Perimeter = 2 * (b + s)
- Area = b * h
Trapezoid (Trapezium): Parallel sides 'a' and 'b', Height 'h', Non-parallel sides 'c' and 'd'
- Perimeter = a + b + c + d
- Area = (1/2) * (a + b) * h
Detailed Explanation
In this chunk, we review the formulas for calculating the perimeter and area of various two-dimensional shapes. For a square, both the perimeter and area are directly derived from the length of a side 's'. For a rectangle, the perimeter is found by adding up all sides, while the area comes from multiplying length by width. Triangles differ because their perimeter is the sum of all sides, while area uses the base and height to find the space within. Parallelograms and trapezoids follow similar principles but have their specific calculations based on their dimensions. Mastering these formulas allows students to solve geometric problems related to these common shapes.
Examples & Analogies
Think about different rooms in a house. The square room might be a small bedroom, where calculating area helps decide how much carpet you'll need. The rectangle could be the living room; when planning, you need the perimeter to understand how much wallpaper you'll buy if you're covering the walls.
Circle Measurements
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Circles
- Radius (r): Distance from the center to any point on the circle.
- Diameter (d): Distance across the circle through the center (d=2r).
- Pi (pi): A mathematical constant, approximately 3.14159...
Circumference (Perimeter of a Circle):
- Formula: Circumference = pi * d
- Formula: Circumference = 2 * pi * r
- Example: A circle with radius 7 cm. Circumference = 2 * pi * 7 = 14 * pi cm (approx 43.98 cm).
Area of a Circle:
- Formula: Area = pi * r^2
- Example: A circle with radius 7 cm. Area = pi * 7^2 = 49 * pi cm^2 (approx 153.94 cm^2).
Detailed Explanation
In this segment, we explore the properties of circles. The radius is crucial as it measures the distance from the circle's center to its edge. The diameter, which is twice the radius, informs us of how wide the circle is. With circles, we calculate the circumference, which is the measure around the circle. The formulas for circumference use either the diameter or the radius, both involving the mathematical constant pi. Lastly, we calculate the area of the circle to understand how much space it occupies. An example using a radius of 7 cm illustrates these concepts with concrete numbers.
Examples & Analogies
Imagine you have a round pizza. To know how much topping to put on the pizza's edge, you'd calculate the circumference. To find out how much cheese or sauce to spread on the whole pizza, you'd calculate the area. Both calculations help you ensure the pizza is perfectly made!
Sectors of Circles
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Sectors of Circles
A sector is a portion of a circle enclosed by two radii and an arc. It's like a "slice" of pizza.
- Arc Length: The length of the curved part of the sector.
- Formula: Arc Length = (Angle of Sector / 360) * (2 * pi * r)
- Example: A sector of a circle with radius 10 cm and a central angle of 90 degrees.
- Arc Length = (90 / 360) * (2 * pi * 10) = (1/4) * (20 * pi) = 5 * pi cm (approx 15.71 cm).
- Area of a Sector:
- Formula: Area of Sector = (Angle of Sector / 360) * (pi * r^2)
- Example: A sector of a circle with radius 10 cm and a central angle of 90 degrees.
- Area of Sector = (90 / 360) * (pi * 10^2) = (1/4) * (100 * pi) = 25 * pi cm^2 (approx 78.54 cm^2).
Detailed Explanation
Sectors are specific parts of circles, often compared to slices of pizza. Understanding sectors involves learning how to find the arc length and the area of the sector. The arc length formula shows how we calculate the length of the curved edge based on the central angle of the sector. The area of a sector helps us understand how much space the sector takes up within the circle. Both are essential for applications in real-world scenarios where circular segments are involved.
Examples & Analogies
When making a pizza, if you want to know how long the crust (the outer edge of the slice) is, you would calculate the arc length. If you're hosting guests and need to figure out how much pizza you have in total per slice, you'd calculate the area of each slice. This helps you gauge how many slices to cut!
Area and Perimeter of Compound Shapes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Area and Perimeter of Compound Shapes
Compound shapes are formed by combining two or more basic geometric shapes. To find their area or perimeter, you often break them down into simpler components.
- Area of Compound Shapes:
- Method 1 (Decomposition): Divide the compound shape into simpler, non-overlapping shapes (rectangles, triangles, circles/sectors). Calculate the area of each component and add them together.
- Method 2 (Subtraction): Enclose the compound shape within a larger, simple shape (e.g., a rectangle). Calculate the area of the larger shape, then subtract the areas of any "missing" or "cut-out" parts.
- Example (Area by Decomposition): A shape formed by a rectangle (length 8 cm, width 5 cm) with a semi-circle (radius 4 cm) attached to one of its 8 cm sides.
- Area of rectangle = 8 โ 5 = 40 cmยฒ.
- Area of semi-circle = (1/2) * pi * rยฒ = (1/2) * pi * 4ยฒ = 8 * pi cmยฒ (approx 25.13 cmยฒ).
- Total Area = 40 + 8 * pi โ 65.13 cmยฒ.
- Perimeter of Compound Shapes:
- Carefully identify all the outer boundary lengths of the compound shape. Sum only these lengths. Do not include interior lines that separate the component shapes.
- Example (Perimeter of the above shape):
- Two sides of rectangle = 5 cm + 5 cm = 10 cm.
- One side of rectangle = 8 cm.
- Length of semi-circular arc = (1/2) * Circumference of full circle = 4 * pi cm (approx 12.57 cm). Total Perimeter = 5 + 5 + 8 + 4 * pi โ 30.57 cm.
Detailed Explanation
Compound shapes are made up of two or more basic shapes, which can complicate finding their area and perimeter. We can find the area by decomposing the compound shape into simpler shapes, calculating their areas, and summing those values. Alternatively, we can enclose a complex shape within a larger simple one and use subtraction for the area. For perimeter, it's crucial to focus only on the outer boundaries, ignoring any interior edges. This understanding simplifies the measurement of complex shapes.
Examples & Analogies
Imagine building a treehouse where the platform is a rectangle, and it has a circular part for seating. To figure out how much wood to buy for the flooring (area) and how much railing you need (perimeter), you'll need to consider both parts separately, then combine them to get your final numbers. Itโs like assembling a jigsaw puzzle where every piece plays a role in the final picture!
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Perimeter: The total distance around a shape.
-
Area: The amount of surface covered by a shape.
-
Square: Defined by equal side lengths and calculated area and perimeter formulas.
-
Rectangle: Defined with length and width, using specific formulas for area and perimeter.
-
Circle: Defined by radius and diameter, with unique formulas for area and circumference.
-
Compound Shapes: Composed of basic shapes; area and perimeter calculated by combining simple shapes.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The perimeter of a square with each side of 4 cm is calculated as 4 * 4 = 16 cm.
-
The area of a rectangle with a length of 5 m and a width of 3 m is 5 * 3 = 15 mยฒ.
-
For a circle with a radius of 7 cm, the circumference is calculated as 2 * ฯ * 7 โ 43.98 cm and the area is ฯ * 7ยฒ โ 153.94 cmยฒ.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
๐ต Rhymes Time
-
To find the area, measure wide, multiply together, donโt divide.
๐ Fascinating Stories
-
Imagine a garden shaped like a combination of a rectangle and a circle. You want to plant flowers in the area, which means you must add both shapesโ areas to get the total space for planting.
๐ง Other Memory Gems
-
For area, remember: Length times Width is the bid!
๐ฏ Super Acronyms
Remember **P.A.C.** for shapes - Perimeter + Area Calculation.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Perimeter
Definition:
The total distance around the outside of a two-dimensional shape.
-
Term: Area
Definition:
The amount of surface a two-dimensional shape covers, measured in square units.
-
Term: Square
Definition:
A quadrilateral with equal sides and right angles.
-
Term: Rectangle
Definition:
A quadrilateral with opposite sides that are equal and four right angles.
-
Term: Circle
Definition:
A round shape whose points are equidistant from the center.
-
Term: Sector
Definition:
A portion of a circle formed by two radii and an arc.
-
Term: Compound Shape
Definition:
A shape made up of two or more simple geometric shapes.