Enrol to start learning
Reading is open to everyone. Enrolling is free, and it is what unlocks the audio lessons, practice tests and progress tracking.
7.2. Basic Trigonometric Ratios
Interactive Audio Lesson
Unlock the classroom podcast
The transcript is above and free to read. A free account plays the conversation back.
Create a free account
Today we are going to learn about basic trigonometric ratios. These ratios are crucial for understanding properties of right-angled triangles. Let’s start with sine. Who can tell me what sine is?
Isn't sine the ratio of the opposite side to the hypotenuse?
Exactly! We can remember this with the acronym SOH, which stands for 'Sine = Opposite over Hypotenuse'. Now, what about cosine?
Cosine is the adjacent side divided by the hypotenuse, right? That’s CAH.
Great job! CAH stands for 'Cosine = Adjacent over Hypotenuse'. Let’s move on to tangent. Can anyone tell me the definition of tangent?
Tangent is the opposite side divided by the adjacent side, which we can remember with TOA!
Fantastic! TOA stands for 'Tangent = Opposite over Adjacent'. Remembering these acronyms will help you recall the definitions easily. Does anyone have questions about these ratios?
Unlock the classroom podcast
The transcript is above and free to read. A free account plays the conversation back.
Create a free account
Let’s discuss where we can apply these trigonometric ratios. Who can give me an example of where we might use sine?
We could use sine to calculate the height of a building if we know the angle of elevation from a certain distance!
Exactly! The sine ratio helps us find heights and distances in many practical scenarios. What about cosine?
Cosine can help in navigation, right? Like determining how far away something is when you know the angle and one side.
Yes, precisely! Cosine has many applications in navigation and physics. And tangent?
Tangent can be used to find slopes, like in roads or hills.
Excellent! Recognizing these applications makes it easier to see the relevance of trigonometric ratios in everyday life.
Unlock the classroom podcast
The transcript is above and free to read. A free account plays the conversation back.
Create a free accountNow, let’s practice applying these ratios. If we have a right triangle with one angle θ=30° and we know the opposite side is 4 units, how can we find the hypotenuse?
We can use sine! Since , we can set up the equation: .
Correct! Now, what’s the hypotenuse?
The hypotenuse would be 8 units!
Well done! Practicing these calculations will help you become very skilled in applying trigonometric ratios. Let’s try one more problem involving cosine.
Overview
Short Summary
This section covers the fundamental trigonometric ratios related to right-angled triangles, including sine, cosine, and tangent.
Medium Summary
In this section, we explore the basic trigonometric ratios: sine (sin), cosine (cos), and tangent (tan). These ratios connect the angles and sides of right-angled triangles and are essential for various applications in geometry and trigonometry.
Detailed Summary
Basic Trigonometric Ratios
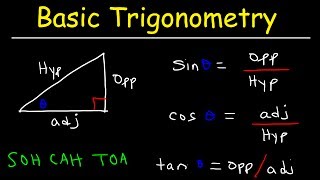
In this section, we focus on the basic trigonometric ratios that are essential for understanding trigonometry, particularly in the context of right-angled triangles. For a given angle θ in a right triangle:
-
Sine (sin) is defined as the ratio of the length of the opposite side to the hypotenuse:
-
Cosine (cos) is defined as the ratio of the length of the adjacent side to the hypotenuse:
-
Tangent (tan) is defined as the ratio of the length of the opposite side to the adjacent side:
These ratios are fundamental in various applications of mathematics, physics, and engineering, helping to solve problems involving angles and distances.
Reference YouTube Videos
Audio Book
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free accountFor a right-angled triangle with an angle θ, the three primary trigonometric ratios are defined as follows:
Detailed Explanation
In trigonometry, we study the properties of right-angled triangles. The three primary ratios, which we refer to as sine, cosine, and tangent, are essential in linking angles to the lengths of triangle sides. Angle θ is one of the angles in the triangle, apart from the right angle. The relationships help us find unknown sides or angles based on known values.
Examples & Analogies
Imagine you are standing at the foot of a ladder leaning against a wall. The angle that the ladder makes with the ground is like angle θ. By knowing the length of the ladder and how high it reaches up the wall, you can understand their relationships using these ratios.
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free account● Sine (sin): sin θ = Opposite side / Hypotenuse
Detailed Explanation
The sine ratio of angle θ is defined as the length of the opposite side divided by the length of the hypotenuse. The opposite side refers to the side that is directly opposite to angle θ, while the hypotenuse is the longest side of the right-angled triangle, opposite the right angle.
Examples & Analogies
Consider a situation where you are measuring the height of a tree. If you know how far you are standing from the tree (the base of the triangle's adjacent side), and the length of the rope you throw high (the hypotenuse), using sine helps you find the height of the tree (the opposite side).
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free account● Cosine (cos): cos θ = Adjacent side / Hypotenuse
Detailed Explanation
The cosine ratio relates the length of the adjacent side to the length of the hypotenuse. The adjacent side is the side that is next to angle θ and is not the hypotenuse. This ratio helps us find out how much of the triangle’s base length correlates with the angle.
Examples & Analogies
Think of a ladder leaning against a wall again. If the wall represents the height of the triangle, then the distance from the wall to the base of the ladder represents the adjacent side. The cosine tells us how the angle of the ladder affects that distance, helping us gauge how steep the ladder is.
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free account● Tangent (tan): tan θ = Opposite side / Adjacent side
Detailed Explanation
The tangent ratio describes the relationship between the length of the opposite side and the adjacent side. This is especially useful in calculating angles from known side lengths, making it a practical tool in various fields like engineering and architecture.
Examples & Analogies
Imagine you're flying a kite. The height of the kite (the opposite side) and the distance you are from the point directly below the kite (the adjacent side) can be in a triangle. When you know these lengths, tangent helps you figure out how high the kite is being flown relative to your position.
--
Key Concepts
Examples
Step-by-step examples to apply the section's ideas and test your understanding.
Example 1: In a right triangle where θ = 30°, if the opposite side is 3 units, then the hypotenuse can be found using sin θ = opposite/hypotenuse, giving hypotenuse = 3/sin(30°) = 6 units.
Example 2: For a right triangle with θ = 45°, if the adjacent side is 5 units, the hypotenuse becomes hypotenuse = 5/cos(45°) = 5√2 units.
Memory Aids
Interactive tools to help you remember key concepts
Stories
Memory Tools
Flash Cards
Glossary
Sine
A trigonometric ratio defined as the ratio of the opposite side to the hypotenuse in a right triangle.
Cosine
A trigonometric ratio defined as the ratio of the adjacent side to the hypotenuse in a right triangle.
Tangent
A trigonometric ratio defined as the ratio of the opposite side to the adjacent side in a right triangle.