Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Tangent and Its Relation to Sine and Cosine
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will discuss the relationship between the tangent function and the sine and cosine functions. Can anyone tell me how we define tangent?
Tangent is the opposite side over the adjacent side.
That’s correct! But there’s an even better way to express this. Tangent can also be written as the ratio of sine to cosine. Can someone recall how this looks?
Oh! It’s \( \tan \theta = \frac{\sin \theta}{\cos \theta} \)
Exactly! This shows how tangent connects sine and cosine. Remember, Sine is like the height, Cosine is like the base, and together, they form the tangent. A good way to remember this is 'Tan is happy between Sin and Cos'.
So, does this mean we always need to know sine and cosine values to find tangent?
Yes! Knowing sine and cosine is crucial to finding tangent. Let’s summarize: Tangent is the ratio of sine to cosine and connects both functions in a unique way.
Exploring Cotangent
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we understand tangent, let's move to cotangent. Can someone explain how cotangent is defined?
Cotangent is the opposite of tangent, right?
You're getting there! Cotangent is actually the ratio of cosine to sine. It can be expressed as: \( \cot \theta = \frac{\cos \theta}{\sin \theta} \).
So, if tangent is \( \frac{\sin \theta}{\cos \theta} \), is cotangent just flipping it?
Exactly! You flipped it just right! This reciprocal nature is a key concept. To help you remember, think of 'Cot is cool, it flips Sine to rule!'.
Is there a way to remember these relationships overall?
Great question! Just remember: Tan 'sticks' with Sin and Cos, while Cot 'flips' but stays linked. It’s all about connection!
Pythagorean Identity
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let’s discuss a very important identity, often covered in trigonometry—\( \sin^2 \theta + \cos^2 \theta = 1 \). What does this identity tell us?
It shows that the sum of the squares of sine and cosine equals one.
Excellent! This relationship is crucial in many trigonometric applications. It's called the Pythagorean identity. Can you think of why it's so important?
It helps in proving other identities or solving for angles, right?
Exactly! It’s the backbone of numerous proofs. For instance, if we need to find the cosine value from sine, we can rearrange this. Remember this key point: 'Sin and Cos are best friends in this identity!'.
So can we use this identity to solve problems?
Absolutely! Understanding this identity allows you to manipulate and discover unknown values in trigonometric equations. To wrap up, remember: 'Pythagorean identity keeps Sine and Cosine mighty!'
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore how tangent and cotangent are derived from sine and cosine, as well as the fundamental identity that relates sine and cosine functions. Understanding these relationships is essential for solving more complex trigonometric problems.
Detailed
Detailed Summary
This section delves into significant relationships among trigonometric ratios, particularly focusing on three fundamental expressions:
-
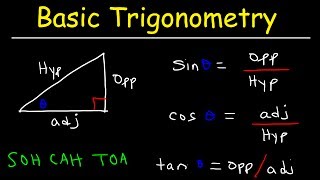
The tangent function, defined as the ratio of sine to cosine:
$$ \tan \theta = \frac{\sin \theta}{\cos \theta} $$
This illustrates how tangent is derived from the primary ratios sine and cosine. -
The cotangent function, defined as the ratio of cosine to sine:
$$ \cot \theta = \frac{\cos \theta}{\sin \theta} $$
This demonstrates the reciprocal nature of the tangent and cotangent functions. -
The Pythagorean identity relating sine and cosine:
$$ \sin^2 \theta + \cos^2 \theta = 1 $$
This identity is fundamental to many trigonometric proofs and applications and helps in establishing various trigonometric transformations and computations.
These established relationships are critical for advanced problem-solving in trigonometry and understanding the behavior of angles and triangles.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Tangent Ratio as Sine over Cosine
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
● tan θ = \( \frac{\sin θ}{\cos θ} \)
Detailed Explanation
The tangent of an angle (θ) can be understood as the ratio of the sine of that angle to the cosine of the same angle. This means that if you know the sine and cosine values for an angle, you can easily find the tangent. This relationship is significant because it shows how the ratios relate to each other, allowing us to derive one from the others, which is particularly useful in trigonometric calculations.
Examples & Analogies
Imagine you're looking at a slope (like a hill). The sine of the angle gives you the height of the hill (opposite side), and the cosine gives you the distance along the ground (adjacent side). If you want to know how steep the hill is (tangent), you can simply divide the height by the distance along the ground.
Cotangent Ratio as Cosine over Sine
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
● cot θ = \( \frac{\cos θ}{\sin θ} \)
Detailed Explanation
The cotangent of an angle (θ) is the reciprocal of the tangent. It can be expressed as the ratio of the cosine of the angle to the sine of that angle. This means that cotangent helps us understand the angle's orientation with respect to the triangle's sides, and it's another way to find relationships between the trigonometric functions.
Examples & Analogies
Think of a situation where you are trying to calculate the angle of a ladder leaning against a wall. The height to the top of the wall (cosine) compared to how far away the base of the ladder is from the wall (sine) gives you an insight into how steep the ladder is (cotangent).
Pythagorean Identity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
● sin² θ + cos² θ = 1
Detailed Explanation
This is known as the Pythagorean identity in trigonometry. It states that the square of the sine of an angle plus the square of the cosine of that angle is always equal to 1. This fundamental relationship highlights how sine and cosine values are interconnected and constrains their values, which is crucial for solving many trigonometric problems. If you know one of these ratios, you can easily find the other, provided that the angle is known.
Examples & Analogies
Imagine a unit circle, where the radius is always 1. The sine represents the height on the circle, and the cosine represents the width. The Pythagorean identity tells us that no matter where you are on this unit circle, if you square the height and the width and add them together, you will always get the radius squared (which is 1 for the unit circle).
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Tangent as the ratio of sine to cosine
-
Cotangent as the ratio of cosine to sine
-
Pythagorean identity relating sine and cosine
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
If \( \sin 30^\circ = \frac{1}{2} \) and \( \cos 30^\circ = \frac{\sqrt{3}}{2} \), then \( \tan 30^\circ = \frac{1/2}{\sqrt{3}/2} = \frac{1}{\sqrt{3}} \).
-
Using the Pythagorean identity, if \( \sin \theta = \frac{3}{5} \), then \( \cos \theta = \sqrt{1 - \left(\frac{3}{5}\right)^2} = \sqrt{1 - \frac{9}{25}} = \sqrt{\frac{16}{25}} = \frac{4}{5}. \)
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When you're stuck in a trigonometry night, Sin and Cos hold the light.
📖 Fascinating Stories
-
Imagine Tangent as a bridge that connects Sin and Cos, leading to answers in the trigonometry forest.
🧠 Other Memory Gems
-
To memorize the relationship: 'Tan is Sin over Cos, Cot flips, never at a loss.'
🎯 Super Acronyms
Tic Tac Toe
- Tangent = Sin/Cos
- Cotangent = Cos/Sin.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Tangent (tan)
Definition:
A trigonometric function defined as the ratio of sine to cosine, \( \tan \theta = \frac{\sin \theta}{\cos \theta} \).
-
Term: Cotangent (cot)
Definition:
A trigonometric function defined as the ratio of cosine to sine, \( \cot \theta = \frac{\cos \theta}{\sin \theta} \).
-
Term: Pythagorean Identity
Definition:
An identity stating that the square of sine plus the square of cosine equals one, \( \sin^2 \theta + \cos^2 \theta = 1 \).