Enrol to start learning
Reading is open to everyone. Enrolling is free, and it is what unlocks the audio lessons, practice tests and progress tracking.
7.3. Reciprocal Ratios
Interactive Audio Lesson
Unlock the classroom podcast
The transcript is above and free to read. A free account plays the conversation back.
Create a free account
Today, we will learn about the cosecant ratio. Does anyone know what the cosecant ratio represents?
Isn't it the reciprocal of sine?
Exactly! Cosecant, abbreviated as csc, is defined as the ratio of the hypotenuse to the opposite side. We can remember it as ‘C’ for ‘cosecant’ and ‘O’ for ‘Opposite’. Therefore, the formula is csc θ = 1/sin θ.
So, csc is really just the opposite side flipped?
Yes! It’s a helpful way to think about it. Let’s remember: ‘C to O’ - where C is cosecant and O is opposite.
Can you give an example of where we would use it?
Certainly! If we know the length of the hypotenuse and the opposite side in a right triangle, we can find cosecant immediately. Now let's summarize: csc θ = Hypotenuse/Opposite.
Unlock the classroom podcast
The transcript is above and free to read. A free account plays the conversation back.
Create a free account
Now that we’ve covered cosecant, let’s move on to secant. Who can tell me what secant is?
Is it the opposite of cosine, like how cosecant relates to sine?
Correct! The secant, abbreviated as sec, represents the reciprocal of the cosine function. Its formula is sec θ = 1/cos θ = Hypotenuse/Adjacent.
How do we relate it back to triangles?
Good question! In a right triangle, if you know the adjacent side and the hypotenuse, you can find secant. Remember: S for ‘Secant’ and A for ‘Adjacent’ helps us recall the relationship.
So, sec θ = Hypotenuse/Adjacent?
Absolutely! And that’s a critical relationship in trigonometry.
Unlock the classroom podcast
The transcript is above and free to read. A free account plays the conversation back.
Create a free accountFinally, we finish with cotangent. Who remembers what cotangent relates to?
It’s the reciprocal of tangent, right?
Exactly right! Cotangent, or cot, is defined as cot θ = 1/tan θ = Adjacent/Opposite.
So it’s really all about the sides in the triangle, isn’t it?
Yes! The cotangent focuses on the ratio of the adjacent side to the opposite side. Remember: C for cotangent and A for adjacent helps us remember this.
Can we do a quick recap? What are the three reciprocal ratios?
Sure! We have cosecant (csc), secant (sec), and cotangent (cot). Their definitions are based on the primary ratios. Excellent participation today!
Overview
Short Summary
Reciprocal ratios are essential trigonometric functions that relate to the primary trigonometric ratios.
Medium Summary
This section introduces the reciprocal trigonometric ratios: cosecant, secant, and cotangent, which respectively relate to sine, cosine, and tangent. Understanding these ratios helps in solving more complex trigonometric problems.
Detailed Summary
Detailed Summary of Reciprocal Ratios
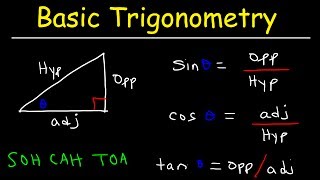
Reciprocal ratios in trigonometry are the functions that are defined in relation to the primary trigonometric ratios. For a given angle θ in a right-angled triangle, the reciprocal ratios are defined as follows:
-
Cosecant (csc): This ratio is defined as the reciprocal of the sine function. Therefore, the formula is:
-
Secant (sec): The secant is the reciprocal of the cosine function, given by:
-
Cotangent (cot): Cotangent is the reciprocal of the tangent function and is expressed as:
These ratios are fundamental in trigonometry as they provide an alternative method for solving problems and understanding relationships within triangles. Mastery of these ratios is crucial for progressing to more complex topics in trigonometry and calculus.
Reference YouTube Videos
Audio Book
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free account● Cosecant (cosec): csc θ=1/sin θ= Hypotenuse/Opposite side csc θ = \frac{1}{\sin \theta} = \frac{\text{Hypotenuse}}{\text{Opposite side}}
Detailed Explanation
Cosecant is a trigonometric function that is the reciprocal of sine. This means that it is calculated as 1 divided by the sine of an angle θ. In terms of a right triangle, if you know the length of the hypotenuse (the side opposite the right angle) and the opposite side (the side opposite the angle θ), you can find the cosecant by dividing the hypotenuse by the opposite side. Thus, cosecant is used to determine how the length of the hypotenuse relates to the opposite side of the triangle.
Examples & Analogies
Imagine you are using a ladder to reach a roof. The length of the ladder is the hypotenuse (cosecant), and the height you need to climb is the opposite side. Understanding cosecant helps you see how much longer your ladder needs to be compared to the height you want to reach.
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free account● Secant (sec): sec θ=1/cos θ= Hypotenuse/Adjacent side sec θ = \frac{1}{\cos \theta} = \frac{\text{Hypotenuse}}{\text{Adjacent side}}
Detailed Explanation
Secant is the reciprocal of cosine. This means it is calculated as 1 divided by the cosine of an angle θ. For a right triangle, it can be found by dividing the length of the hypotenuse by the length of the adjacent side (the side next to the angle θ). Therefore, secant helps us understand the relationship between the hypotenuse and the adjacent side of the triangle.
Examples & Analogies
Think of secant like using a ramp. If the ramp represents the hypotenuse, then the flat surface it rests on is the adjacent side. Secant helps us visualize how steep or flat the ramp is compared to the adjacent ground.
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free account● Cotangent (cot): cot θ=1/tan θ= Adjacent side/Opposite side cot θ = \frac{1}{\tan \theta} = \frac{\text{Adjacent side}}{\text{Opposite side}}
Detailed Explanation
Cotangent is the reciprocal of tangent. It is calculated as 1 divided by the tangent of angle θ. In a right triangle, it is determined by dividing the length of the adjacent side by the length of the opposite side. This ratio allows us to understand how the lengths of these two sides relate to each other concerning the triangle's angle.
Examples & Analogies
Consider a seesaw. If one end is the opposite side, the other end of the seesaw can be thought of as the adjacent side. The cotangent helps you assess how balanced the seesaw will be, depending on the lengths of each side.
--
Key Concepts
Examples
Step-by-step examples to apply the section's ideas and test your understanding.
Example 1: In a right triangle with a hypotenuse of 10 units and an opposite side of 6 units, the cosecant csc θ = 10/6 = 1.67.
Example 2: In a right triangle with a hypotenuse of 15 units and an adjacent side of 9 units, the secant sec θ = 15/9 = 1.67.
Example 3: In a right triangle with an adjacent side of 4 units and an opposite side of 3 units, the cotangent cot θ = 4/3 = 1.33.
Memory Aids
Interactive tools to help you remember key concepts