Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Stress and Strain
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Good morning class! Today, we are going to discuss the concepts of stress and strain. Can anyone tell me what happens to solids when external forces are applied?
They change shape or size!
Exactly! This change is described mathematically using stress and strain. Stress is defined as the force per unit area that's applied to an object. Does anyone know the formula for stress?
Yes! It's Ο = F/A, where Ο is stress, F is force, and A is the area.
Great! And what about strain? Can someone share how strain is defined?
Strain is the change in length divided by the original length. The formula is Ο΅ = ΞL/L.
Well done! Remember, stress measures how much pressure is put on a material, while strain measures how much it deforms.
Hookeβs Law
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, letβs move on to Hookeβs Law. Does anyone know what Hookeβs Law states?
It says that stress is directly proportional to strain within the elastic limit.
Correct! The mathematical expression is Ο = Eβ Ο΅, where E is Youngβs modulus. What does Youngβs modulus tell us about a material?
It indicates how stiff the material is!
Exactly! Materials with a high Young's modulus are stiff and resist deformation, whereas those with a low modulus are more pliable.
So, different materials respond differently to the same stress!
Absolutely right! Thatβs why understanding these relationships is crucial in engineering.
Types and Effects of Stress and Strain
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Next, let's discuss the different types of stress. Who can name them?
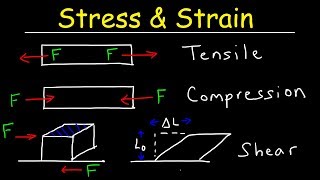
There are tensile stress, compressive stress, and shear stress.
Correct! Tensile stress is a pulling force, while compressive stress is a pushing force. Shear stress acts tangential to the surface. Now, how about strain? What types do we have?
We have linear strain, shear strain, and volumetric strain!
Good job! Linear strain measures change in length, shear strain relates to angular deformation, and volumetric strain deals with volume changes. Remember these distinctions; they reflect how materials behave under different loading conditions.
Elastic Constants and Relationships
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, letβs look at elastic constants. Can anyone tell me what Youngβs modulus is and its significance?
It's the ratio of normal stress to normal strain and indicates how stiff a material is!
Exactly! Besides Young's modulus, we also have the shear modulus and bulk modulus. What do they represent?
Shear modulus is the ratio of shear stress to shear strain, and bulk modulus is the ratio of volumetric stress to volumetric strain.
Great! Knowing the relationships between these constants helps predict material behavior under various conditions. Anyone remember the formula connecting them?
E = 2G(1 + Ξ½) and E = 3K(1 β 2Ξ½)! Where Ξ½ is Poisson's ratio!
Exactly! These equations help us understand the interplay between different mechanical properties.
Principal Stresses and Mohrβs Circle
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Finally, we will look at principal stresses and how to visualize them using Mohrβs Circle. What are principal stresses?
They are the maximum and minimum normal stresses acting on a plane when shear stress is zero.
Right! And what purpose does Mohr's Circle serve?
It helps to determine principal stresses and the orientation of principal planes.
Great! Using this graphical method aids engineers in assessing material reliability under various loading scenarios. Does anyone have questions about these concepts before we finish?
Can you remind us how to calculate average stress using the formula?
Of course! The average stress is given by Οavg = (Οx + Οy) / 2. Excellent participation today, everyone!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explores how deformable solids react to external loads, defining stress and strain, discussing Hookeβs Law, different types of stress and strain, and introducing elastic constants. It highlights the significance of these concepts in understanding material behavior under loading and deformation.
Detailed
Concept of Stress and Strain
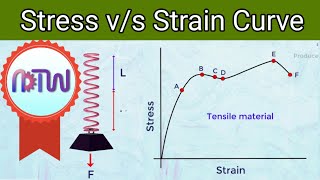
Deformable solids change shape under external forces, a behavior characterized by both stress and strain. Stress, defined as force per unit area (Ο = F/A), represents the internal response of materials to applied loads. Strain (Ο΅ = ΞL/L) quantifies deformation as a change in length relative to the original length.
Hookeβs Law
Within the elastic limit, stress is proportional to strain, expressed through the relation Ο = Eβ Ο΅, where E represents Youngβs modulus or modulus of elasticity, indicating material stiffness.
Deformation of Bars
When axial loads are applied to materials, elongation can be calculated using Ξ΄L = FL/AE. The section discusses types of stress, including tensile, compressive, and shear stress, alongside their respective equations. Similarly, it differentiates types of strain; linear, shear, and volumetric strains, each with unique implications on material behavior under stress.
Elastic Constants
Elastic constants, including Youngβs modulus (E), shear modulus (G), bulk modulus (K), and Poisson's ratio (Ξ½), relate to each other mathematically, allowing further insight into material properties.
Principal Stresses and Mohr's Circle
Principal stresses and their corresponding strains reveal the maximum and minimum stress states in materials. Mohrβs Circle provides a graphical method for visualizing these stresses, aiding in stress transformation and failure analysis.
Understanding stress, strain, and their interrelationships embodies a core concept in materials science and engineering.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Deformation and Load Response
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Deformable solids change shape or size under the action of external forces. The internal response of the material to external loading is described by stress and strain.
Detailed Explanation
Deformable solids are materials that can change their shape or size when external forces are applied. This change is referred to as deformation. Stress and strain are the two central concepts that help us understand how materials respond internally to these external forces. Stress is the internal force per unit area, while strain is the measure of deformation that occurs as a result of the applied stress. In simpler terms, stress tells us how much force a material can withstand, and strain tells us how much it has changed shape due to that force.
Examples & Analogies
Imagine a rubber band. When you pull on it, it stretches (this is strain) because you're applying a force on it (this is stress). If you pull too hard, the rubber band may snap, which shows its limit of stress.
Hookeβs Law and Basic Concepts
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Hookeβs Law: Within the elastic limit, stress is directly proportional to strain. Ο=Eβ Ο΅ Ο = E β Ξ΅ Where: β Ο: stress (N/mΒ²) β Ο΅: strain (dimensionless) β E: Youngβs modulus or modulus of elasticity.
Detailed Explanation
Hooke's Law states that as long as the material is within its elastic limit, the amount of stress applied to it will produce a proportional amount of strain. In mathematical terms, this is represented as Ο = E β Ξ΅, where Ο represents the stress in pascals (N/mΒ²), Ξ΅ is the strain (a unitless ratio of change in length to original length), and E is the Young's modulus, which is a measure of a material's stiffness. This law helps engineers understand how much a material will stretch or compress under a certain load.
Examples & Analogies
Think of a spring. When you pull on a spring, it stretches. Hooke's Law tells us that if you pull twice as hard, it will stretch twice as much as long as you donβt pull too hard and exceed its elastic limit.
Deformation of Bars under Axial Loading
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Stress: Force per unit area Ο=FA Ο = F/A β Strain: Change in length per unit original length Ο΅=Ξ΄LL Ο΅ = Ξ΄L/L β Elongation in Axially Loaded Member: Ξ΄L=FLAE Ξ΄L = FLAE.
Detailed Explanation
When an axial load is applied to a bar (like pulling or pushing), the material experiences stress, which is calculated as the applied force (F) divided by the cross-sectional area (A) of the bar. Strain describes how much the length of the material changes in relation to its original length. We use Ξ΅ = Ξ΄L/L, where Ξ΄L is the change in length and L is the original length. If you need to calculate how much a bar stretches, the formula Ξ΄L = FLAE tells you that the elongation (Ξ΄L) is the force times the original length divided by the cross-sectional area and Young's modulus of the material.
Examples & Analogies
Consider a metal rod. If you hang weights from it, the rod will stretch. You can measure how much it stretches based on the weight youβve added and the properties of the rod, including its length and thickness.
Types of Stress
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Tensile Stress: Pulling or stretching force β Compressive Stress: Pushing or squashing force β Shear Stress: Ο=FA Ο = F/A Acts tangentially to the surface.
Detailed Explanation
Stress can be classified into different types depending on how the force is applied. Tensile stress occurs when a material is stretched (like pulling a rubber band), while compressive stress is encountered when a material is being compressed or squashed (like pressing down on a sponge). Shear stress occurs when forces are applied parallel or tangential to a surface, causing layers of the material to slide past one another. Each type of stress affects materials differently and is important for understanding material behavior.
Examples & Analogies
Imagine a book on a table: the weight of the book creates compressive stress on the table below. Now, take that book and try to slide it; while doing that, you're applying shear stress. On the other hand, if you were to pull the book upwards, you would be creating tensile stress on the spine of the book.
Types of Strain
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Linear (Normal) Strain: Ο΅=ΞLL Ο΅ = ΞL/L β Shear Strain: Ξ³=tan ΞΈ Ξ³ = tan ΞΈ (angle change between planes) β Volumetric Strain: Ο΅v=ΞVV Ο΅v = ΞV/V.
Detailed Explanation
Strain also has different types that describe how materials deform. Linear (or normal) strain measures the change in length of a material compared to its original length. Shear strain involves the change in shape due to angular distortion and is calculated as the tangent of the angle change between two planes. Volumetric strain, on the other hand, measures the change in volume of an object when subjected to stress. Understanding these different strains is crucial for analyzing how structures respond to various loads.
Examples & Analogies
Think of a dough ball: when you stretch it out (linear strain), you're changing its length. If you were to push down on either side of the dough, it would change shape without changing volume (shear strain). If you put it in an airtight container and blow air into it, it increases in volume (volumetric strain).
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Stress: Represents the internal force experienced by a material divided by the area over which the force is applied.
-
Strain: The measure of deformation representing the displacement between particles in a material.
-
Hookeβs Law: The principle stating that stress is proportional to strain in an elastic material.
-
Elastic Moduli: Quantify how materials deform under stress, with Youngβs modulus focusing on linear stress-strain relationships.
-
Principal Stresses: Maximum stress on a material plane where shear stress is zero, important for failure analysis.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A steel rod undergoing tensile stress when pulled from both ends can be measured to observe elongation and strain.
-
When a column supports a weight, it experiences compressive stress, which can be calculated as the force divided by the cross-sectional area.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Stress can cause a mess, but strain tells the story, so measure don't worry!
π Fascinating Stories
-
Once upon a time, a bridge named 'Hooke' stood over a river. It learned that when pulling loads came, it had to stretch, but it always remembered the law β the more it stretched, the more it resisted!
π§ Other Memory Gems
-
For stress and strain, think 'F for force, A for area, E for elasticity' β it makes the equation!
π― Super Acronyms
S.S.E.E. means Stress, Strain, Elasticity, Effect β the journey of how materials respond!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Stress
Definition:
Force per unit area applied to a material, measured in N/mΒ².
-
Term: Strain
Definition:
Deformation experienced by a material, defined as the change in length per unit original length.
-
Term: Hookeβs Law
Definition:
A principle stating that within the elastic limit, stress is directly proportional to strain.
-
Term: Youngβs Modulus
Definition:
The ratio of normal stress to normal strain, representing the elasticity of a material.
-
Term: Principal Stresses
Definition:
The maximum and minimum normal stresses that occur in a material.
-
Term: Mohrβs Circle
Definition:
A graphical method used to determine principal stresses and shear stresses.