Bending Moments in Arch
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Bending Moments in Arches
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we’re going to explore bending moments in arches. Can anyone tell me what a bending moment is?

Isn’t it the resultant effect of forces acting on a beam or structure causing it to bend?

Exactly! In arches, bending moments also come into play due to their design and load distribution. Compared to beams, how do you think arches handle loads?

Arches mainly use compression, right?

Yes! Remember, arches operate under predominantly axial compression. This is significant because it reduces the bending moments we usually see in beams.

So, a parabolic arch would carry a load differently than a circular arch?

Great observation! A parabolic arch under uniform load is ideal as it only experiences compression, while a semi-circular one will also develop bending moments.

In summation, for arches, optimizing the shape not only accommodates loads but also minimizes bending moments. Remember PEAK: Compression, Efficiency, Axial forces, and Knowledge of forces.
Equilibrium and Forces in Arches
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, let's talk about how arches maintain equilibrium. Can anyone define equilibrium in this context?

It’s when all the forces acting on a structure are balanced, right?

Correct! In arches, we often look at vertical and horizontal reactions. Can someone give me an example of how we might calculate these?

Using the formula for vertical reactions based on load distribution?

Yes! The vertical reaction in an arch can typically be determined as V = wL, where w is the load per unit length and L is the span length. Remember, in a three-hinged arch, there’s no shear at midspan. This ensures equilibrium.

Does this mean there are points where bending can still happen?

Absolutely! In arches with two hinges or none, moments can occur at supports or crowns. Always think of stability in design.

To summarize: Ensure that you understand how to balance loads when designing an arch. Remember this phrase: BALANCED - Bending, Axial forces, Loads, and Equilibrium.
Design Considerations for Arches
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s discuss design considerations for arches. Why do you think the height of an arch is significant?

Is it because taller arches can better distribute loads?

Exactly! A higher rise means lower horizontal thrusts, which stabilizes the arch. What is a common span-to-rise ratio in architecture?

I think it’s typically between 5 to 12?

Correct again! But remember, if the rise is too high, it could lead to buckling. Design must also consider aesthetics, utility, and materials. How about the materials used in arches?

Usually stone or masonry, since they resist compression well?

Precisely! A well-designed arch minimizes moments and maintains integrity under load. Always think of the SLEEK concept: Shape, Load, Enhancements, Efficiency, and Knowledge.
Examples of Bending Moments in Arches
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s look at some examples of arches. Can anyone explain what happens to a semi-circular arch under its own dead weight?

We need to integrate the load over the entire structure for reactions.

Right! To solve, we will determine vertical and horizontal reactions using equilibrium equations. What’s one of those equations?

M = 0; we can set the moments around point A.

Absolutely! After calculating reactions, check the sum of moments to validate your design. Practice with problem sets to ensure you understand. Think of this acronym: REACT – Reactions, Equilibrium, Analysis, Calculations, Tension.

What about when live loads are also applied?

Good question! Live loads can complicate the load path, and it’s important to assess how these affect moment calculations at various points.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section illustrates the fundamental principles of bending moments in arches, discussing equilibrium conditions, the significance of internal forces, and how structural design can optimize arch shapes to reduce moments and enhance stability.
Detailed
Bending Moments in Arch
This section explores the analysis of bending moments in arches, emphasizing their significance in structural engineering. Arches are unique in how they handle loads, primarily through axial compression while also resisting bending moments when necessary. The section introduces polar coordinates for analytical equations, indicating a shift from traditional Cartesian approaches. It outlines how a parabolic arch carries uniform loads in compression only, contrasting this with a semi-circular arch that experiences flexural stresses in addition to compressive ones. A critical aspect discussed is the optimization of arch shape to align with bending moments to enhance structural efficiency. Furthermore, the text examines the implications of arch geometry on stress distribution and the existence of bending moments at hinges, showcasing practical examples involving three-hinged arches. The section concludes with a summary of the importance of high-rise arches for effective load distribution and the challenges posed by varying loads.
Youtube Videos
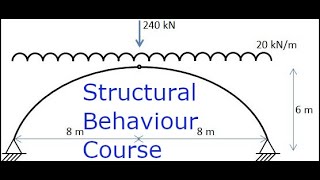



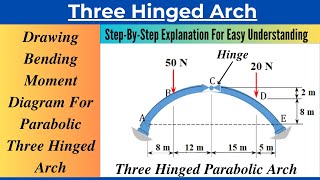



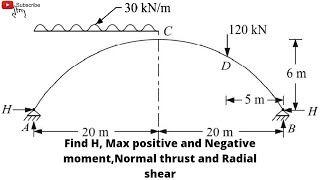
Audio Book
Dive deep into the subject with an immersive audiobook experience.
The Role of Bending Moments in Arches
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If the arch has only two hinges, or if it has no hinges, then bending moments may exist either at the crown or at the supports or at both places.
Detailed Explanation
In arch structures, if there are only two hinges, or if there are no hinges at all, bending moments can occur. These moments produce stress at different points of the arch, particularly at the crown (the topmost point of the arch) and at the support points. Bending moments indicate how much the arch is trying to rotate at these points due to loads applied to it.
Examples & Analogies
Imagine holding a long, flexible stick at both ends and pressing down in the middle; the stick bends and experiences strain at the supports (your hands) and the center (the crown). Similarly, the arch's structure reacts under load and bends, leading to moments at the crown and supports.
Importance of Arch Rise and Spans
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Since H varies inversely to the rise h, it is obvious that one should use as high a rise as possible. For a combination of aesthetic and practical considerations, a span/rise ratio ranging from 5 to 8 or perhaps as much as 12, is frequently used. However, as the ratio goes higher, we may have buckling problems, and the section would then have a higher section depth, and the arch advantage diminishes.
Detailed Explanation
The height or rise (h) of the arch influences its overall stability. A higher rise generally results in lower horizontal thrust (H), which is beneficial in maintaining the structure's integrity. Engineers often aim for a span-to-rise ratio between 5 and 12, balancing aesthetics and practicality. However, increasing this ratio too far can lead to structural issues, such as buckling, which compromises the arch's advantages.
Examples & Analogies
Think of a bridge made of a tall, graceful arch. The higher the arch, the less it tries to push outward, making it more stable. However, if the arch is made too tall compared to its width, it might sway or buckle under pressure, similar to a tall tree that bends in the wind.
Practical Considerations for Real-Life Arches
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In a parabolic arch subjected to a uniform horizontal load there is no moment. However, in practice an arch is not subjected to uniform horizontal load. First, the depth (and thus the weight) of an arch is not usually constant, then due to the inclination of the arch the actual self-weight is not constant. Finally, live loads may act on portion of the arch, thus the line of action will not necessarily follow the arch centroid. This last effect can be neglected if the live load is small in comparison with the dead load.
Detailed Explanation
Theoretically, a parabolic arch without external loads should experience no moments. However, real-world conditions complicate this situation. The weight of the arch is not consistent due to varying depths, and loads (like vehicles or snow) may not be uniformly distributed. These factors cause bending moments, altering the theoretical expectations. If additional loads are minimal compared to the arch's weight, the effects can often be disregarded.
Examples & Analogies
Consider a heavy slide at a playground. When children play on it, their weight is unevenly distributed along the slide's length, affecting how it bends and flexes. Similarly, real arches experience loads that make them behave differently than we might calculate with simple theory.
Key Concepts
-
Bending Moment: The internal moment that resists external loads and can cause deformation.
-
Axial Compression: A force that compresses materials along their length, crucial for arches.
-
Equilibrium: The balance of forces ensuring stability in structural design.
-
Parabolic vs. Semi-Circular: Different arch shapes that affect bending stress and load distribution.
-
Design Optimization: The process of determining the ideal shape and materials for efficient load transfer.
Examples & Applications
An example of a parabolic arch is the Gateway Arch in St. Louis, which effectively distributes its load through compression.
A semi-circular arch example is the Colosseum in Rome, showcasing both compressive and bending stresses.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Arches stand with grace and might, compressing loads both day and night.
Stories
Imagine an architect who designs an arch; his motto is to embrace compression's arch! With every rise, he finds a balance, leading to structures that stand as a challenge.
Memory Tools
ARM - Arch, Reaction, Moment - helps remember key aspects related to arches in loading.
Acronyms
CLEAN - Compression, Load, Equilibrium, Axial stress, Normal forces – key concepts to remember for arch analysis.
Flash Cards
Glossary
- Bending Moment
The internal moment that occurs within structures due to external loading, causing rotation about a point or axis.
- Axial Compression
A type of internal force that results in materials being shortened along the axis of the applied load.
- Equilibrium
A state in which the sum of forces and moments acting on a structure is zero, indicating a balanced condition.
- Parabolic Arch
An arch shape characterized by a parabolic curve, optimized to distribute uniform loads in compression.
- SemiCircular Arch
An arch with a semi-circular profile, which can experience both compressive and bending stresses.
- ThreeHinged Arch
A statically determinate arch with three supports that can accommodate movement and prevent internal stresses.
Reference links
Supplementary resources to enhance your learning experience.
