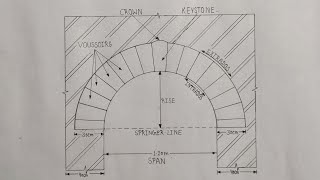
Example 7-2: Semi-Circular Arch
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Semi-Circular Arches
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're delving into semi-circular arches. Does anyone know what defines a semi-circular arch?

Is it an arch that looks like a half-circle?

Exactly! It has a crescent shape and is effective in supporting loads via compression. Can anyone explain why compression is preferable for such structures?

Because materials like stone and masonry work well under compression rather than tension?

Correct! Now, let’s talk about the basic forces acting on this arch, specifically its dead weight.
Load Distribution on the Arch
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

When we load a semi-circular arch, how do we distribute that weight?

Is it evenly distributed along the arc?

Yes! The dead weight is applied uniformly, which helps us create accurate calculations. Let’s now calculate the vertical reactions.

How do we find the vertical reactions, by integrating the weight over the arc?

Correct! Integration helps us sum the moments. Remember, equilibrium is key here.

What happens if the loading isn’t uniform?

Great question! Non-uniform loads change the analysis; we often use fixed relationships to approximate. But let’s stay focused on uniform loading for now.
Calculating Reactions
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let’s derive the vertical reaction for the arch. Can anyone outline the first step?

We use the moment equilibrium formula to start?

Yes! We must consider all forces acting at the supports. This requires integrating our loads. Let’s write down the equation for vertical reactions.

Is the moment arm important in this equation?

Absolutely! The moment arm is crucial for calculating resultant forces accurately. Let’s see how we can solve for the vertical reaction using the equation.
Analyzing Horizontal Reactions
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Having calculated the vertical reactions, what about horizontal reactions? How are they determined?

Are they derived from the same loading conditions?

Yes! They also depend on the angle of application due to the circular geometry. Let’s look at how to compute them.

What does integrating tell us about horizontal loads?

Great point! We understand their influence through integration, ensuring the sum of horizontal pressures aligns with structural stability.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we study the three-hinged semi-circular arch. The behavior of the arch under its own dead load is analyzed, with derivations for vertical and horizontal reactions, demonstrating how to manage forces within the structure effectively.
Detailed
Example 7-2: Semi-Circular Arch
This section explores the critical aspects of the semi-circular arch, particularly focusing on how it behaves under its own dead weight. A three-hinged arch is statically determined and showcases unique properties when subjected to loads. The vertical and horizontal reactions at the points of support are derived from the integration of forces acting at the arch along with the moment equilibrium equations.
Key Points:
- The vertical reaction is calculated first, ensuring that moment equilibrium conditions are satisfied by integrating the load along the semi-circular outline of the arch.
- The entire structure's reactions are determined systematically, showcasing the importance of understanding the physical distribution of loads in an arch structure.
- The significance of proper structural design and analysis is highlighted, ensuring stability and performance using static equilibrium principles.
Youtube Videos









Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding the Structure
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Determine the reactions of the three hinged statically determined semi-circular arch under its own dead weight w (per unit arc length s, where ds = rdϕ).
Detailed Explanation
In this part, we are looking to analyze a three-hinged semi-circular arch, which is a common type of arch used in construction. The arch is supported at three different points (hinges), allowing it to flex under load. It carries a dead weight denoted as 'w', representing the weight per unit length of the arch. The term 'per unit arc length s' means we will consider how the weight affects each segment of the arch as we move along its curve.
Examples & Analogies
Think of this arch as a rainbow shaped perfectly over a playground. The hinges at either end and the center allow the rainbow to flex and adjust based on how much 'weight' (like the children hanging on it) is applied to it. Just like the rainbow can hold itself up while accommodating some weight, the arch does the same.
Finding Vertical Reactions
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Solution: 1. Vertical Reaction is determined first:
\[ (\sum M = 0) ; (C_y)(2R)+ wR dϕ R(1+cos(ϕ)) = 0 \]
Detailed Explanation
To find the vertical reaction force at point C (one of the hinges), we sum the moments around that point to set the net moment to zero, ensuring equilibrium. The formula includes the reaction force at C (C_y) multiplied by the distance (2R), and the applied load integrated over the arch, considering the angle (ϕ) at which the load is acting. By solving the equation, we can find how much force needs to be exerted in a vertical direction to keep the structure stable.
Examples & Analogies
Imagine you are holding a seesaw with a friend sitting on one end. To keep it balanced (equilibrium), you need to exert an upward force proportional to their weight. The same principle applies here: we calculate how much upward force (reaction) should be applied at point C to keep the semi-circular arch from tipping over.
Finding Horizontal Reactions
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
- Horizontal Reactions are determined next:
\[ (\sum M = 0); (C_x)(R)+(C_y)(R) - wR dϕ R cos(ϕ) = 0 \]
Detailed Explanation
Next, we will find the horizontal reaction forces at the hinges. Here, we similarly sum up the moments about hinge C but this time we focus on the horizontal components of the forces. The equation shows how much horizontal support (C_x) is needed to counteract the lateral forces generated by the weight acting at an angle due to the curvature of the arch. Just like with vertical reactions, solving this equation gives us the necessary horizontal force for balance.
Examples & Analogies
Picture holding a large beach ball. As it resists rolling away, your hands must apply horizontal force to keep it in place. In this scenario, the horizontal reaction force at the hinges acts like your hands, preventing the arch from shifting out of position due to the weight above.
Key Concepts
-
Three-Hinged Arch: A configuration of arch that allows movement and simplifies the analysis of internal forces.
-
Load Management: Understanding how loads interact with the structure is critical for ensuring its integrity.
-
Static Equilibrium: Essential concept to ensure that the arch does not rotate or move unexpectedly under load.
Examples & Applications
Example of a bridge using a semi-circular arch, showcasing load distribution during construction and operation.
A famous structure like the Colosseum, which employs elements of both semi-circular and full arches in its design.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Arches may be twisted and bent, but through compression, their strength is sent.
Stories
Imagine a town where the main road is an arch. On hot days, it expands a bit, but because it’s built with hinges at the base, it can handle that change effortlessly.
Memory Tools
To remember loads in arches, think 'COLD' - Compression, Optimum Load Distribution.
Acronyms
ARCH can stand for 'A Structural Curve Holding'.
Flash Cards
Glossary
- SemiCircular Arch
An arch that has a curvature in the shape of a half-circle, mainly used to span the space or support loads by compression.
- Vertical Reaction
The force exerted vertically by the supports of an arch in response to loads applied.
- Horizontal Reaction
The force that acts horizontally at the supports due to loads on the arch.
- Load Distribution
The manner in which a load is shared or spread across a structure.
- Moment Equilibrium
A condition where the sum of moments acting on a body is zero, resulting in static equilibrium.
Reference links
Supplementary resources to enhance your learning experience.
