Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Theveninβs Theorem
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today we will talk about Theveninβs theorem, which states that any linear electrical network can be reduced to a single voltage source and a single resistor. Can anyone tell me why this is beneficial?
I think it makes the circuit easier to analyze, especially if there are many components involved.
Exactly! It simplifies our calculations. By using Theveninβs theorem, we can look at amplifiers more easily when we translate them into equivalent circuits.
So, how do we apply this to amplifiers specifically?
Great question! We often start with finding the small signal equivalent circuit. The transistor, for example, can be replaced with a dependent current source.
What does that mean for the analysis of the amplifier?
It means we can calculate the gain and choose components based on that simplified modelβletβs move on to practical examples.
Small Signal Models
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's dive into small signal models. In a common source amplifier, we have a voltage-dependent current source. Can anyone explain what that means?
Itβs a current that depends on the voltage at the gate, right?
Exactly! This is crucial when we calculate our output voltage. If we express this as a transconductance, we can map it to our Thevenin equivalent easily.
What are the main things weβll look at while doing this?
Youβll want to identify resistances and capacitors as they impact our gain and frequency response. Always remember R and C configurations.
So, all the components in series or parallel will affect the output?
Yes! R and C arrangements form critical parts of our R-C or C-R circuits influencing cutoff frequencies.
Frequency Response
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's discuss frequency response! Who can remind us what R-C circuits do with frequency?
R-C circuits can define cutoff frequencies for either high or low pass signals.
Right! The lower cutoff frequency is influenced by the C-R circuit while the upper cutoff comes from R-C configurations. How do we calculate these?
Is it based on the values of R and C?
Exactly! The actual values will give us important insights into our gain profile across frequencies. Itβs all about knowing which parts contribute.
How can we visualize this clearly?
We can plot Bode plots! They will help us understand gain versus frequency visually.
Cutoff Frequencies
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
How many of you remember the significance of cutoff frequencies for our amplifiers?
I think they determine what frequencies the amplifier can effectively amplify.
Correct! They tell us where our amplifier starts limiting the performance. What happens if we design incorrectly?
We might lose signal quality or not amplify the desired range?
Exactly! Thatβs why understanding these concepts is critical before we choose and place our components in real applications.
How can we ensure our designs are robust?
We can simulate or prototype and check the frequency response to validate our design choices.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section elaborates on Thevenin's theorem and how it helps simplify complex circuits into manageable equivalents, focusing on small-signal models and frequency responses in common source and common emitter amplifiers.
Detailed
Thevenin Equivalent and Circuit Translation
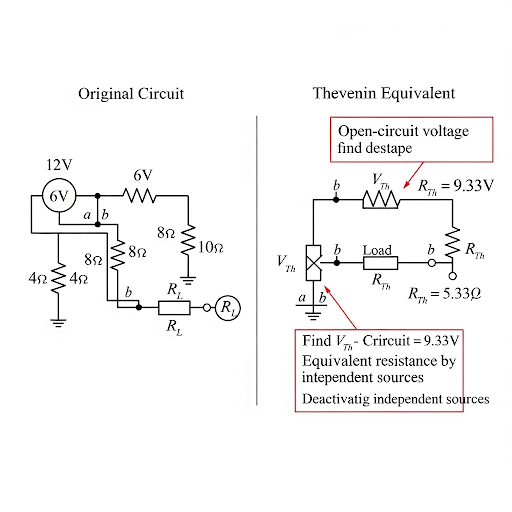
This section explores the concept of Thevenin's equivalent circuit within the context of analog electronic circuits, specifically focusing on amplifiers. It explains how Thevenin's theorem simplifies the analysis of amplifiers by converting them into a simpler equivalent circuit. The section begins with a description of the block components of amplifiers, such as capacitors and resistors, and how these elements can be transformed into Thevenin equivalents.
Key Points:
- Amplifier circuits can be modeled using Theveninβs theorem, which allows for complex circuit simplifications.
- The analysis includes small-signal models where the transistor is replaced with its small signal equivalent (a voltage-dependent current source).
- The frequency response of the amplifiers is influenced by R-C and C-R circuits, which contribute to the cutoff frequencies.
- The discussion frequently returns to the unified model, helping connect the theory with practical applications in amplifier design. The importance of determining the upper and lower cutoff frequencies is emphasized, as these affect the gain and overall performance of the amplifier.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding the Amplifier Configuration
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, say to start with we do have common source amplifier and the circuit is given here. The circuit is given here for your reference and if you see here we do have the main part main amplifier here and then, we are feeding the signal through this capacitor called say C. At the output we are observing the signal after removing the DC part through the C.
Detailed Explanation
In this chunk, we introduce the concept of a common source amplifier configuration. This amplifier setup takes an AC signal input and uses a capacitor (C) to couple the input signal. Coupling capacitors often block DC signals, allowing only AC signals to pass. This is essential for amplifying small AC signals in electronic circuits. Understanding this configuration is the first step in analyzing the amplifier's behavior.
Examples & Analogies
Imagine a water pipe where only certain types of water (like dirty water) need to be filtered out while clean water (like AC signals) flows through. The capacitor works like a filter; it allows only the clean, desired AC signals to pass while blocking any unwanted direct current.
Small Signal Equivalent Circuit
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If we draw the small signal equivalent circuit after obtaining the quiescent point and other things are defined by R , R ; then, V and R. What we obtained in our previous discussion we say that at the middle, at the middle we got the main amplifier circuit and here of course, it is the small signal equivalent circuit; where, V it is V node, it is AC ground.
Detailed Explanation
This chunk describes the small signal equivalent circuit model used to analyze the amplifier. When we want to study the circuit's behavior for small AC signals, we replace large signal elements with their corresponding small-signal models. The AC ground concept indicates that a certain point in the circuit is considered zero volts for AC analysis, simplifying calculations. The elements R1 and R2 refer to resistances in the circuit affecting signal behavior.
Examples & Analogies
Think of it like adjusting your microphone settings when singing. When the audio is soft (small signal), the equipment works differently than when you're belting (large signal). Just as you adjust with smaller knobs for greater precision, we simplify our circuit to examine only the 'small' electrical responses for effective analysis.
Transconductance**: Understanding the Core Concepts
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The transistor it is getting replaced by its small signal model which is voltage dependent current source called i . And its expression it is given by transconductance g Γ v . v is the voltage appearing across gate to source of the transistor.
Detailed Explanation
Here, we discuss the concept of transconductance (gm), showing how the transistor's behavior can be characterized with a dependent current that flows based on the input voltage (vg). This concept is critical for understanding the amplifier's performance, as it indicates how effectively the amplifier can convert voltage changes to current changes. The mathematical relationship illustrates that the higher the transconductance, the more current can be generated for a given input voltage, indicating good amplifying capabilities.
Examples & Analogies
Imagine a water tap (transistor) that opens wider (increased transconductance) as you turn it (voltage input), allowing more water (current output) to flow. A highly responsive tap lets you control the flow more easily, just like a transistor's ability to amplify signals increases with higher transconductance.
Thevenin Equivalent Conversion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, based on this v, we are getting this current and then that current it is flowing through this R and then, of course, we are getting a voltage here. Note that still this is not on equivalent, but it can be easily converted into Thevenin equivalent, namely we can make the amplifier which is having a gain of β g Γ R.
Detailed Explanation
In this section, we explore converting the circuit into its Thevenin equivalent form, which simplifies circuit analysis. The Thevenin equivalent circuit consists of a voltage source (representing the output voltage developed by the amplifier times the gain) in series with a resistance (representing the internal resistance of the amplifier). This simplification is particularly useful for analyzing how the amplifier interacts with other connected components or stages.
Examples & Analogies
Think of it like summarizing a book into an essential overview. Instead of explaining each chapter, you provide key plot points and character roles (Thevenin equivalent). This helps your audience grasp the main story quickly and understand how it connects to other stories they might know.
Output and Input Port Translation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Likewise, input side again this two part these two resistors you can translate into equivalent resistance here, which it will be R β«½ R . So, what we can see here that C ; this C . So, this is the C and then, this R which is R β«½ R , they are forming one C-R circuit.
Detailed Explanation
This chunk discusses how the resistances on the input side can be combined into an equivalent resistance, allowing us to analyze the amplifier's input characteristics systematically. Additionally, describing the capacitive elements, we explore how the combinations of resistors and capacitors form C-R circuits and R-C circuits, helping to demonstrate the frequency response of the amplifier. Understanding these configurations enables engineers to predict how the amplifier will behave in real situations.
Examples & Analogies
Think of it in terms of a network of roads where each road (resistor) can be interpreted as part of a larger route (circuit). The routes can be combined to form a simplified map (equivalent resistance), helping drivers (engineers) understand how to navigate the intersections (connections) more effectively.
Final Amplifier Model and Frequency Response
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, what we are getting here? It is that the amplifier, it can be translated into that unified model which we have discussed just now, before the short break; where, it is having C , then R and then across this R the voltage it is v and that v, it is generating a voltage.
Detailed Explanation
In this concluding section, we summarize how the amplifier's components translate into a unified model that captures both frequency response and gain characteristics. This model enables engineers to see how different passive components affect the frequency behavior of the amplifier, identifying contributions to both cutoff frequencies and gain. This understanding is crucial when designing amplifiers for specific applications such as audio equipment or communication devices.
Examples & Analogies
Imagine a recipe (the amplifier model) that relies on specific ingredients (C and R components) to deliver the final dish (output voltage). Understanding how each ingredient affects the flavor (gain and frequency response) helps chefs (engineers) create the best dish possible for their diners (end-users) in various situations.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Thevenin Equivalent: A simplified model consisting of a voltage source and a resistance to analyze complex networks.
-
Small Signal Model: A linear approximation of non-linear devices for easy analysis.
-
Cutoff Frequency: Defines limits of frequency response, affecting the signal amplification range.
-
Transconductance: Key parameter that defines the gain of voltage amplifiers.
-
Bode Plot: Visual tool to demonstrate how gain and phase shift change with frequency.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a common source amplifier, the output voltage can be calculated using the small signal model where the gain is expressed as -g * R.
-
For a simple R-C circuit, the lower cutoff frequency can be calculated using the formula fc = 1/(2ΟRC).
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
In Theveninβs hand, a voltage and resistance stand, simplifying circuits, making analysis grand.
π Fascinating Stories
-
Imagine a wise old professor, Thevenin, who can reduce complex circuits to a simple story with just a voltage and resistance that aids in understanding.
π§ Other Memory Gems
-
For Thevenin: 'Voltage Equals Resistance'; remember itβs always about simplifying!
π― Super Acronyms
TRC
- Thevenin's Reduced Circuit.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Thevenin Equivalent
Definition:
A simplified representation of a complex circuit as a single voltage source and series resistance.
-
Term: Small Signal Model
Definition:
A representation of a nonlinear device as a linear approximation around a certain operating point.
-
Term: Cutoff Frequency
Definition:
The frequency at which the output signal is reduced to a specific amount, typically -3 dB from the maximum.
-
Term: Transconductance (g)
Definition:
The ratio of the output current to the input voltage in the small signal model, representing the performance of the transistor.
-
Term: Bode Plot
Definition:
A graphical representation of a system's frequency response, showing gain and phase versus frequency.