GRAVITATIONAL POTENTIAL ENERGY
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Concept of Gravitational Potential Energy
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will explore the concept of gravitational potential energy. Can anyone tell me what we mean by potential energy?

Is it the energy stored in an object due to its position?

Exactly! Gravitational potential energy is the energy stored in an object due to its position within a gravitational field. A common example is lifting a book off the floor. The work done against gravity to lift the book increases its potential energy.

How do we calculate that energy?

Great question! The potential energy formula near Earth's surface is given by W = mgh, where 'm' is mass, 'g' is acceleration due to gravity, and 'h' is the height. It means higher you raise it, more potential energy it has.

But what happens when we consider larger distances, like from the Earth itself?

When considering larger distances, we have to use the gravitational formula involving distance from Earth's center. This shows how gravitational force and potential energy change as you move further away.

To remember this, think of 'GPS': Gravitational Potential with Scale. Remember that gravitational potential varies with height and distance!

Now, let's recap! Gravitational potential energy increases as an object is lifted, and the formula is influenced by both height and mass. Who can give me the formula for potential energy?

W = mgh! But what about when we go beyond height measurements?

Great! Beyond height, we use gravitational force equations influenced by mass and distance. Let’s keep exploring!
Work Done Against Gravity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's discuss the work done against gravity. Can anyone explain how work relates to gravitational potential energy?

It's about how much energy is needed to lift something?

Exactly! The work done on lifting an object results in increased gravitational potential energy. Can someone give me the formula we mentioned earlier?

W = mg(h2 - h1)!

Perfect! This equation tells us the total work done when moving an object from one height to another. Now, what if we have an object moving much farther from the Earth?

We'll have to use the integral of the gravitational force!

"Correct! As the gravitational force varies with distance, we calculate the work done using the integral form.

What does the negative sign mean?

Great observation! The negative sign indicates that work is done against the gravitational force as you lift the object away from the gravitational source.

Recap: The work is done against gravity, and increases potential energy. Remember that in deeper calculations, we use integrals!
Applications of Gravitational Energy
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today let's apply what we learned about gravitational potential energy. Why do we care about calculating it with celestial mechanics?

It helps us understand how planets, moons, and other bodies move under gravity!

Exactly! The interactions between celestial bodies involve gravitational potential energy. When we calculate energy in the context of astrological bodies, we use the gravitational potential between them. Can anyone recall that formula?

It's V = -G(m1 * m2)/r!

Well done! This equation helps us find the gravitational potential energy between two masses, which is crucial in understanding orbits, space travel, and more.

So, does that mean we can design rockets using this knowledge?

Absolutely! By understanding gravitational forces and energies, engineers can optimize the paths of rockets to maximize efficiency.

Remember: GPE connections to motion help us figure paths in space! Any clarification needed?
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section discusses the concept of gravitational potential energy, explaining its dependence on height in a uniform gravitational field and detailing how it changes as an object is moved within the gravitational field created by a celestial body, such as Earth. The importance of understanding potential energy in gravitational contexts is also emphasized.
Detailed
Gravitational Potential Energy
Gravitational potential energy (GPE) is defined as the work required to move an object within a gravitational field, especially when lifting it against the force of gravity. Since gravity is a conservative force, the work done is independent of the path taken. This section outlines the calculations and implications of gravitational potential energy near the Earth's surface and at varying distances from it.
Key Concepts:
- When an object is lifted to a height h within Earth's gravitational field, the potential energy gained (or the work done against gravity) can be calculated using the formula:
$$ W_{12} = mg(h_2 - h_1) $$
- The gravitational potential energy W at height h above Earth's surface is given by:
$$ W(h) = mgh + W_0 $$
where W_0 is a constant representing potential energy at a reference level (usually taken as 0 at the surface).
- In cases involving significant distances from Earth, we need to use the gravitational force equation:
\[ F = \frac{G M_E m}{r^2} \]
where ME is the mass of the Earth and r is the distance from the center of Earth to the mass m. Thus, the work done from height r1 to r2 is computed by integrating the force:
\[ = -G M_E m \left( \frac{1}{r_2} - \frac{1}{r_1} \right) \]
- The gravitational potential energy between masses m1 and m2 separated by a distance r is denoted as:
$$V = -\frac{G m_1 m_2}{r} \quad \text{(if we choose } V = 0 \text{ as } r \to \infty)$$
This understanding of gravitational potential energy is crucial as it aids in calculating the energy dynamics in celestial mechanics and understanding how bodies interact within gravitational fields.
Youtube Videos








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Gravitational Potential Energy
Chapter 1 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
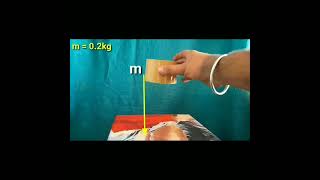
We had discussed earlier the notion of potential energy as being the energy stored in the body at its given position. If the position of the particle changes on account of forces acting on it, then the change in its potential energy is just the amount of work done on the body by the force.
Detailed Explanation
Gravitational potential energy refers to the stored energy of an object based on its height above the ground or its position in a gravitational field. When we lift an object against gravity, we do work on it. The work done on the object is stored as potential energy. Thus, the potential energy changes when the object's position changes due to the force of gravity acting upon it.
Examples & Analogies
Imagine holding a ball in your hand above the ground. The higher you lift the ball, the more work you do on it, and the more potential energy it gains. If you let go, the potential energy converts into kinetic energy as the ball falls.
Work Done by Gravity
Chapter 2 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
As we had discussed earlier, forces for which the work done is independent of the path are the conservative forces. The force of gravity is a conservative force and we can calculate the potential energy of a body arising out of this force, called the gravitational potential energy.
Detailed Explanation
Conservative forces allow us to calculate work done in a specific way, where the work depends only on initial and final positions, not the path traveled. Gravity is such a force. The gravitational potential energy can be expressed with the familiar equation W = mgh, where 'W' is the potential energy, 'm' is mass, 'g' is acceleration due to gravity, and 'h' is height above a reference point.
Examples & Analogies
Think of a rollercoaster at the top of a hill. The potential energy of the rollercoaster is at its maximum when it's at the highest point. As it descends, this energy transforms into kinetic energy, leading to a thrilling ride downwards.
Potential Energy Near Earth's Surface
Chapter 3 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Consider points close to the surface of earth, at distances from the surface much smaller than the radius of the earth. In such cases, the force of gravity is practically a constant equal to mg, directed towards the centre of the earth.
Detailed Explanation
Near the Earth's surface, gravity can be considered constant (approximately 9.8 m/s²) for small heights, enabling simpler calculations of potential energy. If you have two heights, h1 and h2, the work done to lift an object from h1 to h2 is calculated directly using the potential difference: W = mg(h2 - h1).
Examples & Analogies
If you’re lifting a backpack from the floor to a table, the force required (weight of the backpack) multiplied by the height difference is the work done against gravity.
Potential Energy at Arbitrary Heights
Chapter 4 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If we consider points at arbitrary distance from the surface of the earth, the result just derived is not valid since the assumption that the gravitational force mg is a constant is no longer valid.
Detailed Explanation
Once you move far enough away from Earth, the gravitational force decreases according to the inverse square law. This means the potential energy must be calculated using a different formula involving the mass of the Earth and the distance from its center: W = -G(Mm)/r. This formula shows that potential energy becomes a function of distance from the Earth's center rather than just height.
Examples & Analogies
Think of launching a spacecraft into orbit. As it moves further from Earth, the gravitational pull weakens, and the spacecraft has to reach a specific velocity to maintain its orbit without falling back.
Conventions in Potential Energy Measurement
Chapter 5 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
One conventionally sets W1 equal to zero, so that the potential energy at a point is just the amount of work done in displacing the particle from infinity to that point.
Detailed Explanation
In physics, we often define potential energy based on a reference point, often choosing infinity (far away from any gravitational influence) as a zero point for potential energy. This means that the potential energy at a certain point is the energy associated with bringing a mass from infinity to that point.
Examples & Analogies
Imagine climbing a mountain: your potential energy increases as you gain height, and if you were to drop a stone from the top back to the ground, you're sending it back to a point where it possesses no potential energy comparatively.
Potential Energy of Two Masses
Chapter 6 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
We have calculated the potential energy at a point of a particle due to gravitational forces on it due to the earth and it is proportional to the mass of the particle. The gravitational potential due to the gravitational force of the earth is defined as the potential energy of a particle of unit mass at that point.
Detailed Explanation
The gravitational potential energy between two masses is determined by their masses and inversely by the distance separating them. The more massive the objects, the stronger the potential energy field they create. This helps in understanding the gravitational interactions not just of Earth with an object, but also between two objects in space.
Examples & Analogies
Consider two people on a seesaw. If one is significantly heavier than the other, the heavier person will have more influence on the seesaw's balance, just like how a larger mass affects gravitational potential energy.
Example: Potential Energy of Four Particles
Chapter 7 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Example 7.3: Find the potential energy of a system of four particles placed at the vertices of a square of side l. Also obtain the potential at the centre of the square.
Detailed Explanation
This example highlights how gravitational potential energy depends on the configuration of multiple particles. By calculating the potential energy based on distances between each pair of particles, students can grasp how energy interacts in a system rather than just between two single masses.
Examples & Analogies
Think of friends lifting each other up in a line: their combined effort (potential energy) can change dramatically based on how close they are to one another and where they are in the line.
Key Concepts
-
When an object is lifted to a height h within Earth's gravitational field, the potential energy gained (or the work done against gravity) can be calculated using the formula:
-
$$ W_{12} = mg(h_2 - h_1) $$
-
The gravitational potential energy W at height h above Earth's surface is given by:
-
$$ W(h) = mgh + W_0 $$
-
where W_0 is a constant representing potential energy at a reference level (usually taken as 0 at the surface).
-
In cases involving significant distances from Earth, we need to use the gravitational force equation:
-
\[ F = \frac{G M_E m}{r^2} \]
-
where ME is the mass of the Earth and r is the distance from the center of Earth to the mass m. Thus, the work done from height r1 to r2 is computed by integrating the force:
-
\[ = -G M_E m \left( \frac{1}{r_2} - \frac{1}{r_1} \right) \]
-
The gravitational potential energy between masses m1 and m2 separated by a distance r is denoted as:
-
$$V = -\frac{G m_1 m_2}{r} \quad \text{(if we choose } V = 0 \text{ as } r \to \infty)$$
-
This understanding of gravitational potential energy is crucial as it aids in calculating the energy dynamics in celestial mechanics and understanding how bodies interact within gravitational fields.
Examples & Applications
Lifting a book off a shelf increases its gravitational potential energy, calculated using W = mgh.
Calculating the potential energy of an object at varying distances from Earth using W_{G} = - rac{GM_E m}{r}.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Lift it high, it shall fly, energy stored by reaching the sky!
Stories
Imagine a bird that rises into the sky. The higher it flies, the more energy it gains, just like how lifting a ball increases its potential energy.
Memory Tools
Remember 'GPE': G for Gravity, P for Potential, E for Energy—a memory jogger!
Acronyms
GPS
Gravitational Potential with Scale—think about height and energy!
Flash Cards
Glossary
- Gravitational Potential Energy
The energy stored in a mass based on its height within a gravitational field.
- Conservative Force
A force where the work done is independent of the path taken.
- Work Done
The energy transferred when a force acts on an object over a distance.
- Force of Gravity
The attractive force between two masses.
- Mass
The amount of matter in an object, which influences gravitational force.
- Distance
The spatial relationship between two points, important in calculating gravitational effects.
Reference links
Supplementary resources to enhance your learning experience.
