Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Kepler's First Law
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today we'll explore Kepler's First Law, which states that all planets move in elliptical orbits with the Sun at one focus. Can anyone tell me what an elliptical orbit is?
Is it like a stretched-out circle?
Exactly! An ellipse looks like a flattened circle. Let’s picture it: if we take a string and pin two points on a board, and use a pencil keeping the string taut, we can draw an ellipse. What do we call the closest and farthest points from the Sun in an ellipse?
The closest point is the perihelion and the farthest is the aphelion.
Right! This means that planets speed up when closer to the Sun and slow down further away. Remember this with the phrase: 'Closer is quicker!'
What about comets? Do they also have elliptical orbits?
Yes! Comets have highly elliptical orbits. Great question! Now, let’s summarize: Kepler’s First Law tells us about the path of planetary orbits and introduces perihelion and aphelion.
Kepler's Second Law
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
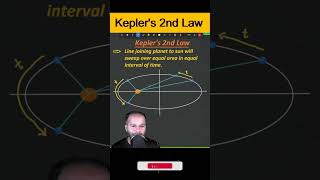
Moving on to Kepler's Second Law: it states that the line joining a planet and the Sun sweeps out equal areas in equal time intervals. Why might this be important?
Could it help us understand the speed of the planets?
Exactly! This law reveals that as a planet gets closer to the Sun, it moves faster. It conserves angular momentum, meaning when it's near the Sun, the planet travels more distance in the same timeframe. Let's visualize: if we look at a planet's orbital path, it covers a larger area when close to the Sun compared to when it's farther away. Can you think of an example?
Mars moves faster at perihelion compared to aphelion!
Correct! To reinforce this concept, remember: 'Speed up when close!' Finally, can anyone summarize what Kepler's Second Law tells us?
It shows that planets cover more area faster when they are nearer to the Sun.
Kepler's Third Law
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
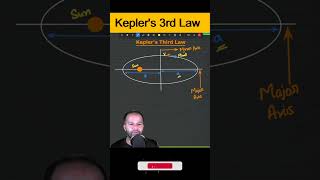
Let’s dive into Kepler's Third Law. We're learning that the square of the orbital period is proportional to the cube of the semi-major axis. What does that mean for the planets?
Does it mean that the farther a planet is from the Sun, the longer its orbit takes?
You got it! For example, if we know that Earth takes one year to orbit the Sun, we can calculate that distant planets take even longer. Let's put this formula into practice: T² ∝ a³. How does this play out for Jupiter and Earth?
Jupiter takes 11.9 Earth years; its semi-major axis is much larger!
Exactly! For practice, think of the ratio for all planets: T²/a³ should be constant. This relationship is crucial for predicting planetary movements. Now, summarize this law’s importance.
Kepler’s Third Law helps us predict how long planets take to orbit based on their distance from the Sun.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Kepler's three laws of planetary motion detail the elliptical shapes of planetary orbits with the Sun at one focus, the equal area swept over equal time intervals, and how a planet's orbital period squared is proportional to the cube of its average distance from the Sun. These laws laid the foundation for Newton's law of gravitation.
Detailed
Detailed Summary of Kepler's Laws
Johannes Kepler formulated three fundamental laws of planetary motion in the early 17th century, which significantly contributed to our understanding of celestial mechanics.
1. Kepler's First Law (Law of Orbits)
All planets move in elliptical orbits with the Sun situated at one of the foci of the ellipse. This was a departure from the earlier belief in circular orbits. The concept of an ellipse can be simply illustrated by fixing two points (foci) and tracing a curve with a taut string. The points of closest approach and farthest distance from the Sun are called the perihelion and aphelion, respectively.
2. Kepler's Second Law (Law of Areas)
The line segment joining a planet to the Sun sweeps out equal areas in equal time intervals. This dynamic implies that a planet moves faster when it is closer to the Sun and slower when it is farther from it. This law can be understood through the conservation of angular momentum.
3. Kepler's Third Law (Law of Periods)
The square of the orbital period (T) of a planet is proportional to the cube of the semi-major axis (a) of its orbit. This relationship can be mathematically expressed as T² ∝ a³. A table of planetary motions supports the accuracy of this law, demonstrating that the ratio of T² to a³ is consistent across the solar system.
Kepler's laws not only provided a detailed description of how planets move but also served as a critical stepping stone for Newton, who later articulated the universal law of gravitation.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Kepler's First Law: Law of Orbits
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Law of Orbits: All planets move in elliptical orbits with the Sun situated at one of the foci.
Fig. 7.1(a) An ellipse traced out by a planet around the sun. The closest point is P and the farthest point is A. P is called the perihelion and A the aphelion. The semimajor axis is half the distance AP.
Fig. 7.1(b) Drawing an ellipse. A string has its ends fixed at F1 and F2. The tip of a pencil holds the string taut and is moved around.
Detailed Explanation
Kepler's First Law states that planets do not travel in perfect circles around the Sun, but rather in elliptical orbits. An ellipse is a shape that is elongated in two directions with two focal points. In this law, one focus is occupied by the Sun. The distance between the closest point of the planet to the Sun (the perihelion) and the farthest point (the aphelion) varies. This law helps us understand that a planet's distance from the Sun changes as it orbits, which was a significant advancement over earlier models that assumed circular orbits.
To visualize an ellipse, you can use a method involving a string: fix two points (the foci) and keep the string taut while moving a pencil around. This creates an oval shape - the ellipse. Importantly, for any point on the ellipse, the total distance from the two foci is constant.
Examples & Analogies
Think of a basketball and a bowling ball. If you roll the bowling ball in a straight line, it moves in a straight path (like a circular orbit). However, when you roll the basketball in a slightly squished path (like an ellipse), it resembles how planets orbit the Sun, where they are sometimes closer and sometimes further from it.
Kepler's Second Law: Law of Areas
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Law of Areas: The line that joins any planet to the sun sweeps equal areas in equal intervals of time.
Fig. 7.2 The planet P moves around the sun in an elliptical orbit. The shaded area is the area ΔA swept out in a small interval of time Δt.
Detailed Explanation
Kepler's Second Law, also known as the Law of Areas, emphasizes that a planet travels faster when it is closer to the Sun and slower when it is farther away. The area covered by the line drawn from the Sun to the planet in a specific time remains constant, regardless of where the planet is in its orbit. This conclusion is derived from the conservation of angular momentum. When a planet speeds up as it approaches perihelion, it sweeps out a larger area in a shorter time, compensating for the slower movement when it is at aphelion, ensuring the area swept remains consistent across equal time intervals.
Examples & Analogies
Think of a swing on a playground. When you pull it back and let it go, it swings faster when it's close to you and slows down at the top of its arc farthest from you. Similarly, planets speed up and slow down as they orbit the Sun, but the areas they cover in equal intervals of time remain constant.
Kepler's Third Law: Law of Periods
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Law of Periods: The square of the time period of revolution of a planet is proportional to the cube of the semi-major axis of the ellipse traced out by the planet.
Table 7.1 provides the approximate time periods of revolution of eight planets around the sun along with values of their semi-major axes.
Detailed Explanation
Kepler's Third Law relates the time it takes for a planet to complete an orbit (its period) to its average distance from the Sun (the semi-major axis). Specifically, the square of a planet's orbital period (T²) is proportional to the cube of its average distance from the Sun (a³). This means if you know the distance of a planet from the Sun, you can predict its orbital period. This relationship is mathematically represented as T² ∝ a³. Kepler's observations confirmed that this relationship holds true across all planets in the solar system.
Examples & Analogies
Imagine planets are dancers in a solar ballet. The farther a dancer is from the center stage (the Sun), the slower they move around it. If you're standing at the edge of a dance floor, you would have to take longer to complete a lap around the center than if you were dancing right next to it. This illustrates how distance affects movement and time in orbiting paths.
Understanding the Law of Areas through Angular Momentum
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The law of areas can be understood as a consequence of conservation of angular momentum, which is valid for any central force. A central force is such that the force on the planet is along the vector joining the Sun and the planet.
Detailed Explanation
The conservation of angular momentum states that in the absence of external torques, the total angular momentum of a system remains constant. In the context of planets and the Sun, as a planet moves closer to the Sun, it speeds up and as it moves away, it slows down. This balancing act ensures that the area swept out is constant over equal time intervals. Since gravitational force from the Sun acts along the radius connecting planet and Sun, it behaves as a central force, making angular momentum conservation applicable and demonstrating why Kepler's second law holds true.
Examples & Analogies
Think of a spinning figure skater. When they pull their arms in close to their body, they spin faster. Conversely, when they extend their arms, they slow down. Similarly, as planets change their distance from the Sun, they adjust their speed while conserving their angular momentum.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
First Law: Planets move in elliptical orbits with the Sun at one focus.
-
Second Law: A line segment joining a planet to the Sun sweeps out equal areas during equal time intervals.
-
Third Law: The square of the orbital period of a planet is proportional to the cube of the semi-major axis of its orbit.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An example of Kepler's First Law: The orbit of Earth around the Sun is an ellipse with the Sun at one focus.
-
For Kepler's Second Law, Mars moves faster when it's closer to the Sun at perihelion than when it's at aphelion.
-
According to Kepler's Third Law, if Earth takes 1 year to orbit the Sun, a planet with a semi-major axis 2 times larger will take about 2.83 years.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Ellipses are the shape we see, paths of planets flying free.
📖 Fascinating Stories
-
Imagine a planet racing close to the Sun, speeding up its journey, having so much fun!
🧠 Other Memory Gems
-
E – Ellipse, Area – Equal, Period – Proportional (EAP).
🎯 Super Acronyms
FAP - First law (Focus), Area (Second Law), Proportional (Third Law).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Elliptical Orbit
Definition:
An orbit in the shape of an ellipse, a flattened circle.
-
Term: Perihelion
Definition:
The closest point in the orbit of a planet to the Sun.
-
Term: Aphelion
Definition:
The farthest point in the orbit of a planet from the Sun.
-
Term: Angular Momentum
Definition:
The rotational equivalent of linear momentum, conserved in orbital systems.
-
Term: SemiMajor Axis
Definition:
Half of the longest diameter of an ellipse, important in defining the size of an orbit.