Learn
Games

7.3 - UNIVERSAL LAW OF GRAVITATION

Interactive Audio Lesson

Listen to a student-teacher conversation explaining the topic in a relatable way.

Introduction to Universal Law of Gravitation

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Welcome class! Today we are going to discuss one of the most significant laws in physics - the Universal Law of Gravitation. Can anyone tell me what they think this law involves?

Student 1
Student 1

Is it about why things fall to the ground?

Teacher
Teacher

Exactly! This law explains that every mass attracts every other mass. Does anyone know how this force is calculated?

Student 2
Student 2

I think there's a formula for it?

Teacher
Teacher

Correct! The formula is F = G * (m1 * m2) / r². Here, G is the gravitational constant. Remember this formula by using the acronym FRIEND: Force = (Gravitational Constant) x (Mass1 x Mass2) / (Distance squared).

Understanding Gravitational Force

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Now let's delve deeper into the factors affecting the gravitational force. Can anyone list some of these factors?

Student 3
Student 3

I guess the masses of the two objects and the distance between them?

Teacher
Teacher

Exactly! The gravitational force increases with the mass of the objects and decreases with the square of the distance between them. Remember this with the mnemonic 'Mass Matters, Distance Diminishes.' Can anyone explain why distance decreases the force?

Student 4
Student 4

Because the further apart they are, the weaker the pull?

Teacher
Teacher

That's right! This is crucial for understanding how planets orbit. They don’t just 'fall' into each other due to their vast distances.

Applications of the Universal Law of Gravitation

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

The Universal Law of Gravitation is fundamental in understanding celestial mechanics. How does this law relate to objects in orbits, such as satellites or planets?

Student 1
Student 1

Does it mean that the gravitational force keeps these objects in orbit?

Teacher
Teacher

Exactly! The gravitational pull from larger bodies like the Earth keeps satellites in orbit. It’s a balance between the gravitational force pulling inward and the object's velocity trying to move away. Anyone can explain the importance of this balance?

Student 2
Student 2

If the speed is too high, the object could escape the gravitational pull?

Teacher
Teacher

Correct! This is why we have escape velocity. It's fascinating how these concepts are interconnected! Remember: Gravity not only pulls but defines paths of movement in our universe.

Introduction & Overview

Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.

Quick Overview

The Universal Law of Gravitation explains the gravitational attraction between two masses and forms the foundation for understanding orbits in celestial mechanics.

Standard

Isaac Newton's Universal Law of Gravitation states that every particle attracts every other particle in the universe with a force proportional to the product of their masses and inversely proportional to the square of the distance between them. This law plays a crucial role in explaining gravitational phenomena and the motion of celestial bodies.

Detailed

Universal Law of Gravitation

Newton's Universal Law of Gravitation postulates that every mass in the universe attracts every other mass with a force that is:
- Directly proportional to the product of their masses
- Inversely proportional to the square of the distance between their centers.

Mathematically, this is represented as:

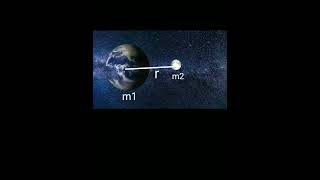
F = G * (m1 * m2) / r^2

where
- F is the gravitational force between two objects,
- m1 and m2 are the masses of the objects,
- r is the distance between their centers, and
- G is the universal gravitational constant (approximately 6.67 × 10^-11 N m²/kg²).

This fundamental law explains not only the motion of objects on Earth but also the orbits of celestial bodies and the behavior of planets in relation to one another. It illustrates the concept that gravitational forces decrease with distance, and it forms the basis for further developments in gravitational theory, including concepts like gravitational potential energy and orbital mechanics.

Youtube Videos

Newtons Law Of Gravitation Definition - A Level Physics
Newtons Law Of Gravitation Definition - A Level Physics
The Universal Law of Gravitation - Part 1 | Physics | Don't Memorise
The Universal Law of Gravitation - Part 1 | Physics | Don't Memorise
Gravitation Class 11 Physics Chapter 8 - Universal Law of Gravitation
Gravitation Class 11 Physics Chapter 8 - Universal Law of Gravitation
Understanding Universal law of Gravitation!
Understanding Universal law of Gravitation!
Work and Energy Class One shot 🔥| All Important Topics | Class 9th Science | NCERT | Part 3
Work and Energy Class One shot 🔥| All Important Topics | Class 9th Science | NCERT | Part 3
Universal law of gravitation #gravity
Universal law of gravitation #gravity
Newton aur Gravity ki Kahani | Newton's law of Gravitation | Tushar Patel Physics Expert | Embibe
Newton aur Gravity ki Kahani | Newton's law of Gravitation | Tushar Patel Physics Expert | Embibe
Newton's Law of Universal Gravitation
Newton's Law of Universal Gravitation

Audio Book

Dive deep into the subject with an immersive audiobook experience.

Inspiration of Newton

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Legend has it that observing an apple falling from a tree, Newton was inspired to arrive at an universal law of gravitation that led to an explanation of terrestrial gravitation as well as of Kepler’s laws.

Detailed Explanation

This chunk introduces the motivation behind Newton's formulation of the Universal Law of Gravitation. The story of an apple falling provides a simple imagery that sparks curiosity about gravity. Newton observed natural phenomena and connected them to a larger principle governing all matter in the universe.

Examples & Analogies

Imagine dropping a ball from a certain height. Just like Newton thought about why the apple fell straight down, we can think about why the ball hits the ground instead of floating away. Both the apple and the ball are affected by the force of gravity, which acts on objects regardless of their mass.

Centripetal Acceleration of the Moon

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Newton’s reasoning was that the moon revolving in an orbit of radius Rm was subject to a centripetal acceleration due to earth’s gravity of magnitude a = V²/Rm, where V is the speed of the moon related to the time period T by the relation V = 2πRm/T.

Detailed Explanation

Here, Newton explains a key concept of centripetal acceleration, which is the acceleration needed to keep an object moving in a circular path. The moon, while orbiting the Earth, experiences this acceleration due to gravitational pull. The two equations show the relationship between the moon's speed, the radius of its orbit, and the time period of the orbit.

Examples & Analogies

Think of riding a merry-go-round. To stay on a circular path, you need to lean inward because of the force acting towards the center. Similarly, the moon 'leans' towards Earth as it travels along its path, demonstrating how gravity keeps it in orbit.

Inverse Square Law of Gravity

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

If one assumes that the gravitational force due to the earth decreases in proportion to the inverse square of the distance from the centre of the earth, we will have a = g / R².

Detailed Explanation

This statement describes the inverse square law, foundational to gravitational theory. It means as the distance from Earth increases, the gravitational force decreases rapidly. This principle explains why objects farther away from Earth, like satellites far in orbit, experience less gravitational influence compared to objects closer to Earth.

Examples & Analogies

Imagine blowing up a balloon. The air inside is pushed uniformly, but the pressure felt at the surface (like gravity) diminishes as you move away from the center. Similarly, the farther you get from the Earth, the weaker the gravitational force becomes.

Statement of the Universal Law

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

These observations led Newton to propose the following Universal Law of Gravitation: Every body in the universe attracts every other body with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.

Detailed Explanation

This statement summarizes the Universal Law of Gravitation. It articulates how every mass attracts every other mass with a certain force, which can be calculated using Newton's formula. This law allows us to understand and calculate the gravitational interaction between any two objects in the universe, playing a fundamental role in celestial mechanics.

Examples & Analogies

Consider two friends on a playground. If one friend holds a large ball while the other holds a small ball, the gravitational pull is stronger between the large ball and the larger friend nearby. However, as the two friends move apart, the effect of their attraction diminishes significantly, demonstrating how gravitational forces work in relation to mass and distance.

Mathematical Expression of Gravity

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Stated Mathematically, Newton’s gravitation law reads: F = G(m1*m2)/r², where G is the universal gravitational constant.

Detailed Explanation

This chunk provides the mathematical foundation of Newton's Law of Gravitation. The expression indicates how gravitational force (F) is calculated based on the masses of two objects (m1 and m2) and the distance (r) between their centers. G, the gravitational constant, is a key component that provides the necessary value for gravity based on the units used.

Examples & Analogies

Think of it like a recipe for a cake. To bake a cake, you need certain quantities of flour (mass 1) and sugar (mass 2) and mix them together at a specific ratio (distance) to create a tasty treat (gravitational force). The constant G is like the oven temperature: it determines how well the ingredients come together to bake successfully.

Vector Form of Gravitational Force

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

The force on point mass m1 due to another point mass m2 has the magnitude F12 = - F21, showcasing Newton's third law.

Detailed Explanation

This part expands on the idea that forces are mutual. The force that one mass exerts on another is equal in magnitude and opposite in direction to the force exerted back. This mutual attraction is at the heart of gravitational interactions and illustrates the concept of action and reaction as stated in Newton's third law.

Examples & Analogies

Imagine two people pushing against each other. Both exert equal effort in opposite directions. Just as they feel the force they apply, so do the bodies in the universe feel the gravitational pulls of one another, reflecting the balance of forces all around.

Force on Extended Objects

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Before we can apply Eq. (7.5) to objects under consideration, we have to be careful since the law refers to point masses whereas we deal with extended objects which have finite size.

Detailed Explanation

This chunk emphasizes that while Newton's law applies to point masses, real objects have volume and spread out the gravitational force across their entire mass. The gravitational influence of larger bodies must be calculated considering distribution of mass, often through calculus.

Examples & Analogies

Think of a crowd of people. If you ask a group of people (the mass) to pull on a large rope (the gravitational force), it's important to consider how they are distributed along the rope's length. All exert some force, but their combined effort can differ based on their arrangement and distances from each other.

Definitions & Key Concepts

Learn essential terms and foundational ideas that form the basis of the topic.

Key Concepts

  • Attraction between masses: Every mass attracts every other mass directly proportional to their product.

  • Force equation: F = G * (m1 * m2) / r² describes gravitational force.

  • Distance effect: Gravitational force decreases with the square of the distance.

  • Escape Velocity: The minimum speed required to overcome Earth's gravitational pull.

Examples & Real-Life Applications

See how the concepts apply in real-world scenarios to understand their practical implications.

Examples

  • The gravitational force between two spheres can be calculated using their masses and the distance between their centers.

  • Satellites remain in orbit around Earth due to the balance between their speed and the gravitational pull of Earth.

Memory Aids

Use mnemonics, acronyms, or visual cues to help remember key information more easily.

🎵 Rhymes Time

  • Attraction is the game, between masses they claim; the more you weigh, the stronger the pull—distance is the rule, so keep it cool!

📖 Fascinating Stories

  • Imagine an adventurous astronaut who discovers that his spaceship is attracted to planets not only because of their size but also how far he is from them. The closer he gets, the stronger the pull!

🧠 Other Memory Gems

  • To remember the formula: 'Frogs Grow Massively (G) when they’re Underwater (U)'; (F = G * (m1 * m2) / r²)

🎯 Super Acronyms

To recall the components of gravitational interaction, think 'Mighty Ducks' - Mass (M), Distance (D), Force (F).

Flash Cards

Review key concepts with flashcards.

Glossary of Terms

Review the Definitions for terms.

  • Term: Universal Law of Gravitation

    Definition:

    A law stating that every mass attracts every other mass with a force that is proportional to their masses and inversely proportional to the square of the distance between them.

  • Term: Gravitational Constant (G)

    Definition:

    A constant that represents the strength of the gravitational force in the equation of gravitation, valued at approximately 6.67 × 10^-11 N m²/kg².

  • Term: Centripetal Force

    Definition:

    The force required to keep an object moving in a circular path, directed towards the center of that path.

  • Term: Escape Velocity

    Definition:

    The minimum speed required for an object to break free from the gravitational attraction of a celestial body.