Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Progressive Waves
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will discuss progressive waves and how their displacement can be mathematically represented. Does anyone know what a progressive wave is?
Isn't it a wave that moves through a medium?
Correct! Progressive waves transport energy through a medium, and each particle of the medium oscillates around its equilibrium position. Let's look at the mathematical representation of such a wave.
Do we have a specific equation for that?
Yes, a sinusoidal traveling wave can be represented as y(x,t) = a sin(kx - Οt + Ο). Here, 'y' is the displacement, 'x' is the position, 't' is time, 'a' is the amplitude, and 'k' and 'Ο' represent the wave's angular parameters. Let's break down these components further.
Understanding Amplitude and Phase
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
In our wave function, 'a' represents amplitude, which is the maximum displacement from equilibrium. Can someone tell me what we mean by phase?
I think it's related to how far along the wave is at a given time.
Exactly, the phase affects the position of the wave at any point in time. A phase shift can change how the wave appears without altering its amplitude or frequency.
So if I change the phase, I just shift the wave left or right?
Correct! This concept is crucial in understanding how waves interact when they overlap.
Wavelength and Speed of a Wave
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, letβs talk about wavelength. Itβs the distance between two points on the wave that are in phase.
Are there specific points we should identify for that?
Good question! Typically, we look at crests or troughs as these points. How do we relate the wavelength with frequency and speed?
I remember the speed formula! Speed equals wavelength times frequency, right?
Exactly! The formula v = fΞ» shows how speed, frequency, and wavelength are intertwined. Understanding this relationship is foundational for analyzing wave phenomena.
Deriving Wave Properties
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we know the key terms, letβs derive some wave properties using the equation. Can someone summarize what the variables represent again?
We have amplitude 'a', wave number 'k', angular frequency 'Ο', and the phase 'Ο'.
Right! Those components lead to understanding vibrations and oscillations of each particle in the medium. Who can explain how they would visualize solving for the speed?
We could set relations between frequency and angular frequency!
Exactly! Let's practice deriving these relationships based on the properties we've discussed.
Recap of Key Concepts
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
So as we conclude, what are the key takeaways we discussed today?
We learned how to represent waves mathematically with the function y(x, t).
And the importance of amplitude and phase in defining their behavior!
Exactly! Remember, knowing how these properties work together enables us to predict wave behavior. Be sure to review these concepts as we progress!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the displacement relation of a sinusoidal traveling wave, characterized by its amplitude, wavelength, frequency, and phase. We derive the functions that describe the wave's propagation and define key terms such as amplitude, phase, wavelength, and frequency, emphasizing their significance.
Detailed
In the study of waves, understanding the displacement relation in a progressive wave is vital to grasping how these waves propagate through a medium. This section begins by describing a sinusoidal traveling wave mathematically using the function y(x, t) = a sin(kx - Οt + Ο), where 'y' represents displacement, 'x' position, 't' time, 'a' amplitude, 'k' angular wave number, 'Ο' angular frequency, and 'Ο' phase constant.
The equation illustrates how the wave's shape changes over time and space while maintaining its sinusoidal nature. By setting Ο to zero, we simplify our understanding, making the wave's mathematical analysis more manageable. We delve into the concepts of amplitude β the maximum displacement from equilibrium β and phase, which determines the position of the wave at any point.
Moreover, we define wavelength as the distance between two consecutive points in phase, and relate the angular frequency and wave characteristics to their respective equations, including T (period), frequency, and speed of the wave. This mathematical framework provides crucial foundations for further exploration of wave behavior, including transmission, interference, and harmonic patterns.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Mathematical Description of a Travelling Wave
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For mathematical description of a travelling wave, we need a function of both position x and time t. Such a function at every instant should give the shape of the wave at that instant. Also, at every given location, it should describe the motion of the constituent of the medium at that location. If we wish to describe a sinusoidal travelling wave the corresponding function must also be sinusoidal.
Detailed Explanation
To mathematically describe a travelling wave, we need to create a formula that changes over time and position. This means for any specific moment in time (t) and at any specific location (x), the formula should represent the wave's shape and the movements of the particles in that medium. If the wave is sinusoidal, implying a smooth, repetitive oscillation, the mathematical representation must also take the sinusoidal form.
Examples & Analogies
Think of a sinusoidal wave as a smooth rippling effect when you drop a stone into a calm pond. At different points in the pond, the water level rises and falls in a sinusoidal pattern, creating ripples which can be mathematically described with sinusoidal functions.
Sinusoidal Wave Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A sinusoidal travelling wave is then described by: ( , ) sin( )= βΟ +Οy xt a kx t (14.2)
Detailed Explanation
The equation for a sinusoidal travelling wave is given as y(x,t) = a sin(kx - Οt + Ο). Here, 'y' represents the displacement of the wave at any position and time, 'a' is the amplitude (the maximum displacement), 'k' is the wave number (related to wavelength), 'Ο' is the angular frequency (related to how fast the wave oscillates), and 'Ο' is the phase constant (determining the wave's position at time t=0). Each of these components plays a crucial role in shaping the wave's behavior.
Examples & Analogies
Imagine you're pulling a long rope up and down to create waves. The pull (amplitude) determines the height (maximum displacement). How quickly you pull it back and forth (angular frequency) changes how many waves you can create in a given time. The position of your hand when the rope is at rest (phase) determines where the wave starts its journey.
Understanding Wave Behavior Over Time
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To understand why represents a sinusoidal travelling wave, take a fixed instant, say t = t0. Then, the argument of the sine function is simply kx + constant.
Detailed Explanation
When we analyze the equation further, if we set a specific time (let's say t = t0), the equation simplifies to show how the wave's shape varies based on position x. This means that whether we hold time constant or fix our location, we are able to see how the wave oscillates and moves forward. This relationship gives us valuable insights into wave characteristics, such as how it displaces the medium at different points.
Examples & Analogies
If you've ever recorded a wave's pattern at a water surface, you can relate the height of the wave (displacement) to how far you are from where the stone was dropped (position) at that specific time you took the recording. You would note that as time progresses and you keep 'drawing' the surface, the wave pattern reveals both the ripples (shape) and the locations further from the drop point.
Amplitude and Phase of the Wave
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
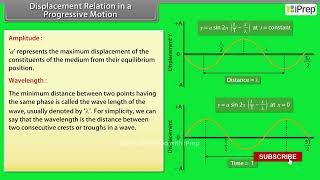
since the sine function varies between 1 and β1, the displacement y (x,t) varies between a and β a. We can take a to be a positive constant, without any loss of generality. Then, a represents the maximum displacement of the constituents of the medium from their equilibrium position. Note that the displacement y may be positive or negative, but a is positive. It is called the amplitude of the wave.
Detailed Explanation
The amplitude (a) indicates the peak value of displacement from the wave's central position (equilibrium). Since the sine function's output ranges from -1 to 1, the wave's displacement can move between its maximum positive (a) and maximum negative (-a) values. This shows how far particles of the medium move up and down as the wave travels.
Examples & Analogies
Consider a child on a swing. The highest point they reach above ground level represents the amplitude. Whether they are swinging up (positive displacement) or down (negative displacement), the highest points are consistent, showing how far they swing out from the center.
Phase and Its Importance
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The quantity ( kx β Οt + Ο) appearing as the argument of the sine function is called the phase of the wave.
Detailed Explanation
The phase (kx - Οt + Ο) determines the specific position of the wave at any point in time. By understanding the phase relationship, we can know when and where the wave has maximum displacement, and it helps us track wave motion over time. It essentially captures the timing of the wave's cycle.
Examples & Analogies
Think of the phase like the current time showing when a song plays. Depending on where you are at in the song (the phase), the melody changes. If you come in at different parts, you're experiencing different notes just as different phases of a wave represent different positions in its oscillation.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Wave Function: The mathematical description of a wave's displacement as a function of position and time.
-
Amplitude: The maximum extent of a vibration or oscillation from a zero point.
-
Phase: The angle describing the state of the wave at a point in time and space.
-
Wavelength: The distance between consecutive points of equivalent phase in a wave.
-
Angular Frequency: A measure of how quickly the wave oscillates in radians per unit time.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The equation y(x, t)=3 sin(2x - 4t) represents a wave with an amplitude of 3, angular frequency of 4 rad/s, and wavelength given by 2Ο/k.
-
In sound waves, the length of the air column can dictate wave characteristics, including speed and frequency, as explained by the wave equation.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Away the wave goes, through the air it flows, amplitude high, as the energy grows!
π Fascinating Stories
-
Once in a cosmic sea, waves danced in delight, their peaks high with amplitude, shining bright with light.
π§ Other Memory Gems
-
A.P.W.F. for remembering wave aspects: Amplitude, Phase, Wavelength, Frequency.
π― Super Acronyms
WAVE - Wavelength, Amplitude, Velocity, Energy.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Amplitude
Definition:
The maximum displacement of a particle from its equilibrium position in a wave.
-
Term: Phase
Definition:
A measure of the position of a wave relative to a reference point at a specific time.
-
Term: Wavelength
Definition:
The distance between two successive points of the same phase along a wave.
-
Term: Angular Frequency
Definition:
The rate of oscillation of a wave, measured in radians per second, often symbolized as Ο.
-
Term: Wave Number
Definition:
The spatial frequency of a wave, defined as the number of wavelengths per unit distance, symbolized as k.