Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Superposition
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we are going to learn about the principle of superposition of waves. This principle helps us understand how waves interact with one another as they travel through a medium.
What exactly is the principle of superposition?
Great question! The principle states that when two or more waves overlap, the total displacement of the medium at any point is the sum of the individual displacements caused by each wave.
So, they can add up? What happens if they cancel each other?
Yes, thatβs correct! This can happen through constructive and destructive interference. Constructive occurs when waves add together, and destructive occurs when they cancel each other out.
Is there a real-world example of this?
Absolutely, when you hear two musical notes played together, the variations in loudness you perceive are results of the interference of sound waves. That's an application of the principle of superposition!
Remember, the key here is that each wave maintains its identity while overlapping. This understanding is essential for deeper wave phenomena, leading into concepts like beats and standing waves.
Mathematics of Superposition
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Next, letβs delve into the mathematics of superposition. If wave disturbances in a media are given by functions y1 and y2, the resulting wave can be described mathematically.
Can you show us how that looks?
Certainly! The total displacement at any point is given by: `y(x,t) = y1(x,t) + y2(x,t)`.
What does `y1` and `y2` represent?
`y1` and `y2` represent the displacements due to the individual waves. This additive property is crucial for analyzing wave interactions.
How does this help us understand interference patterns?
By understanding how the waves add together or cancel out, we can explain phenomena like beats, where we perceive variations in sound intensity due to close frequencies.
In essence, superposition provides the foundation for analyzing complex wave systems by simplifying them into manageable equations.
Applications of Superposition
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's explore some applications of the principle of superposition. It plays a vital role in various fields, such as acoustics and optics.
Could you give an example in acoustics?
Sure! When two instruments play the same note slightly out of tune, we hear beats. The interference of sound waves results in fluctuating loudness.
What about in optics?
In optics, superposition helps explain interference patterns in films, such as soap bubbles, where different wavelengths create colorful patterns due to wave addition.
So, it seems superposition is everywhere!
Exactly! Understanding this principle enables us to analyze any wave phenomena, allowing engineers and scientists to innovate in technology like sound systems and optical equipment.
Remember, recognizing how waves interact creates a pathway to many advanced topics, including quantum mechanics and beyond.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the principle of superposition of waves, illustrating how overlapping wave pulses change the resultant wave's shape without altering the individual wave's propagation. This fundamental principle underlies many wave phenomena such as interference.
Detailed
The Principle of Superposition of Waves
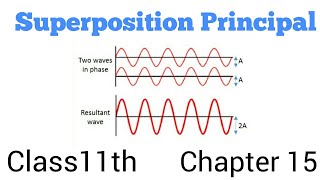
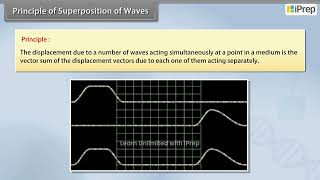
The principle of superposition asserts that when two wave pulses travel through the same medium and overlap, the total displacement of the medium at any point is the sum of the displacements due to the individual waves. This principle allows us to analyze complex wave interactions by breaking them down into simpler components.
Key Concepts:
- Wave Overlap: When two wave pulses meet, their individual characteristics remain unchanged after the overlap.
- Resultant Displacement: The combined displacement is calculated as the algebraic sum of the displacements from the individual waves.
- Constructive and Destructive Interference: When waves meet in phase (constructive), their amplitudes add; when out of phase (destructive), they can cancel each other out completely.
Mathematically, for two overlapping waves with displacements represented as y1(x,t) and y2(x,t), the net displacement y(x,t) is given by:
$$y(x,t) = y_1(x,t) + y_2(x,t)$$
This principle forms the basis for interference patterns and standing waves. Understanding superposition is crucial for comprehending various physical phenomena, including sound, light, and electromagnetic waves.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Superposition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
What happens when two wave pulses travelling in opposite directions cross each other? It turns out that wave pulses continue to retain their identities after they have crossed. However, during the time they overlap, the wave pattern is different from either of the pulses.
Detailed Explanation
When two waves move towards each other and overlap, each wave maintains its individual characteristics, even while they intersect. This means that instead of blending into one indistinct wave, each pulse retains its identity after crossing. However, when they are overlapping, their effect on the medium is combined, creating a new displacement pattern during that moment. This phenomenon illustrates how waves can coexist and influence the medium in which they travel without permanently altering each other's states.
Examples & Analogies
Imagine two people walking towards each other in a crowded hall. As they pass each other, they donβt meld into one person; rather, they intersect and continue on their paths. Similarly, the wave pulses maintain their distinct forms even while they temporarily affect each other.
Algebraic Sum of Displacements
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When the pulses overlap, the resultant displacement is the algebraic sum of the displacement due to each pulse. This is known as the principle of superposition of waves.
Detailed Explanation
The principle of superposition states that when two or more waves overlap in a medium, the total displacement at any point is the sum of the individual displacements from each wave. This means that if one wave displaces the medium in one direction and another displaces it in the opposite direction, the net displacement can be calculated by simply adding the values (considering the directions). This can lead to scenarios where they amplify each other (constructive interference) or cancel each other out (destructive interference).
Examples & Analogies
Think of two musicians playing different notes. When they play together, the sound combines in a way that can either enhance the music (when the notes harmonize) or cancel each other out (when the notes clash). The resulting sound is like the resulting displacement of the waves.
Mathematical Representation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To put the principle of superposition mathematically, let y1 (x,t) and y2 (x,t) be the displacements due to two wave disturbances in the medium. If the waves arrive in a region simultaneously, and therefore, overlap, the net displacement y (x,t) is given by y (x, t) = y1(x, t) + y2(x, t).
Detailed Explanation
In a mathematical context, we can represent the displacements caused by two different waves as y1 and y2. When these waves coincide at the same point in space and at the same time, their combined effect, or resultant displacement, y, is simply the sum of the individual displacements. This algebraic sum highlights how the characteristics of waves can superimpose, affecting the resultant wave form in a predictable manner.
Examples & Analogies
Imagine two rivers merging into one. Each river maintains its own current and water characteristics, but together they create a broader flow of water. The combined flow at any point where the two meet is comparable to the sum of the individual contributions of both rivers, just as the waves combine their displacements.
Multiple Wave Interactions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If we have two or more waves moving in the medium the resultant waveform is the sum of wave functions of individual waves.
Detailed Explanation
In scenarios where more than two waves are interacting, the principle of superposition extends beyond just two waves. The total displacement at any point in the medium is the cumulative sum of all individual wave functions. This gives rise to complex wave patterns that can change dynamically, depending on the number of waves and their respective amplitudes, frequencies, and phases.
Examples & Analogies
Consider a large concert with multiple instruments playing together. Each musician contributes their unique sound, and altogether they create a complex piece of music. Similarly, multiple waves interacting create intricate patterns resulting from their combined effects.
Resultant Waveforms and Interference
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The significant thing is that its amplitude is a function of the phase difference Ο between the constituent two waves.
Detailed Explanation
The resulting wave formed by the superposition of two waves also depends on the phase difference between them. If the waves are in phase (i.e., their peaks and troughs line up), they can combine to create a wave with greater amplitude (constructive interference). Conversely, if they are completely out of phase (the peak of one coincides with the trough of another), they can cancel each other out (destructive interference). This relationship between phase difference and amplitude is crucial in understanding wave behavior in many physical systems.
Examples & Analogies
Think about pushing two children on swings. If you push both at the same time while they are in sync, they swing higher and faster together. However, if one swing goes up when the other goes down, they might not get very high at all. This illustrates constructive and destructive interference based on how synchronized their movements are.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Wave Overlap: When two wave pulses meet, their individual characteristics remain unchanged after the overlap.
-
Resultant Displacement: The combined displacement is calculated as the algebraic sum of the displacements from the individual waves.
-
Constructive and Destructive Interference: When waves meet in phase (constructive), their amplitudes add; when out of phase (destructive), they can cancel each other out completely.
-
Mathematically, for two overlapping waves with displacements represented as
y1(x,t)andy2(x,t), the net displacementy(x,t)is given by: -
$$y(x,t) = y_1(x,t) + y_2(x,t)$$
-
This principle forms the basis for interference patterns and standing waves. Understanding superposition is crucial for comprehending various physical phenomena, including sound, light, and electromagnetic waves.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of two sound waves from musical instruments interfering to create beats.
-
Visualizing overlapping water waves in a pond during a rainstorm demonstrating superposition.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
When waves collide, they'll multiply; overlapping peaks will touch the sky.
π Fascinating Stories
-
Imagine two rivers meeting, flowing together, the waters combine or sometimes flow silently past each other, precisely illustrating how waves superimpose.
π§ Other Memory Gems
-
Crispy Cereal (Constructive = Combine) and Diminished Dumplings (Destructive = Diminish) help remember types of interference.
π― Super Acronyms
WAVE
- Waves Add
- versus Waves Eliminate β remembering superposition effects.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Superposition
Definition:
The principle that when two or more waves overlap, the resultant displacement is the algebraic sum of the individual displacements.
-
Term: Constructive Interference
Definition:
When two waves coincide in phase, resulting in a larger amplitude.
-
Term: Destructive Interference
Definition:
When two waves are out of phase, causing them to cancel each other out.
-
Term: Wave Pulse
Definition:
A single disturbance that travels through a medium, characterized by a specific shape or form.
-
Term: Resultant Wave
Definition:
The wave produced from the superposition of two or more waves.