Learn
Games

12.2.2 - Factorisation by regrouping terms

Interactive Audio Lesson

Listen to a student-teacher conversation explaining the topic in a relatable way.

Introduction to Factorisation by Regrouping

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Today, we are going to explore an interesting way to factor expressions called 'factorisation by regrouping'. Can anyone explain what they think that means?

Student 1
Student 1

Is it like finding common factors in an expression?

Teacher
Teacher

Yes, exactly! It's about reorganizing terms to find those common factors. For example, in the expression 2xy + 2y + 3x + 3, if we group the first two and the last two terms, we can see something interesting.

Student 2
Student 2

What do you see when you group them?

Teacher
Teacher

The first two terms can be factored as 2y(x + 1) and the last two as 3(x + 1). So we can rewrite the whole expression as (x + 1)(2y + 3).

Student 3
Student 3

I see! That helps a lot! So we rearranged to find common factors.

Teacher
Teacher

Exactly! Let's remember: 'Group to find.' If you can identify groups that can simplify an expression, you'll unveil common factors!

Practical Example of Regrouping

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Consider the expression 6xy - 4y + 6 - 9x. Can anyone identify potential groups here?

Student 2
Student 2

Maybe we can group 6xy with -9x and -4y with 6?

Teacher
Teacher

Great observation! Let's try that. If we rearrange it as 6xy - 9x - 4y + 6, we can factor the first group as 3(3y - 2) and the second group as -1(3y - 2).

Student 1
Student 1

So we can factor out (3y - 2) completely!

Teacher
Teacher

Correct! The final result is (3y - 2)(2x - 1). Excellent work, everyone! Remember, practicing the regrouping technique will make you much more adept at factorising tricky expressions.

Review and Questions

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

To wrap up, factorisation by regrouping is a powerful tool. Are there any questions about the method?

Student 4
Student 4

Can this method be used on any polynomial?

Teacher
Teacher

Great question! While it can be very effective, it's not always guaranteed. Sometimes, the arrangement might not lead to a simple factorization. This is where practice matters!

Student 3
Student 3

So we just have to look carefully at the terms?

Teacher
Teacher

Exactly! Keep an eye out for those groupable terms. Always remember — 'look, regroup, factor!' Let's practice some more examples together.

Introduction to Factorisation by Regrouping

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Today, we are going to explore an interesting way to factor expressions called 'factorisation by regrouping'. Can anyone explain what they think that means?

Student 1
Student 1

Is it like finding common factors in an expression?

Teacher
Teacher

Yes, exactly! It's about reorganizing terms to find those common factors. For example, in the expression 2xy + 2y + 3x + 3, if we group the first two and the last two terms, we can see something interesting.

Student 2
Student 2

What do you see when you group them?

Teacher
Teacher

The first two terms can be factored as 2y(x + 1) and the last two as 3(x + 1). So we can rewrite the whole expression as (x + 1)(2y + 3).

Student 3
Student 3

I see! That helps a lot! So we rearranged to find common factors.

Teacher
Teacher

Exactly! Let's remember: 'Group to find.' If you can identify groups that can simplify an expression, you'll unveil common factors!

Practical Example of Regrouping

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Consider the expression 6xy - 4y + 6 - 9x. Can anyone identify potential groups here?

Student 2
Student 2

Maybe we can group 6xy with -9x and -4y with 6?

Teacher
Teacher

Great observation! Let's try that. If we rearrange it as 6xy - 9x - 4y + 6, we can factor the first group as 3(3y - 2) and the second group as -1(3y - 2).

Student 1
Student 1

So we can factor out (3y - 2) completely!

Teacher
Teacher

Correct! The final result is (3y - 2)(2x - 1). Excellent work, everyone! Remember, practicing the regrouping technique will make you much more adept at factorising tricky expressions.

Review and Questions

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

To wrap up, factorisation by regrouping is a powerful tool. Are there any questions about the method?

Student 4
Student 4

Can this method be used on any polynomial?

Teacher
Teacher

Great question! While it can be very effective, it's not always guaranteed. Sometimes, the arrangement might not lead to a simple factorization. This is where practice matters!

Student 3
Student 3

So we just have to look carefully at the terms?

Teacher
Teacher

Exactly! Keep an eye out for those groupable terms. Always remember — 'look, regroup, factor!' Let's practice some more examples together.

Introduction & Overview

Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.

Quick Overview

This section teaches the method of factorisation by regrouping terms in algebraic expressions, highlighting the process through specific examples.

Standard

Factorisation by regrouping involves rearranging terms in an expression to reveal common factors, enabling the expression to be rewritten as a product of simpler expressions. The section illustrates this method with examples such as 2xy + 2y + 3x + 3, emphasizing the importance of recognizing groupable terms.

Detailed

Detailed Summary

In this section, we explore the method of factorisation by regrouping terms, which is particularly useful in algebraic expressions where no single common factor is apparent. The process begins by identifying terms that can be grouped based on shared factors. For example, in the expression 2xy + 2y + 3x + 3, we can observe that the first two terms share 2y as a common factor, while the last two terms share 3. This allows us to factor each group individually:

  • 2xy + 2y = 2y(x + 1)
  • 3x + 3 = 3(x + 1)

This results in the expression being rewritten as (x + 1)(2y + 3). The significance of this method lies in its utility for expressions where obvious single factors do not exist, enabling a clearer pathway to factorisation. Furthermore, the technique encourages a deeper understanding of the relationship between terms and the common factors they may contain. Through multiple examples and explanations, students can develop skills to recognise how to rearrange terms effectively for factorisation.

Example : Factorise 5xy - 10y + 15 - 5x.

Solution:
Step 1
Check if there is a common factor among all terms. There is none.
Step 2
Think of grouping. Notice that the first two terms have a common factor of 5y:

5xy - 10y = 5y(x - 2)

What about the last two terms? Observe them. If you change their order to -5x + 15, it will come out:

-5x + 15 = -5(x - 3)

Step 3
Putting (a) and (b) together,

5xy - 10y + 15 - 5x = 5y(x - 2) - 5(x - 3) = 5y(x - 2) - 5(x - 3)

The factors of (5xy - 10y + 15 - 5x) are (5y - 5)(x - 2)

Youtube Videos

Class 8 Maths Chapter 14 | Factorisation by Regrouping Terms - Factorisation
Class 8 Maths Chapter 14 | Factorisation by Regrouping Terms - Factorisation
Factorisation Through Regrouping Terms - Factorisation | Class 8 Mathematics Chapter 12 | CBSE
Factorisation Through Regrouping Terms - Factorisation | Class 8 Mathematics Chapter 12 | CBSE
Class 8 | chap 14 | Factorisation | by regrouping terms
Class 8 | chap 14 | Factorisation | by regrouping terms
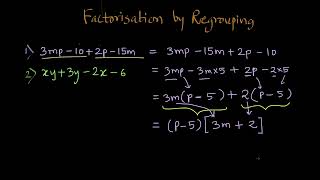
Factorisation by regrouping of non quadratics| Factorisation | NCERT Class 8 | Math | Khan Academy
Factorisation by regrouping of non quadratics| Factorisation | NCERT Class 8 | Math | Khan Academy
FACTORISATION//CH-14//CLASS 8//METHOD OF FACTORISATION--BY REGROUPING TERMS// MATHSPEDIA
FACTORISATION//CH-14//CLASS 8//METHOD OF FACTORISATION--BY REGROUPING TERMS// MATHSPEDIA
Factorisation using regrouping of terms U-14 class.8
Factorisation using regrouping of terms U-14 class.8
Factorization in One Shot | Maths - Class 8th | Umang | Physics Wallah
Factorization in One Shot | Maths - Class 8th | Umang | Physics Wallah
Factorization by regrouping terms.
Factorization by regrouping terms.
Factorization: Grouping Method | Algebraic expressions | Class 8 | CBSE | NCERT | ICSE
Factorization: Grouping Method | Algebraic expressions | Class 8 | CBSE | NCERT | ICSE

Audio Book

Dive deep into the subject with an immersive audiobook experience.

Introduction to Regrouping Terms

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Look at the expression 2xy + 2y + 3x + 3. You will notice that the first two terms have common factors 2 and y and the last two terms have a common factor 3. But there is no single factor common to all the terms. How shall we proceed?

Detailed Explanation

In the expression 2xy + 2y + 3x + 3, we first identify groups of terms that have common factors. The first two terms, 2xy and 2y, share a common factor of 2y, while the last two terms, 3x and 3, share a common factor of 3. However, there’s no common factor linking all four terms together. To factor this expression, we need to regroup these terms in a way that allows us to isolate the common factors.

Examples & Analogies

Imagine you are organizing a collection of items where some are in groups while others are individual items. To streamline your organization, you first group related items together and look for similar features within those groups, much like how we identify common factors within groups of terms.

Factoring the First Group

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Let us write (2xy + 2y) in the factor form: 2xy + 2y =(2 × x × y) + (2 × y) = (2y × x) + (2y × 1) = 2y (x + 1)

Detailed Explanation

We start by focusing on the first group of terms: 2xy and 2y. Both of these terms share a common factor of 2y. To factor them, we express each term in a way that highlights this common factor. For 2xy, we can view it as (2y × x), and for 2y, we can denote it as (2y × 1). Then, we can factor out 2y from both terms, resulting in 2y(x + 1).

Examples & Analogies

Think of this as sharing cookies. You have two types of cookies where some have chocolate chips (2xy) and others are plain (2y). Both types come from the same batch of cookie dough (2y), allowing you to express their relationship clearly before sharing them with friends later.

Factoring the Second Group

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Similarly, 3x + 3 = (3 × x) + (3 × 1) = 3 (x + 1)

Detailed Explanation

Next, we analyze the last two terms: 3x and 3. These terms share a common factor of 3. By factoring this out, we express 3x as (3 × x) and 3 as (3 × 1). Thus, we arrive at the factorization 3(x + 1). This step mirrors the previous step, establishing a similar pattern in our overall expression.

Examples & Analogies

Imagine again you have several boxes of cookies (3x and 3). The number three represents how many boxes you have, and each box is filled with the same kind of cookies. By factoring out the number 3, you’re essentially recognizing that you have uniform collections of this type.

Combining the Factored Groups

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Hence, 2xy + 2y + 3x + 3 = 2y (x + 1) + 3 (x + 1) = (x + 1) (2y + 3)

Detailed Explanation

Now, we combine the factored forms from both groups. We found that 2xy + 2y factors into 2y(x + 1) and 3x + 3 factors into 3(x + 1). By recognizing that both resulting terms include the common factor (x + 1), we can factor that out. This gives us (x + 1)(2y + 3), a simplified product of factors.

Examples & Analogies

It's like putting together two similar groupings of items. Once you’ve separated cookies into their respective categories (chocolate chip and plain), you can create a combined cookie platter (product of factors) where guests can easily select from the cookies they like. You’ve organized them well for your friends.

Understanding Regrouping

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

What is regrouping? Suppose, the above expression was given as 2xy + 3 + 2y + 3x; then it will not be easy to see the factorisation...

Detailed Explanation

Regrouping refers to rearranging terms in an expression to highlight common factors. In our example, if we initially had the expression 2xy + 3 + 2y + 3x, it could be challenging to see possible groupings for factorization. By rearranging it into the order 2xy + 2y + 3x + 3, we create clearer groups that allow us to perform factorization effectively.

Examples & Analogies

Consider putting together a puzzle. Sometimes you need to move pieces around to see how they fit together better. By rearranging the pieces (or terms), you might uncover connections that were hidden in the original layout.

Example of Regrouping

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Let us try: 2xy + 3x + 2y + 3 = 2 × x × y + 3 × x + 2 × y + 3.

Detailed Explanation

In this example, we regroup the terms as follows: (2xy + 3x) + (2y + 3). Each group can be factored separately: For the first group, we can factor out 'x' giving us x(2y + 3), and for the second group, we can factor out 1, giving us 1(2y + 3). This results in the expression (2y + 3)(x + 1), demonstrating a different approach to reaching the same factors.

Examples & Analogies

Imagine you are organizing books by genre. If you rearranged books on a shelf to group romance books together and sci-fi books in another area, you’d see clearer categories. Just like this, regrouping terms enables us to see connections in algebra that aren’t apparent until rearranged.

Definitions & Key Concepts

Learn essential terms and foundational ideas that form the basis of the topic.

Key Concepts

  • Factorisation by Regrouping: A method to factor expressions by reorganizing them into groups that reveal common factors.

  • Identifying Common Factors: Look for similarities between terms to group potential factors.

  • Rearrangement Technique: The technique involves rearranging terms to facilitate easy grouping.

Examples & Real-Life Applications

See how the concepts apply in real-world scenarios to understand their practical implications.

Examples

  • Example: Factorising 2xy + 2y + 3x + 3 results in (x + 1)(2y + 3).

  • Example: Factorising 6xy - 4y + 6 - 9x leads to (3y - 2)(2x - 1).

Memory Aids

Use mnemonics, acronyms, or visual cues to help remember key information more easily.

🎵 Rhymes Time

  • To group and to factor is quite a fun game, rearranging the terms will lead you to fame!

📖 Fascinating Stories

  • Once there was a wise math wizard who loved to solve puzzles. One day he faced a tricky expression, but he rearranged the numbers, grouping them cleverly until they revealed hidden treasures—common factors.

🧠 Other Memory Gems

  • RAP - Rearrange, Analyze, and Factor.

🎯 Super Acronyms

GFG - Group Factors Gradually.

Flash Cards

Review key concepts with flashcards.

Glossary of Terms

Review the Definitions for terms.

  • Term: Regrouping

    Definition:

    The process of rearranging terms in an expression to form manageable groups that reveal common factors.

  • Term: Common Factor

    Definition:

    A number or term that divides two or more numbers or terms evenly.

  • Term: Factorisation

    Definition:

    The process of breaking down an expression into its constituent factors.

  • Term: Irreducible Factors

    Definition:

    Factors that cannot be further broken down into simpler components.

Similar Question

Factorise 8ab - 4a + 12 - 4b.

Solution:
Step 1
Check if there is a common factor among all terms. There is none.
Step 2
Think of grouping. Notice that the first two terms have a common factor of 4:

4(2ab - a)

What about the last two terms? Observe them. If you change their order to -4b + 12, it will come out:

-4b + 12 = -4(b - 3)

Step 3
Putting (a) and (b) together,

8ab - 4a + 12 - 4b = 4(2ab - a) - 4(b - 3) = 4(2ab - a - b + 3)

The factors of (8ab - 4a + 12 - 4b) are (4)(2ab - a - b + 3)