Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Factors
Unlock Audio Lesson

Today we will learn about factors of natural numbers. Can anyone tell me what a factor is?

Isn't it a number that divides another number evenly?

Exactly! For example, if we take the number 30, we can express it as 30 = 2 × 15. That means both 2 and 15 are factors of 30.

So, what are all the factors of 30?

Great question! The complete list of factors for 30 is 1, 2, 3, 5, 6, 10, 15, and 30. Remember, 1 is a factor of every natural number!

Can we use any number to find its factors?

Yes, any positive integer can be analyzed for its factors.

What about the prime factors of 30?

The prime factorization of 30 is 2 × 3 × 5. Prime factors are important as they form the basis for other numbers!

To summarize, factors are numbers that divide another number evenly, and 30 has both its factors and prime factors. Can someone name the prime factors of any other number?
Prime Factorization
Unlock Audio Lesson

Now let's focus more on prime factors. Who can remind me what they are?

Prime factors are the factors that are prime numbers.

Exactly! For instance, the number 70 can be expressed as 2 × 5 × 7, and those are its prime factors. Why is knowing the prime factorization useful?

It helps in simplifying complex fractions and solving problems!

Correct! Let's look at the prime factors for the number 90. How would we break that down?

90 = 2 × 3 × 3 × 5!

Excellent! Prime factorization is critical in number theory and mathematics as a whole. Who can tell me how to factorize a number?

We start by dividing by prime numbers until we're left with 1!

Well done! Let's remember this when we study algebraic expressions in the next sections.
Practical Applications
Unlock Audio Lesson

Factors are not just about numbers; they are used in many real-life scenarios. Can anyone think of an application?

Like organizing things into groups of equal size?

Exactly! If you have 30 apples and want to divide them into groups of 5, how many groups can you make?

Six groups!

Correct! This is how important factors are in day-to-day situations. Understanding factors allows us to manage quantities effectively. Can you see how this skill is applied in business or even cooking?

Yes, you need to know how to divide ingredients or allocate items!

Precisely! Remember, factors help in making decisions in a practical manner. Let's recap what we've learned today.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section discusses how to identify factors of natural numbers, emphasizing the concept of prime factors and factor forms. It highlights that every natural number can be expressed as a product of its factors and introduces the notion of prime factorization as a way to break down composite numbers into their building blocks.
Detailed
Factors of Natural Numbers
In this section, we explore the concept of factors related to natural numbers. A factor is defined as a number that divides another number evenly without leaving a remainder. For example, the number 30 can be expressed as a product of its factors in different ways, such as:
- 30 = 2 × 15
- 30 = 3 × 10
- 30 = 5 × 6
- 30 = 1 × 30
From these equations, we can deduce that the factors of 30 include 1, 2, 3, 5, 6, 10, 15, and 30. Additionally, every natural number has 1 as a factor, making it a universal factor.
Prime Factors and Factorization
Among these factors, certain numbers are classified as prime factors, which are the building blocks of composite numbers. For instance, the prime factorization of 30 is 2 × 3 × 5, indicating that it consists of three prime factors. Prime factorization is crucial for simplifying arithmetic operations and understanding number properties.
Summary
Understanding factors and their prime counterparts helps students solve problems involving divisibility, fractions, and algebraic expressions. Each natural number can be expressed as a product of its factors, providing essential insight into number theory.
Youtube Videos




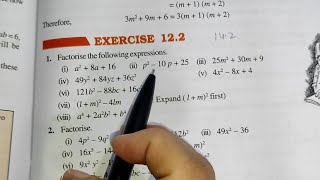





Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Factors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
You will remember what you learnt about factors in Class VI. Let us take a natural number, say 30, and write it as a product of other natural numbers, say 30 = 2 × 15. We know that 30 can also be written as 3 × 10 = 5 × 6 = 1 × 30. Thus, 1 and 30 are also factors of 30. Thus, 1, 2, 3, 5, 6, 10, 15 and 30 are the factors of 30.
Detailed Explanation
In this chunk, we start by recalling the concept of factors. A factor of a number is any whole number that can be multiplied by another whole number to produce that number. For instance, the number 30 can be expressed as the product of 2 and 15, among other combinations. These products show all the possible pairs of numbers that multiply to give 30. Additionally, 1 and 30 itself are factors of 30, making the complete list of factors for 30 to be 1, 2, 3, 5, 6, 10, 15, and 30. Understanding factors helps in various areas of mathematics, including simplification and factorization of algebraic expressions.
Examples & Analogies
Think of factors as teams of friends working together to achieve a common goal, which in this case is reaching the number 30. Each team represents a pair of factors—like the 2-person team (2 and 15) working together to reach the target of 30. Similarly, a group of three friends could team up (3, 10) or four friends (5, 6) creating other combinations. The number 30 allows many different groups to achieve its value, just as in real life, teams can be formed in multiple ways to accomplish tasks.
Prime Factors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Of these, 2, 3 and 5 are the prime factors of 30 (Why?). A number written as a product of prime factors is said to be in the prime factor form; for example, 30 written as 2 × 3 × 5 is in the prime factor form. The prime factor form of 70 is 2 × 5 × 7. The prime factor form of 90 is 2 × 3 × 3 × 5, and so on.
Detailed Explanation
In this chunk, we differentiate between regular factors and prime factors. Prime factors are those that can only be divided by 1 and themselves without leaving a remainder. In our case for number 30, we identify 2, 3, and 5 as prime factors because they meet this criterion. When we express a number as a product of its prime factors, like 30 as 2 x 3 x 5, we take it to its simplest form, known as the prime factor form. Similarly, the prime factor forms for 70 and 90 illustrate this concept further.
Examples & Analogies
Imagine prime factors are like the fundamental building blocks or LEGO pieces that cannot be broken down into smaller pieces. Just as you can build complex structures using basic LEGO bricks, you can create larger numbers using these basic prime factors—the building blocks of mathematics. For example, the number 30 is built by combining these prime LEGO blocks: 2, 3, and 5.
Importance of the Number 1
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
You will notice that 1 is a factor of any number. For example, 1 × 101 = 101. However, when we write a number as a product of factors, we shall not write 1 as a factor, unless it is specially required.
Detailed Explanation
This chunk highlights the unique role of the number 1 in factorization. The number 1 is a universal factor for all natural numbers since any number multiplied by 1 remains unchanged. While it's technically a factor, often for simplicity, we don't include it when listing factors, unless specifically needed. This understanding simplifies our work when factoring larger numbers or algebraic expressions.
Examples & Analogies
Consider the number 1 as a special key that can unlock any door (i.e., any natural number). It’s universally applicable so no matter what number you have, you can always use the key (1) to derive it. Yet, when telling others about the locks you can open (i.e., factors), you don’t typically mention the key. You focus on the unique keys that open different doors.
Summary of Factors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A number written as a product of prime factors is said to be in the prime factor form; for example, 30 written as 2 × 3 × 5 is in the prime factor form. Similarly, we can express algebraic expressions as products of their factors.
Detailed Explanation
This chunk concludes the section by reaffirming the importance of expressing numbers in their prime factor form and extends the concept to algebraic expressions. Just like numerical factors, algebraic expressions can also be factored into simpler constituent parts. This will be critical when we advance to factorization in algebra, allowing us to break down complex expressions into manageable components.
Examples & Analogies
Think of prime factorization like organizing ingredients for a recipe. Just as you may break down complex recipes into single ingredients (the simplest forms of food), we can break down numbers and algebraic expressions into their 'ingredient' factors. This organization is essential for cooking (solving) and ensures we have a clear path to understanding the final dish (solving an equation or simplifying).
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Factors: Numbers that divide another number without leaving a remainder.
-
Prime Factors: Prime numbers that are factors of a given number.
-
Prime Factorization: The expression of a number as the product of its prime factors.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The factors of 30 are 1, 2, 3, 5, 6, 10, 15, and 30.
-
The prime factorization of 90 is 2 × 3 × 3 × 5.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Factors gather round in pairs, divide with ease, without any cares.
📖 Fascinating Stories
-
Imagine a farmer with 30 apples. He wants to share with 2, 3, 5 friends. Every friend gets apples, and no one is left without!
🧠 Other Memory Gems
-
F.A.C.T (Factors Always Come Together) - to remember that factors will always pair with divisors.
🎯 Super Acronyms
P.A.R.T (Prime Assembles Real Numbers Together) - to remember that prime factors combine to form composite numbers.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Factors
Definition:
Numbers that divide a given number evenly without leaving a remainder.
-
Term: Prime Factors
Definition:
Factors that are prime numbers, meaning they have only two distinct positive divisors: 1 and themselves.
-
Term: Prime Factorization
Definition:
Expressing a number as the product of its prime factors.
