Learn
Games

12.2.1 - Method of common factors

Interactive Audio Lesson

Listen to a student-teacher conversation explaining the topic in a relatable way.

Introduction to Common Factors

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Today, we're going to explore how to factorize expressions using common factors. Can anyone tell me what a factor is?

Student 1
Student 1

A factor is a number or expression that can be multiplied to get another number or expression.

Teacher
Teacher

Great! So, when we talk about common factors, we mean factors that are shared by different terms in an expression. For instance, in the expression 2x + 4, can someone show me how we can break that down?

Student 2
Student 2

We can write 2x as 2 times x, and 4 as 2 times 2.

Teacher
Teacher

Exactly! So we notice that 2 is a common factor. By factorizing, we can write it as 2(x + 2). This makes simplifying expressions easier. Who can summarize why we do this?

Student 3
Student 3

We factor expressions to find their simplest form and understand their components better.

Teacher
Teacher

Well done! Now let’s look at another example to solidify our understanding.

Working with More Complex Expressions

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Let’s factor 5xy + 10x. What do we notice here?

Student 4
Student 4

Both terms seem to have 5 and x as common factors!

Teacher
Teacher

Excellent! So how can we express that?

Student 1
Student 1

We can write it as 5x(y + 2).

Teacher
Teacher

Correct! Remember, identifying common factors not only helps to simplify but also to solve equations quicker. Can we think of another similar expression to practice?

Student 2
Student 2

How about 12a^2b + 15ab^2?

Teacher
Teacher

Great choice! Let’s factor this expression together.

Exploring Factorization through Grouping

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

In some cases, like 2xy + 2y + 3x + 3, we might have to group terms strategically. Why do you think that is?

Student 3
Student 3

Because not all terms have a direct common factor, but we can pair them to find one.

Teacher
Teacher

Exactly! Let's take the first two terms and the last two. What can we factor out from each group?

Student 4
Student 4

From the first group, we can factor out 2y, and from the second, we can factor out 3.

Teacher
Teacher

Then we can express it as 2y(x + 1) + 3(x + 1). Now that we have a common factor across the two groups, what can we do next?

Student 1
Student 1

We can factor out (x + 1) to get our final expression as (x + 1)(2y + 3).

Teacher
Teacher

Excellent work everyone! Let's summarize this process of grouping and factorization.

Introduction to Common Factors

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Today, we're going to explore how to factorize expressions using common factors. Can anyone tell me what a factor is?

Student 1
Student 1

A factor is a number or expression that can be multiplied to get another number or expression.

Teacher
Teacher

Great! So, when we talk about common factors, we mean factors that are shared by different terms in an expression. For instance, in the expression 2x + 4, can someone show me how we can break that down?

Student 2
Student 2

We can write 2x as 2 times x, and 4 as 2 times 2.

Teacher
Teacher

Exactly! So we notice that 2 is a common factor. By factorizing, we can write it as 2(x + 2). This makes simplifying expressions easier. Who can summarize why we do this?

Student 3
Student 3

We factor expressions to find their simplest form and understand their components better.

Teacher
Teacher

Well done! Now let’s look at another example to solidify our understanding.

Working with More Complex Expressions

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Let’s factor 5xy + 10x. What do we notice here?

Student 4
Student 4

Both terms seem to have 5 and x as common factors!

Teacher
Teacher

Excellent! So how can we express that?

Student 1
Student 1

We can write it as 5x(y + 2).

Teacher
Teacher

Correct! Remember, identifying common factors not only helps to simplify but also to solve equations quicker. Can we think of another similar expression to practice?

Student 2
Student 2

How about 12a^2b + 15ab^2?

Teacher
Teacher

Great choice! Let’s factor this expression together.

Exploring Factorization through Grouping

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

In some cases, like 2xy + 2y + 3x + 3, we might have to group terms strategically. Why do you think that is?

Student 3
Student 3

Because not all terms have a direct common factor, but we can pair them to find one.

Teacher
Teacher

Exactly! Let's take the first two terms and the last two. What can we factor out from each group?

Student 4
Student 4

From the first group, we can factor out 2y, and from the second, we can factor out 3.

Teacher
Teacher

Then we can express it as 2y(x + 1) + 3(x + 1). Now that we have a common factor across the two groups, what can we do next?

Student 1
Student 1

We can factor out (x + 1) to get our final expression as (x + 1)(2y + 3).

Teacher
Teacher

Excellent work everyone! Let's summarize this process of grouping and factorization.

Introduction & Overview

Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.

Quick Overview

This section introduces the method of factorization using common factors by breaking down algebraic expressions into irreducible components.

Standard

The method of common factors involves rewriting algebraic expressions as products of their irreducible factors by identifying shared factors in different terms. The process is outlined through examples, illustrating how to group terms, factor them out, and arrive at a simplified form.

Detailed

Method of Common Factors

In this section, we explore the method of common factors, a key technique in algebraic factorization. The process begins by expressing algebraic expressions as sums of terms that can be grouped based on their common factors. This method follows a systematic approach:
1. Identify Common Factors: Each term of the expression is represented as a product of its irreducible factors.
2. Group Terms: Terms with shared factors are grouped together.
3. Factor Out the Common Elements: Using distributive properties, we can extract the common factors, leading to a simplified expression.

Example: To factorize the expression 2x + 4, we first identify both terms can be expressed with the factor 2:

  • 2x = 2 × x
  • 4 = 2 × 2

Thus, rewriting yields:
2x + 4 = 2(x + 2).

The common factor method enhances understanding of algebra by simplifying expressions and lays the foundation for exploring more complex factorization techniques later in the chapter.

Youtube Videos

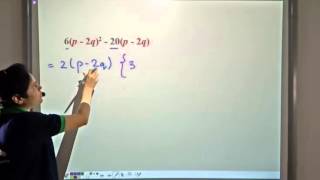
Factorization: Common Factor Method | Algebraic expressions | Class 8 | CBSE | NCERT | ICSE
Factorization: Common Factor Method | Algebraic expressions | Class 8 | CBSE | NCERT | ICSE
Class 8 Maths Chapter 14 | Method of Common Factors - Factorisation
Class 8 Maths Chapter 14 | Method of Common Factors - Factorisation
Ex-12.1 Chapter -12 Factorisation || Class 8th Maths
Ex-12.1 Chapter -12 Factorisation || Class 8th Maths
Factorisation Using Identities - Factorisation | Class 8 Maths
Factorisation Using Identities - Factorisation | Class 8 Maths
Factorisation Through Common Factors - Factorisation | Class 8 Mathematics Chapter 12 | CBSE 2024-25
Factorisation Through Common Factors - Factorisation | Class 8 Mathematics Chapter 12 | CBSE 2024-25
Factorization in One Shot | Maths - Class 8th | Umang | Physics Wallah
Factorization in One Shot | Maths - Class 8th | Umang | Physics Wallah
Class 8 Maths Chapter 14 | Factorisation by Regrouping Terms - Factorisation
Class 8 Maths Chapter 14 | Factorisation by Regrouping Terms - Factorisation
Factorization of Algebraic Expressions | Factorization Class 8 | Factorization Method | Factorize
Factorization of Algebraic Expressions | Factorization Class 8 | Factorization Method | Factorize
class 8# Factorization#ex 6.1 # Goyal brothers prakashan#youtube #mathmath #youtubeshorts
class 8# Factorization#ex 6.1 # Goyal brothers prakashan#youtube #mathmath #youtubeshorts
Factorisation by Common Factors | Hindi | Maths
Factorisation by Common Factors | Hindi | Maths

Definitions & Key Concepts

Learn essential terms and foundational ideas that form the basis of the topic.

Key Concepts

  • Identifying Common Factors: Recognizing factors shared among terms is crucial for simplifying expressions.

  • Method of Grouping: This technique involves rearranging and grouping terms strategically for effective factorization.

Examples & Real-Life Applications

See how the concepts apply in real-world scenarios to understand their practical implications.

Examples

  • Example: Factor 2x + 4 - By observing 2 is common, we rewrite as 2(x + 2).

  • Example: Factor 5xy + 10x - Recognizing both have factors 5 and x leading to 5x(y + 2).

Memory Aids

Use mnemonics, acronyms, or visual cues to help remember key information more easily.

🎵 Rhymes Time

  • To factorize we must detect, the common factor to select.

📖 Fascinating Stories

  • Once upon a time, in a land of numbers, 12 and 36 were searching for their common friend, the biggest number they could share.

🧠 Other Memory Gems

  • FIND: First Identify Number that Divides.

🎯 Super Acronyms

C-Factor

  • Common-Factor to Factorize.

Flash Cards

Review key concepts with flashcards.

Glossary of Terms

Review the Definitions for terms.

  • Term: Common Factor

    Definition:

    A factor that is shared among different terms in an expression.

  • Term: Irreducible Factor

    Definition:

    A factor that cannot be further broken down into simpler components.

  • Term: Factorization

    Definition:

    The process of breaking down an expression into a product of its factors.

  • Term: Distributive Law

    Definition:

    A mathematical property allowing the multiplication of a single term across terms in parentheses.