Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Prime Factorization
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're going to learn about square roots, specifically how to find them using prime factorization. Can anyone explain what a prime number is?
A prime number is a whole number greater than 1 that has no positive divisors other than 1 and itself.
Correct! Now, can someone give me an example of a prime number?
2, 3, 5, and 7 are prime numbers.
Great! So to find a square root using prime factorization, we first need to factor our number into primes. Letβs try 36. Who can tell me the prime factors of 36?
36 can be factored into 2 Γ 2 Γ 3 Γ 3.
Exactly, and how do we find the square root from here?
We group the primes in pairs. So we have (2 Γ 3)Β², which gives us 6.
Well done! So the square root of 36 is 6. Remember this pairing; itβs crucial for our next problems.
Using Prime Factorization to Find Square Roots
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now letβs find the square root of a number like 144. What is its prime factorization?
144 = 2 Γ 2 Γ 2 Γ 2 Γ 3 Γ 3 or 144 = 2^4 Γ 3^2.
Good job! Now how would we find the square root?
We pair the factors as (2 Γ 3)Β² giving us 12.
Exactly! Let's attempt one more. How about 324? What do we do first?
First, we factor it into primes: 324 = 2 Γ 2 Γ 3 Γ 3 Γ 3 Γ 3.
Great! Now pair them together.
We get (2 Γ 3 Γ 3)Β², which means the square root is 18.
Correct! Remember, practice makes perfect, so keep practicing with various numbers.
Applications of Square Roots in Real Life
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs talk about where we might use square roots in real life. Can anyone provide an example?
If we want to calculate the side length of a square garden if we know the area.
Exactly! If the area is 144 mΒ², we find the side length by taking the square root, which gives us 12 m.
What about in construction?
Great point! In construction, square roots can help determine diagonal measurements using the Pythagorean theorem. So if one side is 6 m and another is 8 m, you can find the diagonal using the square root of (6Β² + 8Β²) = 10 m.
I see why understanding square roots is important!
Exactly! They are crucial for precise calculations in various fields. Letβs keep that in mind for more advanced topics.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explains the process of finding square roots through prime factorization, emphasizing how each prime factor in the square's prime factorization occurs twice as often as in the number itself. Additionally, it describes how to identify perfect squares and how to complete pairs for non-perfect squares.
Detailed
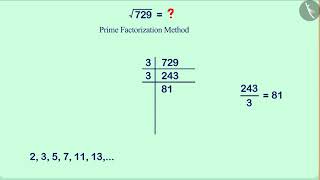
Finding Square Roots through Prime Factorization
To find the square root of a number using prime factorization, we first express the number as a product of its prime factors. For a perfect square, each prime factor will occur an even number of times. For example, considering the number 36:
- Prime factorization of 36 is:
36 = 2 Γ 2 Γ 3 Γ 3. Each prime factor (2 and 3) occurs twice.
When we find the square root of 36, we group the prime factors in pairs:
t = (2 Γ 3)Β².
Thus, the square root of 36 is 6.
In contrast, if we analyze a number like 90,
t = 90 = 2 Γ 3 Γ 3 Γ 5,
it is not a perfect square since 2 and 5 do not have pairs. We learn that to form a perfect square, we can multiply the number by the missing factors necessary to complete the pairs.
The significance of this method lies in its effectiveness for larger numbers or identifying perfect squares, which is useful in various mathematical applications.
Similar Questions
- Example: Is 1440 a perfect square? If not, find the smallest multiple of 1440 that is a perfect square. Find the square root of the new number.
Solution: We have 1440 = 2^5 \times 3^2 \times 5^1.
The prime factor 5 has no pair, thus 1440 is not a perfect square. So, we multiply 1440 by 5 to get,
1440 \times 5 = 7200 = 2^5 \times 3^2 \times 5^2.
Now each prime factor has a pair. Therefore, 7200 is a perfect square.
Thus, the required smallest multiple of 1440 which is a perfect square is 7200, with a square root of 84.
\( \sqrt{7200} = 60 \)
- Example 8: Is 5000 a perfect square? If not, find the smallest multiple of 5000 which is a perfect square. Find the square root of this new number.
Solution: We have 5000 = 2^3 \times 5^4.
The prime factor 2 has no pair, thus 5000 is not a perfect square. If we multiply by 2, we get 10000 = 2^4 \times 5^4, which is a perfect square.
Thus, the required number is \( 10000 \), with a square root of \( \sqrt{10000} = 100 \).
- Example 9: Is 2500 a perfect square? If not, find the smallest multiple of 2500 that is a perfect square. Then, find the square root of this new number.
Solution: We have 2500 = 2^2 \times 5^4.
Since all prime factors have pairs, 2500 is a perfect square itself. The square root is \( \sqrt{2500} = 50 \).
- Example 10: Is 980 a perfect square? If not, determine the smallest multiple of 980 that becomes a perfect square, and find the square root of this new number.
Solution: We have 980 = 2^2 \times 5^1 \times 7^2.
The prime factor 5 has no pair, thus 980 is not a perfect square. By multiplying by 5, we get 4900 = 2^2 \times 5^2 \times 7^2 which is perfect.
Hence, the smallest multiple of 980 which is a perfect square is 4900, giving a square root of \( \sqrt{4900} = 70 \).
- Example 11: Is 850 a perfect square? If not, locate the smallest multiple of 850 which is a perfect square, and compute the square root of this new number.
Solution: We have 850 = 2^1 \times 5^2 \times 17^1.
The prime factors 2 and 17 have no pairs, thus 850 is not a perfect square. Multiplying by 34 results in 28900 = 2^2 \times 5^2 \times 17^2, which is a perfect square. Therefore, the smallest multiple is 28900, with a square root of \( \sqrt{28900} = 170 \).
Youtube Videos
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Prime Factorization: The process of breaking down numbers into prime factors.
-
Perfect Squares: Whole numbers that can be expressed as the square of another integer.
-
Finding Square Roots: The method of identifying the square root through pairing prime factors.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of perfect square: 36 which equals 6 Γ 6.
-
Example of non-perfect square: 90 which can not be perfectly paired in factorization.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
A square, a perfect pair, when factors meet they'll make a square.
π Fascinating Stories
-
Once there was a number named 36 who always sought partnerships. When it found 2Γ2 and 3Γ3, it danced joyfully to become 6 and 6.
π§ Other Memory Gems
-
To find roots we use factors: pair up to share, the evenness will make it fair.
π― Super Acronyms
PAIR
- Prime factors Are In Representation for roots.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Prime Factorization
Definition:
Breaking down a number into the product of its prime factors.
-
Term: Perfect Square
Definition:
A number that can be expressed as the square of an integer.
-
Term: Square Root
Definition:
A value that, when multiplied by itself, gives the original number.
-
Term: Pairing
Definition:
Grouping prime factors in twos to determine square roots.