5 - Squares and Square Roots

Interactive Audio Lesson

Listen to a student-teacher conversation explaining the topic in a relatable way.

Introduction to Square Numbers

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Today we’ll talk about square numbers. Does anyone know what a square number is?

Student 1
Student 1

Isn't it the number you get when you multiply a number by itself?

Teacher
Teacher

Exactly! For example, 3 multiplied by itself gives us 9, which is 3 squared. We represent this as 3². Can anyone list other square numbers?

Student 2
Student 2

1, 4, 9, 16, and 25!

Teacher
Teacher

Great job! These numbers all can be expressed as n². Remember, square numbers are foundational in mathematics.

Properties of Square Numbers

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Let’s dive deeper into the properties. For instance, what can you tell me about the unit digits of square numbers?

Student 3
Student 3

They end with 0, 1, 4, 5, 6, or 9!

Teacher
Teacher

Exactly! And if a number ends with 2, 3, 7, or 8, it cannot be a square number. Can anyone explain why?

Student 4
Student 4

Because those digits can't be formed by squaring whole numbers.

Teacher
Teacher

Correct. Let's also note that only square numbers can have even numbers of zeros at their end. Good observations!

Finding Square Roots

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Now, let’s talk about square roots. Does anyone know how to find the square root of a number?

Student 1
Student 1

We can do that by trying to find what number, when squared, will give us our original number!

Teacher
Teacher

Exactly! There are several methods to find square roots, including repeated subtraction and prime factorization. For example, to find √36, we can see that 6 × 6 = 36.

Student 2
Student 2

Is there a faster method for bigger numbers?

Teacher
Teacher

Good question! We will explore the long division method for finding square roots of larger numbers.

Introduction & Overview

Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.

Quick Overview

This section introduces the concepts of square numbers and their properties, alongside methods for calculating square roots.

Standard

In this section, we explore square numbers, their properties, and methods for determining square roots. Key concepts include square numbers, patterns, and square root operations. Real-world applications, exercises, and alternative strategies are also presented to solidify understanding.

Detailed

Squares and Square Roots

Overview

The section delves into understanding square numbers, defined as the product of natural numbers with themselves, such as 1, 4, 9, and so on. Additionally, we examine various properties of square numbers, including their patterns, how to determine whether a number is a perfect square, and methods for calculating square roots.

Key Concepts

  • Square Numbers: Natural numbers that can be expressed as the product of a number with itself, denoted as n².
  • Properties of Square Numbers: Observations that provide insights into the characteristics of square numbers, particularly ending digits.
  • Methods for Finding Square Roots: Including techniques like repeated subtraction and prime factorization, helping students find square roots both numerically and conceptually.

The section promotes critical thinking with exercises and interactive dialogues that foster comprehension, ensuring students grasp the relationship between squares and their roots.

Youtube Videos

Do you remember the square roots of these perfect squares? 🤯 #Shorts #math #maths #mathematics
Do you remember the square roots of these perfect squares? 🤯 #Shorts #math #maths #mathematics
Square and Square Roots in One Shot | Maths - Class 8th | Umang | Physics Wallah
Square and Square Roots in One Shot | Maths - Class 8th | Umang | Physics Wallah
Cube Root Math Trick
Cube Root Math Trick
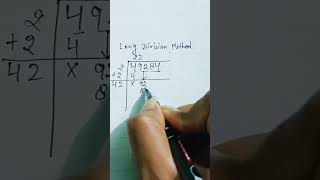
long division method for square root class 8th #mathstricks #lovemaths
long division method for square root class 8th #mathstricks #lovemaths
Convert imperfect square root into numbers @Mathshackshub #trending #maths #square #shorts
Convert imperfect square root into numbers @Mathshackshub #trending #maths #square #shorts
Squares and Square Roots - Full Chapter Explanation & Exercise | Class 8 Maths Chapter 6
Squares and Square Roots - Full Chapter Explanation & Exercise | Class 8 Maths Chapter 6
Squares and Square Roots - Exercise 5.1 | Class 8 Maths Chapter 5 | CBSE 2024-25
Squares and Square Roots - Exercise 5.1 | Class 8 Maths Chapter 5 | CBSE 2024-25
#Maths Working Model #cube root working model #Maths TLM #viral project #square root #viral#project👍
#Maths Working Model #cube root working model #Maths TLM #viral project #square root #viral#project👍
Squares and Square Roots || 8 Min || CBSE Class 8 Math Rapid Revision || Ayush Sir
Squares and Square Roots || 8 Min || CBSE Class 8 Math Rapid Revision || Ayush Sir
Class 8th | Maths | Squares and Square Roots in One Shot | Last Minute Revision Series 🔥
Class 8th | Maths | Squares and Square Roots in One Shot | Last Minute Revision Series 🔥

Audio Book

Dive deep into the subject with an immersive audiobook experience.

Introduction to Square Numbers

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

You know that the area of a square = side × side (where ‘side’ means ‘the length of a side’). Study the following table.

Side of a square (in cm) Area of the square (in cm²)
1 1 × 1 = 1 = 1²
2 2 × 2 = 4 = 2²
3 3 × 3 = 9 = 3²
5 5 × 5 = 25 = 5²
8 8 × 8 = 64 = 8²
a a × a = a²

What is special about the numbers 4, 9, 25, 64 and other such numbers? Since, 4 can be expressed as 2 × 2 = 2², 9 can be expressed as 3 × 3 = 3², all such numbers can be expressed as the product of the number with itself. Such numbers like 1, 4, 9, 16, 25, ... are known as square numbers. In general, if a natural number m can be expressed as n², where n is also a natural number, then m is a square number.

Detailed Explanation

A square number is the product of a number multiplied by itself. For example, the area of a square with each side measuring 2 cm is 2 × 2 = 4 cm². This means the number 4 is a square number. Similarly, 1, 4, 9, 16, etc. can be represented as 1², 2², 3², and 4² respectively because they result from squaring whole numbers.

Examples & Analogies

Imagine you have a square piece of paper. If each side of the paper is 3 cm long, when you calculate the area (how much paper you have), you're really calculating 3 × 3 or 3², which equals 9 cm². Thus, 9 is a square number.

Identifying Square Numbers

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Consider the following numbers and their squares.

Number Square
1 1 × 1 = 1
2 2 × 2 = 4
3 3 × 3 = 9
4 4 × 4 = 16
Can you complete it?

From the above table, can we enlist the square numbers between 1 and 100?

Detailed Explanation

To find the square numbers between 1 and 100, we list the squares of whole numbers. The square of 1 is 1, the square of 2 is 4, the square of 3 is 9, and this continues up to the square of 10 which is 100. Therefore, the square numbers from 1 to 100 are: 1, 4, 9, 16, 25, 36, 49, 64, 81, and 100.

Examples & Analogies

Think of a garden with flower beds shaped like squares. If the side of a bed is 4 meters, you can calculate how much space it takes up (its area) by doing 4 × 4, which tells you the entire area is 16 square meters. Each of these unique areas corresponds to square numbers.

Properties of Square Numbers

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Study the square numbers in the above table. What are the ending digits (that is, digits in the units place) of the square numbers? All these numbers end with 0, 1, 4, 5, 6 or 9 at units place. None of these end with 2, 3, 7 or 8 at unit’s place. Can we say that if a number ends in 0, 1, 4, 5, 6 or 9, then it must be a square number?

Detailed Explanation

Observing the table of square numbers, we see that squares of whole numbers exhibit certain patterns in their last digit. Specifically, a square number can only end in 0, 1, 4, 5, 6, or 9. That means if you have a number ending in those digits, it has the potential to be a square number, but it’s not guaranteed.

Examples & Analogies

If you have a set of cards and you flip them over to see their numbers, you might notice that only a few cards show a specific number like 5 or 6 at the end. Similarly, square numbers behave in this way where certain last digits are more common while others are excluded.

Finding Square Roots

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Study the following situations... In all the above cases, we need to find a number whose square is known. Finding the number with the known square is known as finding the square root.

Detailed Explanation

The process of finding the square root is essentially the reverse of squaring a number. For example, if we know the area of a square is 36 cm², we need to find what number squared gives us that area. Thus, the square root of 36 is 6, as 6 × 6 = 36.

Examples & Analogies

Imagine you have a square garden with an area of 144 m². To know how long each side is, you would calculate the square root. By determining the square root, you're solving the puzzle of figuring out how wide each side must be to reach that total area.

Finding Square Roots by Prime Factorization

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Consider the prime factorization of the following numbers and their squares...

Prime factorization of a Number Prime factorization of its Square
6 = 2 × 3 36 = 2 × 2 × 3 × 3
8 = 2 × 2 × 2 64 = 2 × 2 × 2 × 2 × 2 × 2
...

Detailed Explanation

When we find the square root using prime factorization, we look for pairs of factors. For example, if you have the factorization of 36 as 2 × 2 × 3 × 3, you can group them into pairs: (2 × 2) and (3 × 3). Taking one factor from each pair gives 2 × 3, which equals 6, the square root of 36.

Examples & Analogies

Think of a book shelf where you store books in pairs. If you have 36 books arranged, by pairing them, you can see there are 18 pairs. Taking one book from each pair illustrates how the square root allows us to find half of the total when organized suitably.

Definitions & Key Concepts

Learn essential terms and foundational ideas that form the basis of the topic.

Key Concepts

  • Square Numbers: Natural numbers that can be expressed as the product of a number with itself, denoted as n².

  • Properties of Square Numbers: Observations that provide insights into the characteristics of square numbers, particularly ending digits.

  • Methods for Finding Square Roots: Including techniques like repeated subtraction and prime factorization, helping students find square roots both numerically and conceptually.

  • The section promotes critical thinking with exercises and interactive dialogues that foster comprehension, ensuring students grasp the relationship between squares and their roots.

Examples & Real-Life Applications

See how the concepts apply in real-world scenarios to understand their practical implications.

Examples

  • The square of 5 is 25, as 5 × 5 = 25.

  • The square root of 36 is 6, since 6 × 6 = 36.

Memory Aids

Use mnemonics, acronyms, or visual cues to help remember key information more easily.

🎵 Rhymes Time

  • Squares are fair, times two in a pair, one, four, and nine, they shine so fine!

📖 Fascinating Stories

  • Once upon a time, numbers wanted to know their friends. They squared each other to see who ends up perfect. They found themselves in pairs forming beautiful squares.

🧠 Other Memory Gems

  • To remember square numbers: S = Side, P = Perimeter, A = Area, C = Count down: 1, 4, 9...

🎯 Super Acronyms

SQUARE = Some Quick Ways Are Really Excellent (methods for calculating squares).

Flash Cards

Review key concepts with flashcards.

Glossary of Terms

Review the Definitions for terms.

  • Term: Square Number

    Definition:

    A number that can be expressed as the product of an integer with itself (n²).

  • Term: Perfect Square

    Definition:

    A natural number that is the square of an integer.

  • Term: Square Root

    Definition:

    A value that, when multiplied by itself, gives the original number.

  • Term: Prime Factorization

    Definition:

    Expressing a number as the product of its prime factors.