Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Square Roots
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're going to learn about square roots. Can anyone tell me what a square root is?
Isnβt it the opposite of squaring a number?
Exactly! For example, if we say 4 is a square root of 16, it means that 4 squared equals 16. Let's look at some examples.
What are square numbers?
Good question! Square numbers are those that can be expressed as nΒ², where n is a natural number. So, 1, 4, 9 are examples. Remember the acronym 'SS' for 'Square & Roots' to link squares and their roots!
Can we also find square roots in geometry?
Yes! For instance, if you know the area of a square, you can use square roots to find the side length. We'll practice this in our exercises!
Methods of Finding Square Roots
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let's talk about how to find square roots! We can use repeated subtraction, prime factorization, or the long division method. Which method do you want to start with?
Letβs start with prime factorization!
Great choice! When we do prime factorization, we break down the number into its prime factors. For example, finding the square root of 36 by decomposing it gives us 6 because 36 = 2 Γ 2 Γ 3 Γ 3.
What about the repeated subtraction method?
Good point! This method involves subtracting successive odd numbers until you reach zero. For 81, you subtract 1, then 3, then 5, and so on until you reach zero, finding out the root is 9.
How does the long division method work?
In the long division method, we group digits and find the largest square less than or equal to the dividend. This is a reliable method for larger numbers!
Exercises and Applications
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs put what we've learned into practice! I want each of you to find the square roots of given numbers using the method you prefer.
Can the square root of a number ever be negative?
That's a good observation! While we typically use the positive square root, mathematically, both positive and negative values are correct. For example, both 4 and -4 are square roots of 16.
What if we have a decimal? Can we find its square root?
Yes! We can apply the same principles and even include decimal places in our calculations, like finding the square root of 12.25.
So, if I have a number like 2304, I can find its side as well?
Yes, that's correct! The area of 2304 means we can say the side length is the square root of 2304, which is 48 cm!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the concept of square roots, how to find them using various methods such as prime factorization and the long division method, and their applications in real-world scenarios. Key principles, including the definition of square numbers and their properties, are also outlined.
Detailed
In section 5.5, we delve into square roots, defining them as the inverse operation to squaring a number. Key points covered include:
- The necessity of finding a square root in practical scenarios, such as determining the side of a square from its area.
- Evaluating square roots through different methods: repeated subtraction, prime factorization, and the long division approach.
- The relationship between square numbers and their roots, illustrating that positive square roots are typically what we refer to, though negative roots also exist.
- The importance of understanding square roots in algebra and geometry, with practical examples and exercises designed to reinforce these concepts.
Youtube Videos
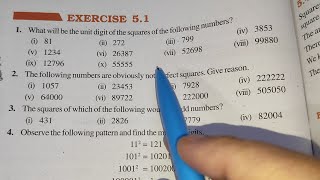
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Square Roots
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Study the following situations.
(a) Area of a square is 144 cmΒ². What could be the side of the square? We know that the area of a square = sideΒ². If we assume the length of the side to be βaβ, then 144 = aΒ². To find the length of the side it is necessary to find a number whose square is 144.
(b) What is the length of a diagonal of a square of side 8 cm? Can we use Pythagoras theorem to solve this? We have, ABΒ² + BCΒ² = ACΒ², i.e., 8Β² + 8Β² = ACΒ²; or 64 + 64 = ACΒ²; or 128 = ACΒ². Again to get AC we need to think of a number whose square is 128.
(c) In a right triangle the length of the hypotenuse and a side are respectively 5 cm and 3 cm. Can you find the third side? Let x cm be the length of the third side. Using Pythagoras theorem 5Β² = xΒ² + 3Β²; 25 - 9 = xΒ²; 16 = xΒ². In all the above cases, we need to find a number whose square is known. Finding the number with the known square is known as finding the square root.
Detailed Explanation
This chunk introduces the concept of square roots through practical scenarios. It discusses how the area of a square and the sides are connected. The area of a square is calculated using the formula: Area = sideΒ². To find the length of the side from the area, we need to perform the reverse operation, which is finding the square root. For example, if the area is 144 cmΒ², we set up the equation 144 = aΒ² and conclude that 'a' must be the square root of 144. Additionally, the chunk highlights using the Pythagorean theorem to find the diagonals or sides of a right triangle by relating the lengths through their squares, emphasizing the importance of finding square roots in various contexts in geometry.
Examples & Analogies
Imagine you have a garden shaped like a square with an area of 144 cmΒ². To plan how many tiles you need to cover that garden, you should know the length of one side. Instead of measuring each side physically, you can find the square root. Itβs like cooking where you have a recipe for a cake that needs a specific pan size; knowing the area helps you find the right size without measuring it every time.
The Concept of Square Roots
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
5.5.1 Finding square roots: The inverse (opposite) operation of addition is subtraction and the inverse operation of multiplication is division. Similarly, finding the square root is the inverse operation of squaring.
We have, 1Β² = 1, therefore square root of 1 is 1. 2Β² = 4, therefore square root of 4 is 2. Since 9Β² = 81, 3Β² = 9, therefore square root of 9 is 3 and (β9)Β² = 81. We say that square roots of 81 are 9 and β9. From the above, you may say that there are two integral square roots of a perfect square number.
Detailed Explanation
In this section, we explore how square roots operate as the inverse of squaring a number. Each number can be expressed as the square of another number. For instance, if we take the number 4, it can be written as 2Β². To find its square root, we determine what number squared gives us 4; in this case, itβs 2. Itβs important to note that perfect squares have two square roots: a positive and a negative (for example, both 9 and -9 are square roots of 81). However, when we refer to the 'square root' in this context, we typically mean the positive root.
Examples & Analogies
Think about a childβs toy box that can be perfectly filled with smaller cubes. If the area of the base of the box is 16 square units and each small cube takes up 1 square unit, knowing the square root helps a child understand how many cubes can fit along one side of the base without the mess of actually stacking and counting each one.
Finding Square Roots through Repeated Subtraction
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
5.5.2 Finding square root through repeated subtraction: Do you remember that the sum of the first n odd natural numbers is nΒ²? That is, every square number can be expressed as a sum of successive odd natural numbers starting from 1. Consider 81. Then, (i) 81 - 1 = 80 (ii) 80 - 3 = 77 (iii) 77 - 5 = 72 (iv) 72 - 7 = 65 (v) 65 - 9 = 56 (vi) 56 - 11 = 45 (vii) 45 - 13 = 32 (viii) 32 - 15 = 17 (ix) 17 - 17 = 0. From 81 we have subtracted successive odd numbers starting from 1 and obtained 0 at 9th step. Therefore 81 = 9.
Detailed Explanation
This section introduces the method of finding square roots by using repeated subtraction of odd numbers. It reiterates that the sum of the first n odd natural numbers equals nΒ², demonstrating this by taking 81 and subtracting odd numbers sequentially until zero is reached. This method effectively shows that it takes 9 steps, corresponding to the number 9, to reach zero from 81, confirming that the square root of 81 is 9.
Examples & Analogies
Picture climbing a stairs where each step represents an odd number. As you count each step starting from 1, when you reach the 9th step (the total distance you travel), you realize youβve covered 81 units; this illustrates how repeated steps can reveal the square root as you subtract each step until you reach the ground.
Finding Square Root through Prime Factorization
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
5.5.3 Finding square root through prime factorisation: Consider the prime factorisation of the following numbers and their squares. By pairing the prime factors, we get. 324 = 2 Γ 2 Γ 3 Γ 3 Γ 3 Γ 3 = (2 Γ 3 Γ 3)Β². Therefore, 324 = 18. Is 48 a perfect square? We know 48 = 2 Γ 2 Γ 2 Γ 2 Γ 3. Since all the factors are not in pairs, 48 is not a perfect square.
Detailed Explanation
This segment of the section focuses on finding square roots through prime factorization, where a number is expressed as a product of prime factors. For example, the number 324 can be factorized into pairs of primes. By grouping the pairs, you find the square root easily, as the square root of a number is derived from its prime factorization by taking one of each pair. This method also helps determine whether a number is a perfect square by checking if prime factors can be paired completely.
Examples & Analogies
Imagine you are sorting colored balls by color and size. You notice that when two balls of the same color and size come together, they form a pair. If you try to complete pairs with all your balls and can couple them perfectly, it symbolizes that you have a perfect square. However, if thereβs a lone ball left without a partner, it indicates that the total number of balls (or your number) isnβt a perfect square, akin to prime factor pairing.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Square Roots: The number which, when squared, gives the original number.
-
Perfect Squares: Numbers that have integer square roots.
-
Calculation Methods: Different ways to calculate square roots including prime factorization and long division.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Finding the square root of 36 results in 6, as 6 Γ 6 = 36.
-
The area of a square with an area of 144 cmΒ² has a side length of 12 cm because 12 Γ 12 = 144.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
To find square roots, look in pairs, break them down, be aware!
π Fascinating Stories
-
Once there was a square named 36 who wanted to find out who its best friend was. After searching, it found out that 6 was the root of its circle of friends!
π§ Other Memory Gems
-
Remember S for Square, R for Root - Square a number, find R for Root.
π― Super Acronyms
SR (Square Root) - Simple Relations in pairs!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Square Root
Definition:
A value that, when multiplied by itself, gives the original number.
-
Term: Square Number
Definition:
A number that can be expressed as the square of an integer.
-
Term: Perfect Square
Definition:
A number whose square root is an integer.
-
Term: Prime Factorization
Definition:
Breaking down a number into its prime components.