Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Free Vibration with Damping
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we'll explore free vibration in damped systems. The equation of motion we look at is mu¨(t) + cu˙(t) + ku(t) = 0. Can anyone tell me what this means?
It describes how a mass oscillates back and forth when disturbed, but what does the damping part do?
Great question! Damping affects how quickly those oscillations die down. In an underdamped system, we see a decaying sinusoidal motion, governed by the damping ratio, ζ.
So, does a higher damping ratio mean the vibrations decay faster?
Exactly! The decay rate is inversely proportional to the damping ratio. If ζ is high, vibrations settle back to rest quickly. Remember this simple rhyme: 'High ζ means bye-bye oscillations quick!'.
What happens if the damping ratio is zero?
In that case, the system is undamped and will oscillate indefinitely. In real life, though, damping is always present!
To recap, free vibrations in damped systems decrease in amplitude over time, and the damping ratio directly affects this rate. Let's move to forced vibrations.
Forced Vibration with Damping
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
In forced vibrations, we're looking at how a system responds to external forces—such as an earthquake. The equation now includes F(t), represented as mu¨(t) + cu˙(t) + ku(t) = F(t). What does that imply?
The system responds to the external force, right? How does it behave over time?
Absolutely! We see a transient response, where the vibration starts to decay, and a steady-state response that continues as long as the force is applied. Like trying to keep a ball bouncing – it eventually stabilizes after being pushed.
So how does forced vibration differ from free vibration?
Great point! Free vibrations are caused by initial conditions, while forced vibrations respond to ongoing applications of force, leading to varying decay based on if the external force persists or ceases.
To sum up, forced vibrations incorporate external forces and show both transient and steady states, illustrating the complex behavior of damped systems under dynamic conditions.
Resonance and Damping Effect
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let’s talk about resonance. Does anyone remember what resonance means?
It's when the frequency of an external force matches the natural frequency of the system, causing bigger oscillations!
Exactly right! But what happens when we add damping to this scenario?
I think it reduces the peak amplitude and makes the system respond more gently, right?
Yes! Damping plays a crucial role in mitigating resonance effects, making structures safer during events like earthquakes. Remember, damping broadens the frequency response, which is beneficial for structural integrity.
So, more damping means less worry during strong shaking?
Exactly! Higher damping decreases the likelihood of damaging oscillations at resonance and is a key design aspect in earthquake engineering.
To conclude today’s discussion, damping enhances the performance of structures during resonant conditions by reducing amplitudes and risks.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section outlines how free vibrations in a damped system decay over time based on the damping ratio, while forced vibrations respond to external dynamic forces, leading to transient and steady-state responses. It also explains how resonance is affected by damping, reducing peak amplitudes and broadening response spectra.
Detailed
In this section, we explore the principles of free and forced vibrations in systems where damping is present. The mathematical representation of free vibrations shows that the equation of motion is governed by the damping ratio: undamped systems resonate indefinitely, while underdamped systems exhibit decaying sinusoidal motions. In context of forced vibrations, when external forces such as earthquakes are applied, the equation of motion includes both transient and steady-state responses. Damping significantly influences resonance behavior, reducing maximum amplitudes and broadening the resonance range. This understanding is crucial in earthquake engineering where proper damping mitigates structural risks during seismic events.
Youtube Videos
![Numerical from past question on basic structural dynamics||Earthquake Engineering|| [Lec-2]](https://img.youtube.com/vi/36ApBVBLxhA/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Free Vibration with Damping
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
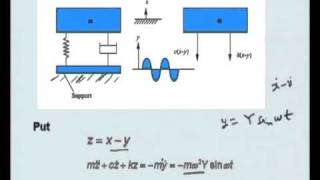
The equation of motion:
mu¨(t)+cu˙(t)+ku(t)=0
Solution depends on the damping ratio:
• Underdamped systems show decaying sinusoidal motion.
• The decay rate is governed by ζ.
Detailed Explanation
This chunk introduces the concept of free vibration in a system that includes damping. The equation of motion describes how a mass behaves when not subjected to external forces but affected by its own momentum and damping. The solution indicates that for a system with low damping (underdamped), the vibrations will decrease over time but still oscillate in a sinusoidal pattern. This oscillation gradually fades away, and the rate at which it fades (the decay rate) is determined by the damping ratio (ζ).
Examples & Analogies
Imagine a swing at a playground. If you give it a push and let it go, it will swing back and forth (vibrate). However, because of air resistance and friction on the swing set (damping), it will gradually slow down until it stops moving. The rate at which it slows down can be thought of as the damping effect.
Forced Vibration with Damping
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When external dynamic forces (e.g., earthquake ground motion) are applied:
mu¨(t)+cu˙(t)+ku(t)=F(t)
The solution includes:
• Transient response (decays with time)
• Steady-state response (sustained due to periodic forcing)
Detailed Explanation
In this chunk, we discuss forced vibrations, where the mass is subjected to external forces such as ground shaking from an earthquake. The equation of motion now includes a term for the external force, F(t), representing the influence of these external factors. The solution to this equation reveals two types of responses: transient response, which fades away over time as the system stabilizes, and steady-state response, which continues indefinitely as long as the periodic forcing is applied. The steady-state response is influenced by the continual external forces acting on the system.
Examples & Analogies
Consider a person on a trampoline jumping up and down. When they jump, they create a force on the trampoline (external force). Initially, as they jump, different responses occur: their bouncing is like the transient response which fades when they stop jumping, while if they keep bouncing at a consistent rhythm, that steady bouncing represents the steady-state response.
Resonance and Damping Effect
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In undamped systems, resonance occurs when the forcing frequency matches the natural frequency. Damping reduces the peak amplitude at resonance and broadens the response spectrum.
Detailed Explanation
This chunk explores the phenomenon of resonance, which happens when the frequency of external forces matches the system's natural frequency. In a system without damping, this can lead to dangerously high oscillations, known as resonance peaks. However, when damping is present, it moderates these peaks, leading to smaller maximum oscillations and a broader range of frequencies over which the system can respond effectively. Hence, damping is crucial in maintaining the safety and stability of structures during dynamic events like earthquakes.
Examples & Analogies
Think of a child on a swing. If you push the swing at the right moment (matching the swing's natural frequency), the child goes really high (resonance). But if you push the swing gently, where the child feels a little less force as the swing moves, the result is a more controlled swing height and less chance of the swing flipping over (the damping effect).
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Free Vibration: Defined as oscillation without external force.
-
Forced Vibration: Defined as response to external forces.
-
Damping Ratio (ζ): Determines decay rates of oscillations.
-
Resonance: Occurs at natural frequency; damping minimizes risks.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An example of free vibration is a child swinging on a swing set, where they keep moving back and forth until naturally slowing down.
-
A great example of forced vibration is a building swaying during an earthquake due to seismic waves impacting it.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Damping lowers sway, keeps the building at bay!
📖 Fascinating Stories
-
Imagine a tightrope walker – the sways they make while trying to balance reminds us of damping, as it helps bring them to a steadier state.
🧠 Other Memory Gems
-
DAMP: Decay against Motion at Pause.
🎯 Super Acronyms
FAD - Free oscillations are damped.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Free Vibration
Definition:
Oscillations that occur in a system when it is disturbed from its equilibrium position without external forces acting on it.
-
Term: Forced Vibration
Definition:
Oscillations that occur in a system due to external forces applied over time.
-
Term: Damping Ratio (ζ)
Definition:
A non-dimensional measure of damping in a system; indicates the response of the system to oscillations and decay rate.
-
Term: Resonance
Definition:
A phenomenon where a system oscillates with large amplitudes at specific frequencies, often leading to failure.