Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Dynamic Excitation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we are discussing dynamic excitation. Can anyone tell me what makes dynamic forces different from static ones?
Dynamic forces change over time, while static forces remain constant.
That's right! Dynamic excitation includes any forces that vary with time and can greatly affect a structure’s performance. Can anyone give me an example of dynamic excitation?
Earthquakes are a prime example!
Exactly! Earthquakes introduce transient and unpredictable loads on structures. This brings us to the next key point: the presence of inertial effects. Student_3, can you explain what inertial effects are?
Inertial effects relate to how the mass of a structure does not allow it to respond instantaneously to changes in forces.
Good explanation! The inertia of a structure becomes significant when exposed to dynamic loads. Remember, we have to use different analytical methods for dynamic excitation compared to static forces. This leads us to our core equation of motion.
Lastly, can someone summarize what dynamic excitation entails?
Dynamic excitation refers to forces that vary over time, such as earthquakes, and involve complex responses because of inertia.
Well summarized! This foundational understanding of dynamic excitation will significantly help as we explore more advanced concepts. Let’s move on to discuss how these forces are applied in real-world scenarios.
Equations of Motion
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let's delve deeper into the equations of motion for dynamic excitation. Who can tell me what the basic equation looks like?
It’s Mu¨(t)+Cu˙(t)+Ku(t)=F(t)!
Correct! Can anyone decipher what each of those terms represents?
M is the mass matrix, C is the damping matrix, K is the stiffness matrix, u(t) is the displacement vector, and F(t) is the time-dependent force vector.
Absolutely right! The equation of motion helps us analyze the effects of dynamic forces accurately. Why do you think understanding these components is vital?
It's essential for predicting how structures will respond to dynamic loads during events like earthquakes.
Exactly! And as we've discussed before, predicting response becomes even more crucial when we consider the possible complex behaviors such as resonance. Student_4, can you define resonance?
Resonance occurs when the frequency of the dynamic load matches the natural frequency of the structure, leading to significantly amplified response.
Well articulated! Understanding these concepts will prepare us for analyzing dynamic behaviors in practical designs.
Applications and Examples
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let’s discuss some applications and examples of dynamic excitation. Can you think of structures that were significantly affected by dynamic loads?
The Bhuj earthquake in 2001 caused a lot of damage to structures that weren’t designed to handle dynamic loads.
Correct! Many buildings collapsed because they were designed solely for static loads. This highlights the need for proper analysis in seismic regions. Student_2, can you name another example?
The Kobe earthquake is another example where structures showed strong dynamic responses.
Exactly! Engineers adapted designs to incorporate more dynamic analysis post-event, learning from previous failures. Now, moving forward, how do you think we can mitigate these risks?
We can use techniques like base isolation to reduce the impact of dynamic loads.
Great thought! By applying methods such as base isolation or damping systems, we can ensure structures are more resilient to dynamic excitations. Remembering these lessons is crucial for future engineering practices.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Dynamic excitation refers to forces that change with time and affect structural integrity significantly during events such as earthquakes. It requires a different analytical approach due to the presence of inertia and time-dependent behaviors, contrasting sharply with static forces that operate under predictable and constant conditions.
Detailed
Detailed Summary
Dynamic excitation is a crucial concept in structural engineering, especially in the context of earthquake engineering. It refers to forces or motions that vary with time, as opposed to static forces which are constant or change very slowly. Dynamic excitation includes a variety of scenarios such as earthquakes, vibrations from machinery, impact loads, and any event that introduces sudden forces to a structure.
Key Characteristics:
- Time-Varying: The loads can change in magnitude, direction, or location, leading to unpredictable responses from structures.
- Inertial Effects: Structures cannot adjust gradually to these loads, so inertia plays a significant role in their response.
- Complex Responses: Response to dynamic loads can involve phenomena such as resonance, where the frequency of excitation matches the natural frequency of the structure, leading to potential failures.
Mathematical Modeling:
The behavior of structures under dynamic excitation is described by the equation of motion:
Mu¨(t)+Cu˙(t)+Ku(t)=F(t)
Where:
- M is the mass matrix,
- C is the damping matrix,
- K is the stiffness matrix,
- u(t) is the displacement vector,
- F(t) is the time-dependent force vector.
This equation accounts for mass, damping, and stiffness effects.
Practical Examples:
Some common examples of dynamic excitations include:
- Earthquakes: Representing the most critical dynamic load on civil structures.
- Machinery Vibrations: Causing structural fatigue over time.
- Impact Loads: Such as vehicle collisions.
- Blast Waves: Resulting from explosions.
- Moving Loads: Like those from trains and vehicles.
In understanding dynamic excitation, engineers can develop robust designs to mitigate these time-dependent effects, emphasizing the importance of advanced analytical methods distinct from static loading considerations.
Youtube Videos
![Lecture 1 Dynamic Loads, Earthquake & Plate Tectonics [Structural Mechanics]](https://img.youtube.com/vi/iAwbw_nKero/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Dynamic Excitation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Dynamic excitation refers to forces or motions that vary with time and involve inertia and damping effects. These excitations may be periodic, transient, or random.
Detailed Explanation
Dynamic excitation is the term used to describe forces that change over time, as opposed to static forces, which remain constant. Examples of dynamic excitations include movements like vibrations or forces that come and go, such as those caused by an earthquake or machinery operation. Key aspects of dynamic excitation are that it involves both inertia—how the structure will behave due to its mass reacting to the force and damping—how the vibrations or movements are reduced over time within the structure.
Examples & Analogies
Think of a bouncing ball. When the ball hits the ground, it does not just drop straight down and stop; it compresses and vibrates, representing dynamic excitation. Just like Earthquakes or machinery causes structures to vibrate and shift, the ball's movements showcase how dynamic forces operate.
Characteristics of Dynamic Excitation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Time-varying: The magnitude, direction, or location of the load changes with time.
• Inertial effects present: Since the structure doesn't have time to adjust gradually, inertia plays a crucial role.
• Complex structural response: The response may include resonance, amplification, and damping.
• Time-domain and frequency-domain analysis required.
Detailed Explanation
Dynamic excitation has several unique characteristics that distinguish it from static forces. Since these forces do not remain constant and can change in intensity and direction, they cause structures to react differently. Inertia, the tendency of an object to resist changes in motion, is significant here because the forces act too quickly for the structure to respond smoothly. As a result, structures can experience complex behavior like resonance and amplification, which can lead to more severe stress and potential damage. To analyze and design structures that can withstand dynamic excitation, engineers use both time-domain and frequency-domain methods, which look at how forces affect structures over time and across different frequencies, respectively.
Examples & Analogies
Imagine how a swing in a playground reacts when you push it. When you push it at just the right time (matching its natural swinging frequency), the swing goes higher and higher due to resonance. This example illustrates how a structure can amplify its response to dynamic forces, similar to how buildings can react during earthquakes.
Examples of Dynamic Excitation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Earthquakes
• Vibrations due to machinery
• Impact loads (vehicle collision)
• Blast and shock waves
• Moving loads (trains, vehicles)
Detailed Explanation
Dynamic excitation can occur in various forms, each producing different types of forces on structures. Earthquakes are one of the most critical forms because they are unpredictable and can cause significant damage to buildings. Machinery can cause vibrations that affect nearby structures, while impact loads, such as a vehicle collision, introduce sudden forces. Additionally, blast and shock waves from explosions create shock effects. Moving loads, like those from trains and vehicles, continually change the forces experienced by structures, making them dynamic in nature.
Examples & Analogies
Consider driving on a bridge. The passing vehicles create shifting loads as they move across the span. This is like a live performance where the presence of every dancer (vehicle) contributes to the overall motion of the stage (bridge), showing the ongoing dynamic nature of forces in action.
Equation of Motion for Dynamic Excitation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The behavior of structures under dynamic excitation is governed by the equation of motion:
Mü(t) + Cu˙(t) + Ku(t) = F(t)
Where:
• M = Mass matrix
• C = Damping matrix
• K = Stiffness matrix
• u(t) = Displacement vector
• F(t) = Time-dependent force vector
Detailed Explanation
The equation of motion is a mathematical expression that describes how structures respond to dynamic forces. It consists of three main components: the mass matrix (M), which accounts for the structure's inertia; the damping matrix (C), which illustrates how energy is dissipated through the structure; and the stiffness matrix (K), which represents the structural resistance to deformation. The displacement vector (u(t)) indicates how far the structure moves in response to applied forces (F(t)) over time. This equation is crucial for engineers to predict how structures will behave when subjected to dynamic forces, guiding safe and effective design.
Examples & Analogies
Think of a trampoline. When you jump on it, your weight is like the mass in the equation, the elastic material of the trampoline represents the stiffness, and how it slows down your bounce showcases the damping. All these factors work together in a mathematical relationship to determine how high you’ll bounce, similar to how engineers use the equation of motion to assess structural behavior.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Dynamic Excitation: Refers to time-varying forces affecting structures, necessitating specific analysis methods.
-
Inertia: A key factor that complicates structural response under dynamic loads, as structures cannot adjust to changes immediately.
-
Resonance: A condition where the frequency of excitation matches a structure's natural frequency, leading to potential failure.
-
Equation of Motion: Mathematical representation of the dynamics of a structure, comprising mass, damping, and stiffness elements.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
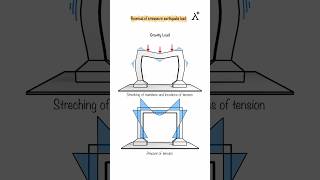
The 2001 Bhuj Earthquake demonstrated the critical impact of dynamic loading and resulted in many structural failures due to inadequate design against dynamic forces.
-
The Kobe Earthquake of 1995 led to many bridges and high-rise buildings demonstrating significant dynamic responses, highlighting the need for energy dissipation strategies.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Dynamic forces sway and shake, with inertia they do make; watch them change, they never rest, structures must be at their best.
📖 Fascinating Stories
-
Once upon a time, in a land prone to earthquakes, a wise engineer designed a tower. He knew that static could not do; he added dampers and isolators too! When the ground shook, the tower performed, and everyone cheered, for its design had transformed!
🧠 Other Memory Gems
-
Remember 'DIRE' for dynamic effects: Dynamic, Inertia, Resonance, and Equation.
🎯 Super Acronyms
DREAM
- Dynamic Response
- Effects of Acceleration
- Mitigation.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Dynamic Excitation
Definition:
Forces or motions that vary with time, affecting the structural response significantly.
-
Term: Inertia
Definition:
The resistance of a structure to change in motion.
-
Term: Resonance
Definition:
A phenomenon where a structure vibrates at a large amplitude due to matching frequencies with applied dynamic loads.
-
Term: Equation of Motion
Definition:
A mathematical equation describing the relationship and effects of mass, damping, and stiffness under dynamic conditions.