Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Static Forces
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today we're discussing static forces. Can anyone tell me what static forces are?
Are they the forces that don’t change over time?
Exactly! Static forces are applied slowly to a structure until they reach full magnitude and then they stay constant. This means they're time-invariant and don't create inertial effects.
What do you mean by inertial effects?
Great question! Inertial effects are the forces that arise because of the mass of the structure and its acceleration. In static conditions, we can neglect these effects because the loads are applied gradually.
So, what kind of examples are we talking about?
Examples include dead loads, like the weight of the structure itself, and live loads, like furniture. All of these are predictable, allowing easier analysis.
How do we calculate these forces?
We primarily use static analysis, which simplifies calculations by assuming equilibrium without considering time. Let's summarize: Static forces are constant, do not have significant inertial effects, and use straightforward static analysis.
Exploring Dynamic Excitation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let’s shift to dynamic excitation. Who can tell me what that means?
Are those the forces that change quickly over time?
Exactly! Dynamic excitation refers to forces or motions that vary with time, such as during an earthquake. They involve both inertia and damping effects.
What does involving inertia mean?
Inertia is significant because the structure cannot adjust gradually to these changes. This leads to complex responses, potentially causing resonance, which we must analyze carefully.
Can you give some examples of dynamic excitation?
Certainly! Common examples include earthquakes, vibrations from machinery, and vehicle impacts. Each requires a different analytical approach—we often use differential equations for dynamic analysis.
And how does this response differ from static?
The response to dynamic forces is transient and can lead to resonant behavior, which isn't typically seen in static loading conditions. Make sure to remember: Dynamic forces are time-dependent, involve inertia, and result in complex structural responses.
Contrasting Static and Dynamic Forces
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let’s compare the two forces. What are the main differences between static and dynamic forces?
Static forces are constant and easy to analyze, while dynamic ones change and are more complex?
Right! And static forces negate inertia effects, while dynamic forces do not, making their analysis substantially different.
Can you break down the types of analysis used?
Sure! We use static analysis for static forces, which is simpler, while dynamic analysis involves complex calculations using differential equations to capture time-dependent effects.
What happens if we treat a dynamic load as a static one?
That's a critical mistake! Treating dynamic loads as static can lead to structural failure since the design wouldn't account for the additional forces and responses. Make sure we've got these differences clear: static forces are constant and predictable, while dynamic forces are time-varying and complex.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
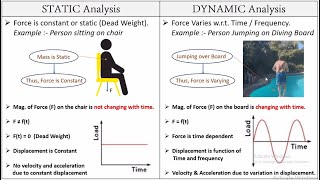
In structural engineering, particularly earthquake engineering, it is critical to understand the differences between static forces and dynamic excitations. Static forces are time-invariant and do not consider inertia, while dynamic excitations vary over time and involve inertial effects. Each type affects structures distinctly, requiring different approaches for analysis and design.
Detailed
Key Differences Between Static and Dynamic Forces
In structural and earthquake engineering, understanding the differences between static forces and dynamic excitations is crucial for impactful design and analysis. Static forces are constant or change slowly over time. These forces, such as dead loads, live loads, and steady wind loads, do not induce significant time-dependent effects, making their analysis relatively straightforward. Dynamic excitation, which includes earthquakes and other time-varying forces, requires a different approach because these forces can change rapidly and introduce inertia effects into the equation, complicating the response of structures.
Key Differences:
- Time Dependency: Static forces remain constant or change slowly, while dynamic forces are rapidly time-varying.
- Inertial Effects: Static forces allow structures to adjust gradually, rendering inertial effects negligible; whereas, dynamic forces significantly impact behavior due to sudden changes.
- Analysis Type: Static analysis involves simpler algebraic equations, while dynamic analysis requires complex differential equations and time-dependent solutions.
- Examples: Static forces include the self-weight of structures, whereas dynamic excitation encompasses earthquake loads and wind gusts.
- Response: Structures under static loading exhibit steady and predictable responses, contrasting with the transient and potentially resonant responses to dynamic loading.
These differences highlight the importance of considering both force types in designing safe, robust structures especially in areas prone to seismic activity.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Time Dependency
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Aspect Static Forces Dynamic Excitation
Time dependency Constant or slowly changing Rapidly time-varying
Detailed Explanation
Static forces are those that are constant or change slowly over time. This means their effects on structures can be predicted easily. On the other hand, dynamic excitation refers to forces that change quickly in magnitude or direction, like those experienced during an earthquake. This time variability makes their behavior less predictable.
Examples & Analogies
Think of how the wind moves differently. A gentle breeze (static force) may just sway a tree lightly, while a sudden gust (dynamic force) can bend it significantly. Just like the tree, structures respond differently depending on whether the force they experience is constant or rapidly changing.
Inertial Effects
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Inertial effects Negligible Significant
Detailed Explanation
With static forces, the structure can adjust slowly, so the effects of inertia—how mass resists changes in motion—are minimal and often ignored. Conversely, dynamic loads involve rapid changes, making inertia a crucial factor in the analysis. This means the mass of the structure and how it reacts under acceleration must be considered in dynamic scenarios.
Examples & Analogies
Consider riding a bicycle. When you pedal steadily (static situation), it’s easy to balance. But if you suddenly accelerate (dynamic situation), you feel a jolt that can throw you off balance. In structures, this is similar; sudden forces can cause them to sway or vibrate significantly due to their inertia.
Analysis Type
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Analysis type Static analysis Dynamic/time-history/response spectrum analysis
Detailed Explanation
Static analysis involves simpler calculations that assume forces remain constant or change slowly, allowing engineers to predict responses based on equilibrium. Dynamic analysis, however, is more complex. It requires methods to account for the time-varying nature of loads, analyzing how forces change over time and how they affect movement in structures.
Examples & Analogies
Imagine planning a road trip. If you calculate based on a steady speed (static analysis), it’s straightforward. But if you factor in traffic lights, road conditions, or detours (dynamic analysis), your planning becomes much more complicated. Engineers face similar challenges when analyzing structures under dynamic loading.
Mathematical Complexity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Mathematical complexity Simple algebraic equations Differential equations
Detailed Explanation
The mathematical requirements for static forces are relatively straightforward, often involving basic algebraic equations to determine forces and stresses. Dynamic forces, however, involve differential equations that can capture changes over time, reflecting the complexity of how forces vary and interact with structures dynamically.
Examples & Analogies
Consider calculating the area of a rectangle (static) versus modeling how a bouncing ball moves (dynamic). The area is simply length times width (simple equation), whereas the ball's movement involves understanding the changing speed, direction, and forces acting on it (complex equations).
Examples
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Examples Dead loads, live loads Earthquake loads, wind gusts
Detailed Explanation
Common examples of static forces include dead loads, like the weight of the building materials themselves, and live loads, such as people and furniture. Dynamic forces include events such as earthquakes and sudden wind gusts, which apply varying loads to structures unexpectedly.
Examples & Analogies
Think of a bookshelf. The weight of the books (static forces) doesn't change often, making it predictable. But if someone bumps into the shelf or if it’s windy (dynamic forces), the load shifts abruptly. This unpredictability is what structures must be designed to handle in real-world scenarios.
Response Characteristics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Response Steady-state, predictable Transient, possibly resonant
Detailed Explanation
Under static loading conditions, the response of structures is predictable and stable. However, dynamic loads can result in transient responses, where the reactions of the structure change suddenly, and can cause resonant effects, amplifying movements unpredictably.
Examples & Analogies
Imagine a calm lake (static response) versus a lake during a storm (dynamic response). The calm lake’s surface remains smooth, while the storm creates waves that can crash unpredictably against the shore. Structures, like lakes, have predictable behaviors under certain conditions but can react wildly when faced with dynamic forces.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Time Dependency: The rate at which forces vary over time differs between static and dynamic forces.
-
Inertia: Static forces allow adjustments without significant inertia, while dynamic forces require consideration of these effects.
-
Analysis Types: Static and dynamic analyses differ greatly in complexity and methodology.
-
Response Characteristics: The response of structures differs vastly between static and dynamic loading scenarios.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Dead loads, such as the weight of walls or roofs in a building.
-
Dynamic loading examples include earthquakes, which can fluctuate unpredictably.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Static remains, like a rock, while dynamic flows like a ticking clock.
📖 Fascinating Stories
-
Imagine a structure built strong for heavy furniture; that’s static. Now put it on a shaking ground; that’s dynamic, needing more than just brute force.
🧠 Other Memory Gems
-
S.A.I.R. for Static Analysis: Steady, Always, Invariant, Reliable.
🎯 Super Acronyms
D.I.R.E. for Dynamic
- Dynamic
- Inertia
- Response
- Excitation.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Static Forces
Definition:
Forces that remain constant over time or change gradually without causing rapid response effects.
-
Term: Dynamic Excitation
Definition:
Forces or motions that vary over time, leading to significant inertial effects and requiring complex analysis.
-
Term: Inertial Effects
Definition:
Forces experienced by a structure due to its mass and the accelerations applied to it.
-
Term: Static Analysis
Definition:
A method of analyzing structures under static loads, wherein equilibrium conditions are assumed.
-
Term: Dynamic Analysis
Definition:
A complex analysis that accounts for time-varying forces and inertial effects.
-
Term: Resonance
Definition:
A phenomenon where dynamic loading matches a structure’s natural frequency, leading to significant amplification of motion.