Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Ground Motion
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today we're discussing how structures respond when the ground underneath them moves, especially during earthquakes. Can anyone explain what ground motion refers to?
Ground motion is the displacement of the ground, usually due to seismic activity.
Exactly! Ground motion is a critical factor that we must consider in structural dynamics. It can be modeled as a function, usually denoted as $u_g(t)$, where $t$ represents time. Student_2, can you tell me why understanding this motion is vital for our calculations?
It’s important because it helps predict how the structure will behave and what forces we need to design against.
Right. If the structure is moving with the ground, we must account for both its absolute and relative motions. Remember the equation $u_a(t) = u(t) + u_g(t)$? This relationship helps us define these motions better.
So, that means $u(t)$ is the relative motion of the mass, and $u_a(t)$ is the absolute motion?
Exactly! In this context, $u(t)$ becomes our focus for deriving the equation of motion under base excitation.
To sum up, understanding ground motion is fundamental when analyzing the response of structures to seismic forces. We need to consider how the mass behaves relative to the base.
Deriving the Equation of Motion
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
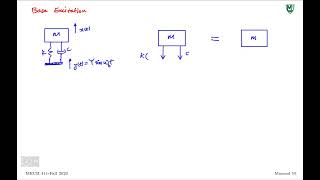
Now, let’s focus on deriving the equation of motion for a mass subjected to base excitation. Can we start with a free body diagram of the mass?
Sure! We have a mass $m$, and it experiences forces from the spring, damper, and the pseudo-force due to ground acceleration.
Exactly! The forces acting on the mass can be summarized as $mu¨(t) + cu˙(t) + ku(t)$. But wait, we must also consider the ground acceleration $-mu¨_g(t)$ which appears on the right side of our equation. Who can explain why we treat this as a pseudo-force?
Because the mass is effectively resisting the motion caused by ground acceleration, we treat it as if there’s a force acting on it.
Correct! Hence, our complete equation of motion becomes $mu¨(t) + cu˙(t) + ku(t) = -mu¨_g(t)$. This shows that our structural response is reliant on both the inherent properties of the structure and the characteristics of the ground motion.
This equation helps engineers understand how the seismic forces impact the structure’s safety, right?
Absolutely! By comprehending this equation, engineers can design buildings to withstand seismic loads more effectively.
In summary, we derived a crucial equation which illustrates how base excitation influences the dynamics of our structural system.
Application and Importance of Derived Equations
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we've derived the equation of motion for our SDOF system, let's discuss its applications. What do you think is the importance of this equation in engineering?
It allows engineers to predict how buildings will respond during an earthquake, helping to ensure safety.
Yes! And it’s crucial for designing structures that can accommodate the forces generated by seismic activities. Understanding this equation helps optimize damping and stiffness in our designs.
So, a well-designed equation will lead to better stability during earthquakes?
Exactly! There’s a direct relationship between the derived equations and structural integrity during seismic events. Remember, a critical aspect is to minimize the relative displacements as they reflect the structural deformation. Let's recap: we derived an equation of motion accounting for base excitation and highlighted its significant role in ensuring safe and resilient structures.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the dynamics of a mass attached to a moving base under seismic excitation are analyzed. The equation of motion is derived using free body diagram analysis, illustrating how the pseudo-force due to ground acceleration affects the system.
Detailed
Derivation of Equation of Motion for Base Excitation
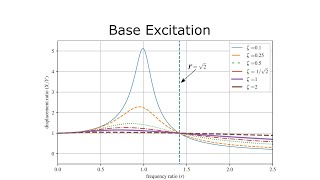
In the analysis of structures subjected to seismic events, understanding the motion of structures relative to a moving base is crucial. This section begins by analyzing the free body diagram of an SDOF system, where the ground motion is represented as a displacement function, $u_g(t)$. The objective is to derive the equation governing the relative motion of the mass. By considering the dynamic behavior of the mass subject to the acceleration of the ground, we arrive at the following governing equation:
$$mu¨(t) + cu˙(t) + ku(t) = -mu¨_g(t)$$
Here, the right-hand side represents a pseudo-force acting on the mass due to ground acceleration, indicating that seismic excitation affects the system like an inertial force. Understanding this derivation is vital for engineers in assessing the performance and safety of structures during earthquakes.
Youtube Videos
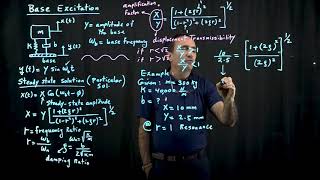
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Free Body Diagram Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Consider the structure's base moving with ground motion u g(t).
Detailed Explanation
In this first step of analyzing the motion for base excitation, we start by recognizing that the base of the structure moves in response to ground shaking. The term 'u g(t)' refers to this movement, where 'u g' signifies the ground displacement over time. It's essential to visualize this movement to understand subsequent dynamic responses. This setting is crucial, as it establishes the foundation for analyzing how structures react to ground accelerations during an earthquake.
Examples & Analogies
Imagine standing in a car as it drives over bumps. Just as the car’s motion affects how you experience those bumps relative to the ground, a building's response during an earthquake depends on how its base moves compared to the ground shaking beneath it.
Governing Equation of Motion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The relative motion u(t) of the mass with respect to base is governed by:
mu¨(t)+cu˙(t)+ku(t)=−mu¨(t)
g
Detailed Explanation
Here, we introduce the governing equation for the motion of the mass in relation to the moving base. The left side of the equation illustrates the mass, damping, and stiffness forces acting upon the mass. The right side shows the influence of the base motion, represented as a pseudo-force resulting from ground acceleration ('-mu¨(t)'). This equation encapsulates how an earthquake can increase the effective inertial force on the building by considering both the base movement and the mass's response.
Examples & Analogies
Think of a child on a swing. If the swing moves (like the base during an earthquake), the child's relative motion (how they move compared to the ground) changes. The swing's acceleration affects how strongly the child feels pushed back – this is similar to how the ground’s movement alters the forces acting on the mass in the structure.
Interpretation of the Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The RHS is a pseudo-force due to ground acceleration.
This equation shows that seismic excitation acts as an inertial force.
Detailed Explanation
The interpretation of the equation highlights that the right-hand side represents an inertial force induced by the motion of the ground. This pseudo-force arises because when the base accelerates downward in an earthquake, the inertia of the mass creates additional forces acting on it. Recognizing this helps us understand the dynamic interactions at play during seismic events and emphasizes the importance of considering ground motion when analyzing structural response.
Examples & Analogies
Imagine being on a trampoline. As someone jumps on one end, you feel a force pulling you upwards and towards the center (like the pseudo-force here). This dynamic is similar to how ground motion creates added forces on a structure that engineers must account for in design.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Base Motion: The motion of the ground often modeled in seismic analysis, crucial for understanding structural response.
-
Equation of Motion: A mathematical representation that describes the dynamics of a system subjected to external forces.
-
Relative and Absolute Motion: Key distinctions in analyzing structural responses where relative motion involves the behavior of the structure concerning the base.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: Consider a building where the ground starts shaking during an earthquake. The base excitation can be modeled as acceleration $u_g(t)$ acting on the building's foundation.
-
Example 2: An SDOF system being subject to ground motion can be analyzed with the equation $mu¨(t) + cu˙(t) + ku(t) = -mu¨_g(t)$, showing how the mass reacts to the ground's influence during seismic events.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When the ground starts to sway,
🧠 Other Memory Gems
-
$mu¨ + c u˙ + ku = -mu¨_g$, hooray!
📖 Fascinating Stories
-
Imagine a mass on a spring in a house. When the earth shakes, the house moves up and down, causing the mass to feel a push down because of the ground’s sway. This helps us see how much the building needs to stand firm against earthquakes.
🧠 Other Memory Gems
-
Remember R.E.G. for seismic analysis: R for Relative motion, E for Earth shaking, and G for Ground influence.
🎯 Super Acronyms
M.E.S.H. for the equation components
- M: for Mass
- E: for External force
- S: for Spring
- H: for Damping.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Base Excitation
Definition:
The motion of the ground that induces vibrations in a structure, causing it to respond to seismic activity.
-
Term: Pseudoforce
Definition:
An imaginary force introduced in the equation of motion due to the acceleration of the ground.
-
Term: Relative Motion
Definition:
The motion of a mass relative to its base or reference point.
-
Term: Absolute Motion
Definition:
The total motion of a mass, taking into account its motion relative to the ground.