Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Seismic Excitation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we are discussing seismic excitation, which is when the ground moves during an earthquake.
So, does that mean the building moves with the ground?
Exactly! The ground movement causes the base of the structure to move. We refer to this as base excitation.
How do we measure the movement of the ground?
Great question! We use the term **ground displacement** to describe how far the ground moves; we denote this as u_g(t).
And how does that relate to the mass of the building?
The mass's movement relative to the ground is the **relative displacement** u(t). The total movement, including that of the ground, is called **absolute displacement**, denoted as u_a(t) = u(t) + u_g(t).
So, absolute displacement accounts for both movements?
Correct! Understanding these relationships is crucial for analyzing how buildings react during seismic events. Let's recap: ground displacement is u_g(t), relative displacement is u(t), and absolute displacement is u_a(t).
Base Excitation vs. Mass Excitation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's differentiate between base excitation and mass excitation.
What’s mass excitation, exactly?
Mass excitation occurs when forces act directly on the mass, like wind loads. In contrast, during an earthquake, the excitation is through base motion.
And why is understanding these concepts important for engineers?
Engineers need to design structures that can withstand the forces experienced during earthquakes, which requires a clear grasp of how ground motion affects structural response.
Is there a way to calculate how much the structure moves?
Yes! We derive equations of motion considering the base's acceleration as a pseudo-force acting on the structure.
So, it treats ground acceleration like an extra force?
Exactly! This approach is essential for predicting the structural behavior during an earthquake.
Applications in Earthquake Engineering
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
How do we apply our understanding of base excitation in real-world engineering design?
I think we use it to improve the safety of buildings?
Correct! By modeling how structures respond to base motions, we can ensure they can safely absorb and dissipate seismic energy.
What tools do engineers use for this analysis?
Typically, engineers employ software that can simulate ground motion and evaluate the structural response accurately.
What about complex buildings with multiple levels?
In those cases, while we start with Single Degree of Freedom models, more complex analysis like Multi-Degree of Freedom systems might be necessary to capture all effects.
So, we have to consider both base and mass excitations when designing?
Absolutely! It’s key for making structures resilient to seismic events. Let's summarize: understanding displacement types and their interactions is crucial for effective design.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Seismic excitation refers to the ground motion experienced during an earthquake, which affects the base of a structure rather than applying forces directly on the mass. This section introduces key terms such as ground displacement and relative motion, and explains the implications for engineering design and analysis.
Detailed
Seismic Excitation as Base Motion
In the context of earthquake engineering, seismic excitation describes the dynamic behavior of structures during an earthquake, where ground movement is transmitted to the base instead of exerted directly on the mass.
Key Concepts:
- Ground Displacement: Denoted as u_g(t), this refers to the movement of the ground.
- Relative Displacement: Represented as u(t), it reflects the movement of the mass concerning the moving base.
- Absolute Displacement: Calculated as u_a(t) = u(t) + u_g(t), this combines the relative and ground displacements.
Understanding these terms is crucial for structural analysis and engineering design. It allows engineers to model the behavior of structures under seismic loading accurately, ensuring that the design can withstand such dynamic forces.
Youtube Videos
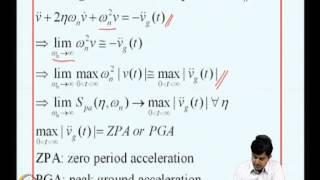
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Base Motion During Earthquakes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
During an earthquake, the ground itself moves, and hence the excitation is applied at the base of the structure rather than on the mass. This is modeled as base excitation.
Detailed Explanation
This chunk introduces the concept of base motion but emphasizes how structures react differently during earthquakes. Unlike normal conditions where forces may act on a building's mass, during an earthquake, the whole base moves with the ground. Therefore, instead of the force being applied directly to the structure (mass excitation), it originates from the base's movement.
Examples & Analogies
Imagine a car driving on a bumpy road. If your body is inside the car and the bumps move the entire vehicle, you feel the motion in your seat, much like how a building experiences base motion during an earthquake. If the bumps happen, that’s the ground's motion affecting the car (your structure).
Key Concepts of Base Excitation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
6.5.1 Concept of Base Excitation
- Ground displacement: u g(t)
- Relative displacement of mass with respect to the base: u(t)
- Absolute displacement: u a(t)=u(t)+u g(t)
Detailed Explanation
This chunk outlines the fundamental concepts related to base excitation. It defines three types of displacements: 'ground displacement' refers to how much the ground moves (represented as u_g(t)), 'relative displacement' indicates how much the mass of the structure moves concerning the moving base (u(t)), and 'absolute displacement' combines both the structure's motion and the ground's motion (u_a(t)). This understanding is crucial for engineers to analyze and design structures that can withstand seismic forces effectively.
Examples & Analogies
Think of a balloon floating in the air with someone shaking the floor. The ground shaking is like the ground displacement (u_g(t)). The balloon moves but not in the same way. The distance between the balloon's position and the shaking floor shows the relative displacement (u(t)). Finally, if you measure where the balloon is regarding the starting point before the shaking started, you get the absolute displacement (u_a(t)).
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Ground Displacement: Denoted as u_g(t), this refers to the movement of the ground.
-
Relative Displacement: Represented as u(t), it reflects the movement of the mass concerning the moving base.
-
Absolute Displacement: Calculated as u_a(t) = u(t) + u_g(t), this combines the relative and ground displacements.
-
Understanding these terms is crucial for structural analysis and engineering design. It allows engineers to model the behavior of structures under seismic loading accurately, ensuring that the design can withstand such dynamic forces.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
During an earthquake, if the ground shakes upward by 3 inches, and the mass also moves up by 2 inches, the absolute displacement is 5 inches.
-
In an earthquake-prone area, buildings must be designed considering base excitation to prevent failure.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When the quake makes the ground shake, buildings rock, but mustn't break.
📖 Fascinating Stories
-
Imagine a tree on a hillside during an earthquake; the ground shakes, but the tree stands tall because it knows how to sway with the wind, just like buildings must learn to move during quakes.
🧠 Other Memory Gems
-
Remember 'GRAB' - Ground motion, Relative motion, Absolute motion, and Building response.
🎯 Super Acronyms
DRA - Displacement, Relative, Absolute - for remembering displacement types.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Seismic Excitation
Definition:
Dynamic forces applied to a structure due to ground motion during an earthquake.
-
Term: Ground Displacement
Definition:
Movement of the ground during an earthquake, denoted as u_g(t).
-
Term: Relative Displacement
Definition:
Movement of the structure's mass relative to the moving ground, represented as u(t).
-
Term: Absolute Displacement
Definition:
Total movement of the mass including ground motion, calculated as u_a(t) = u(t) + u_g(t).