Forced Vibration due to External Force (Mass Excitation)
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Forced Vibration and Equation of Motion
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today we're going to explore forced vibrations in Single Degree of Freedom systems, beginning with the equation of motion. Can anyone tell me what dynamic forces we might encounter in civil engineering?

I think of things like wind or impact loads.

Exactly! These are examples of external forces acting on structures. The governing equation for mass excitation can be expressed as μu¨(t) + cu˙(t) + ku(t) = F(t). Here, what does each component represent?

Mass, damping, and spring stiffness, I think.

Right! Each term plays a critical role in dictating how the system responds to external forces. Remember: MKS for mass, F for force, and k for stiffness. Very useful to categorize!

So, what happens to the system if we don't have damping?

Good question! The system would oscillate indefinitely with its natural frequency, leading to possibly destructive resonance. Now, let's dive deeper into various solution methods.
Methods of Solution for Forced Vibration
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

To solve for the system’s response under mass excitation, we have several methods. Can someone name a few?

Maybe the classical method and the Laplace transform?

Exactly! Duhamel’s integral is part of the classical method. It's powerful for arbitrary forcing functions. Has anyone used Laplace transforms before?

Yes! It helps simplify differential equations into algebraic ones.

Exactly! And it’s particularly helpful for analyzing the response of systems to forced vibrations. Let's summarize this key point: both Duhamel’s integral and Laplace transforms help in finding time-dependent solutions for our equations.
Response to Harmonic Loading
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s consider a harmonic force applied to the system described by F(t) = F₀sin(ωt). How do we expect our system to respond?

Wouldn't the response also be sinusoidal?

Exactly! The steady-state response is characterized by amplitude and phase angle. Can anyone tell me the significance of resonance in this context?

Resonance occurs when the frequency matches the natural frequency, which can cause large oscillations.

Well done! The condition for resonance, ω ≈ ωn, signifies that engineers must design structures to prevent such conditions. Remember this phrase: 'Resonance is the dance of vibrations.'
Practical Applications of Forced Vibration Analysis
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

In practice, understanding these principles helps us design safer structures. Can someone provide an example of where this applies?

Maybe during an earthquake, when the ground movement impacts buildings?

Absolutely! Earthquakes create dynamic forces that can resonate buildings. It's crucial to analyze them using our established equations. Why is it important to accurately model damping?

Because it affects the response and potential damage to the structure.

Exactly! Remember: Damping is our safety feature to reduce dynamic responses. For practice, we will explore a case study to solidify your understanding.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we explore the dynamics of forced vibration in an SDOF system when an external force is applied. We derive the equation of motion, introduce solution methods such as classical, Laplace, and numerical methods, and analyze the response to harmonic loading, including conditions for resonance.
Detailed
Forced Vibration due to External Force (Mass Excitation)
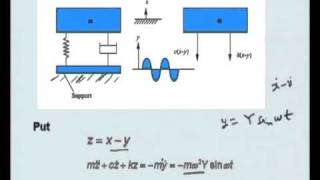
In this section, we analyze the dynamics of a Single Degree of Freedom (SDOF) system subjected to an external force. The governing equation of motion can be expressed as:
Equation of Motion:
m * u¨(t) + c * u˙(t) + k * u(t) = F(t)
Where:
- m is the mass of the system,
- c is the damping coefficient,
- k is the spring constant,
- u(t) is the displacement,
- F(t) is the applied external force.
6.4.1 Equation of Motion for External Force
- The applied force F(t) directly affects the motion of the system, making this analysis crucial.
- Common methods of solution include:
- Classical methods such as Duhamel’s integral,
- Laplace transform techniques,
- Fourier Transform,
- Numerical methods like the Newmark-beta method.
6.4.2 Response to Harmonic Loading
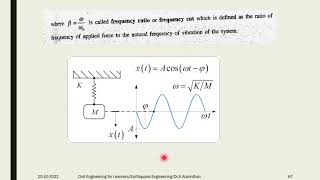
- When the external force is harmonic, described as F(t) = F₀ * sin(ωt), the system's steady-state response can be derived.
- The steady-state displacement response is given by:
- u(t) = U * sin(ωt − ϕ), where U represents the amplitude of the response and ϕ is the phase angle.
- Resonance occurs when the frequency of the external load ω approaches the natural frequency of the system ωn, potentially amplifying the response.
Understanding forced vibration due to external forces is critical for safer and more resilient structural engineering designs.
Youtube Videos







Audio Book
Dive deep into the subject with an immersive audiobook experience.
Equation of Motion for External Force
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Applied Force: F(t)
Equation:
mu¨(t)+cu˙(t)+ku(t)=F(t)
Methods of Solution:
- Classical method (Duhamel’s integral)
- Laplace transform
- Fourier Transform
- Numerical methods (e.g., Newmark-beta)
Detailed Explanation
This chunk introduces the concept of forced vibration due to an external force acting on a single degree of freedom (SDOF) system. The equation of motion describes how the system responds when a force F(t) is applied. The left side of the equation mu¨(t)+cu˙(t)+ku(t) represents the dynamics of the system, with m being mass, c being damping, and k being stiffness. The equation can be solved using various methods:
1. Classical method (Duhamel’s integral): A traditional analytical approach.
2. Laplace transform: A technique used to convert differential equations into algebraic equations, simplifying the solution process.
3. Fourier Transform: Useful for solving equations with periodic forcing functions.
4. Numerical methods (e.g., Newmark-beta): Approaches that allow for approximate solutions, especially useful for complex systems where analytical solutions are infeasible.
Examples & Analogies
Imagine a swing pushed by a person (the external force) as it oscillates back and forth. The swing's motion, influenced by its weight, the push from the person, and any air resistance acting on it, can be similarly described by an equation of motion just like the SDOF system. This interaction reflects how forces affect the dynamics of the swing, paralleling the concepts in forced vibration analysis.
Response to Harmonic Loading
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Applied force: F(t)=F 0sin(ωt)
Steady-state solution:
u(t)=Usin(ωt−ϕ)
where U= 0 , and ϕ is the phase angle.
Resonance condition: ω≈ω n
Detailed Explanation
In this chunk, we examine how the SDOF system responds when subjected to harmonic loading, which is a force that varies sinusoidally with time, expressed as F(t)=F 0sin(ωt). The resulting steady-state solution indicates how the system behaves over time, represented by u(t)=Usin(ωt−ϕ), where U corresponds to the amplitude of motion and ϕ indicates the phase relationship between the force and the mass’s response. It's important to note the resonance condition, which occurs when the frequency of the applied force ω is close to the natural frequency of the system ω n, leading to significantly amplified vibrations.
Examples & Analogies
Consider the example of a child on a swing. If someone pushes the swing at a rhythm matching the swing's natural back-and-forth motion (its natural frequency), the swing will go higher (resonance). Conversely, if they push at an irregular tempo, the swing won’t gain the same height. This is analogous to how a structure resonates with certain frequencies when subjected to forces.
Key Concepts
-
Equation of motion: Describes how systems respond to dynamic loads.
-
Response to harmonic loading: Systems behave sinusoidally under periodic forces.
-
Resonance: Critical condition when frequency matches natural frequency.
Examples & Applications
A building subject to wind loads exemplifies forced vibrations.
A suspended mass on a spring oscillates when subject to an external periodic force.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When forces align to cause great sway, vibrations dance in a wild ballet.
Stories
Imagine a guitar with strings. When strummed, if the notes match the guitar’s natural frequency, it vibrates louder than normal, illustrating resonance.
Memory Tools
Remember 'FRD' - Forces, Resonance, and Damping for forced vibrations.
Acronyms
M.E.R. - Mass, Excitation, Resistance for remembering key concepts.
Flash Cards
Glossary
- Forced Vibration
Vibrations occurring in a system due to external forces.
- Mass Excitation
Excitation applied directly to the mass of a structure.
- Equation of Motion
Mathematical representation of motion, derived from Newton’s Laws.
- Resonance
Amplification of response when the frequency of excitation matches the system's natural frequency.
- Harmonic Loading
A periodic external force applied to a system.
Reference links
Supplementary resources to enhance your learning experience.
