Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
What is Damping?
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will explore the concept of damping in vibratory systems. Can anyone tell me what damping refers to?
Is it related to reducing movement or vibrations in structures?
Exactly! Damping is the mechanism through which vibrational energy is dissipated, helping to reduce motions in structures. It’s essential for preventing damage in events like earthquakes. We can remember this with the acronym 'DAMP'—Dissipating Amplitude of Motion. What are some sources of damping that you can think of?
Would internal material friction count as a source?
Yes, that’s correct! Other sources include friction at joints, air resistance, and energy-absorbing devices.
Why is damping so important in structural engineering?
Great question! It limits the vibrations that occur due to dynamic forces, especially important during earthquakes. In fact, proper damping can save lives and structures!
Can we represent damping mathematically?
Absolutely! Damping is represented by the equation F = c⋅x˙, which links the damping force to the damping coefficient and the velocity of motion. Remember this equation; it's fundamental.
To summarize, damping helps reduce vibrations and is vital in maintaining structural integrity, particularly during seismic events.
Sources of Damping
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let’s discuss the various sources of damping. Can you recall any of them?
Air resistance and internal friction?
Correct! Air resistance and internal material friction are important. Let’s break them down. Air resistance occurs when an object moves through air, and this resistance helps dissipate energy. What about internal material friction?
That’s when the molecules in a material move against each other, right?
Yes, exactly! Internal material friction generates heat, which is a form of energy dissipation. Moving on, friction at joints also plays a critical role. It often absorbs energy in structures with connections.
And what about energy-absorbing devices?
Good catch! These are specifically designed to dissipate energy, and they can be integrated into structures to enhance damping further. Can anyone think of an application where this might be critical?
In buildings during earthquakes?
Absolutely! By using energy-absorbing devices and understanding damping, we can significantly enhance a building's resilience to seismic actions. Remember, the more we understand energy dissipation, the better we can create safe structures.
Mathematical Representation of Damping
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let’s delve into the mathematical representation of damping. Who remembers the equation for damping force?
It’s F = c⋅x˙?
Correct! In this equation, **F** represents the damping force, **c** is the damping coefficient, and **x˙** is the velocity of the moving mass. Why do you think it matters to express damping this way?
It helps quantify how much damping is present in a system?
Exactly! This quantification is crucial for engineers to design systems effectively. When we know how damping behaves in a system, we can predict how that system will react to dynamic loads.
So, the damping coefficient tells us how effective the damping is?
Yes, that’s right! A higher **c** means more energy dissipation, which is preferable in many scenarios. Does anyone want to explore how this formula applies in real-world scenarios?
Like in designing earthquake-resistant buildings?
Exactly! Adjusting the damping coefficient allows engineers to optimize designs for specific conditions. Remember, damping impacts both safety and performance.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section introduces the concept of damping in vibratory systems, explaining how various sources of damping—such as internal material friction, air resistance, and mechanical devices—help dissipate vibrational energy and restore systems to rest after excitation. The section emphasizes the importance of understanding damping in seismic design for civil engineers.
Detailed
Concept of Damping in Vibratory Systems
Damping refers to the mechanism by which energy is dissipated in a vibrating system, effectively reducing the amplitude of vibrations and aiding in the system's return to rest after being excited. In real-world applications, various factors contribute to damping, including:
- Internal material friction: Resistance within the material that generates heat and dissipates energy.
- Friction at joints: Energy loss due to frictional forces at points of connection.
- Air resistance: Damping effects incurred when a body moves through air, leading to energy loss.
- Energy-absorbing devices: Devices designed to intentionally absorb and dissipate vibrational energy.
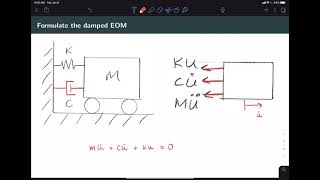
Mathematically, damping introduces a damping force into the equations of motion represented as:
$$F = c \cdot \dot{x}$$
Where:
- F = damping force
- c = damping coefficient
- \dot{x} = velocity
Understanding the different types of damping and how they apply is essential for civil engineers, particularly when designing structures that need to withstand dynamic loads, such as those encountered during earthquakes.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Damping
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Damping is the mechanism by which energy is dissipated in a vibrating system. It reduces the amplitude of vibrations and brings the system back to rest after excitation.
Detailed Explanation
Damping is a process that helps in controlling vibrations in systems that are disturbed from their rest position. When a structure vibrates due to external forces, it possesses a certain amount of energy which manifests as oscillation. Damping works by dissipating this energy, thereby reducing the height of the vibrations (amplitude) and eventually bringing the system back to its original position (rest) after it has been excited.
Examples & Analogies
Think of damping like a car's suspension system. Just as the shocks and struts absorb bumps on the road and keep the ride smooth, damping in a structure helps it move less violently during events such as earthquakes, making it safer.
Sources of Damping
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In real-world structures, damping comes from:
- Internal material friction
- Friction at joints
- Air resistance
- Energy-absorbing devices
Detailed Explanation
Damping in structures can come from several sources. Internal material friction occurs when the particles in a material rub against each other during deformation. Friction at joints refers to the resistance encountered at connections between structural elements. Air resistance is caused by the movement of the structure through the air, while energy-absorbing devices are specifically designed tools that help in reducing vibrations, such as dampers or shock absorbers.
Examples & Analogies
Imagine you're riding a bicycle on a bumpy path. The friction between the tire and the ground, the air pushing against you as you pedal, and the way your body absorbs the jolts when going over bumps are all forms of damping. Just as these factors help control your ride, damping in structures helps manage how they respond to forces.
Mathematical Representation of Damping
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Mathematically, damping is introduced into the equations of motion through a damping force, usually proportional to velocity, represented as:
F = c ⋅ x˙
Where:
- F = damping force
- c = damping coefficient
- x˙ = velocity
Detailed Explanation
In mathematical terms, damping is expressed using a formula that relates the damping force to the speed at which an object is moving. The damping force (F) is proportional to the velocity (x˙) and is influenced by a factor called the damping coefficient (c), which quantifies how much resistance there is to the motion. This relationship helps engineers understand and predict how a structure will behave when subjected to dynamic forces.
Examples & Analogies
Think of damping like applying brakes to a moving car. The faster the car moves (higher velocity), the more braking force is needed to slow it down. Similarly, in damping, the faster something vibrates, the more damping force there is to reduce that motion.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Damping: A mechanism to dissipate vibrational energy in structures.
-
Damping Coefficient: A measure of how effectively damping reduces motion.
-
Damping Force: Opposes the motion, crucial in equations of motion.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Internal friction within a beam under stress generates heat and dissipates energy.
-
Air resistance experienced by a high-rise building during strong winds reduces potential sway.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Damping keeps our structures safe, it calms the tremors in their place.
📖 Fascinating Stories
-
Once, in a city prone to disturbances, engineers learned to deploy dampers, like shields, surrounding buildings, softening the blows of earthquakes.
🧠 Other Memory Gems
-
D.A.G.E. - Damping, Absorbing, Generating, Energy loss.
🎯 Super Acronyms
DAMP - Dissipating Amplitude of Motion.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Damping
Definition:
The process by which vibrational energy is dissipated, reducing the amplitude of motion in systems.
-
Term: Damping Coefficient (c)
Definition:
A parameter in the damping force equation representing the effectiveness of damping.
-
Term: Damping Force (F)
Definition:
The force that opposes motion, proportional to velocity and defined mathematically as F = c⋅x˙.